7. Анализ устойчивости по критерию Найквиста

Согласно критерию Найквиста, если система устойчива в разомкнутом состоянии, то для устойчивости соответствующей замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы при изменении частоты от 0 до ¥ не охватывала точку (—1;j0) на комплексной плоскости.

Для построения годографа в передаточной функции разомкнутой системы заменим S на , получим:

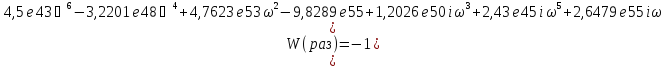
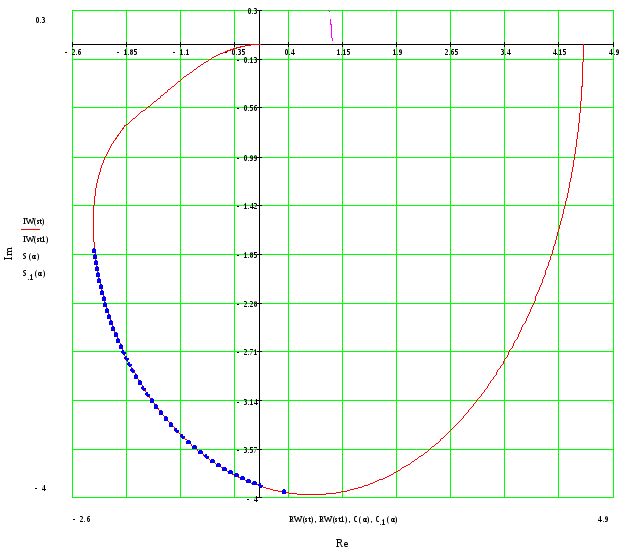
На основании того, что график не охватывает точку (-1;0) мы можем сделать вывод, что система устойчива.

8. Расчёт и построение переходной характеристики нескорректированной сау

Переходная характеристика h(t) - это реакция системы на входное единичное ступенчатое воздействие при нулевых начальных условиях.

Для реальной системы переходную характеристику можно получить экспериментальным путем; при этом на вход системы следует подавать ступенчатое воздействие и фиксировать реакцию на выходе.

Для анализа и синтеза САУ в ТАУ широкое распространение при решении дифференциальных уравнений получил операторный метод. Его основным достоинством является сведение решения системы дифференциальных уравнений к решению системы нормальных алгебраических уравнений.

В ТАУ в качестве математического аппарата для анализа линейных уравнений движения систем выступает операторное преобразование Лапласа.

Преобразова́ние Лапла́са — интегральное преобразование, связывающее функцию F(s) комплексного переменного (изображение) с функцией f(x) действительного переменного (оригинал).

Подадим на вход системы единичное ступенчатое управляющее воздействие и произведём обратное преобразование Лапласа с помощью встроенных средств MathCAD:

h(t)= =

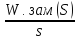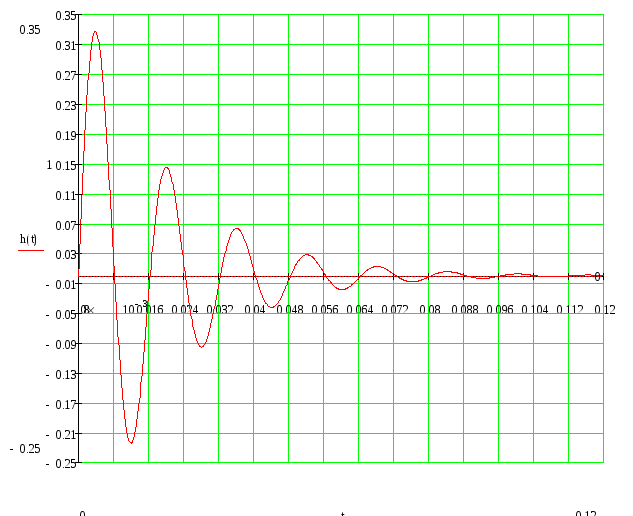
9. Синтез корректирующего звена

Корректирующие звенья – динамические звенья с определенными передаточными функциями. Термин “корректирующие звенья” используется для звеньев, вводимых как для изменения динамических свойств, так и для изменения статических свойств системы. Звенья, использующиеся для повышения запаса устойчивости (динамические свойства), называют иногда демпфирующими, или стабилизирующими. При этом имеется в виду, что эти звенья демпфируют (гасят) колебания, которые возникают в системе регулирования.

Построим на одной плоскости ЛАХ нескорректированной САУ, желаемую ЛАХ и получим ЛАХ регулятора:

По ЛАХ регулятора находим его передаточную функцию:

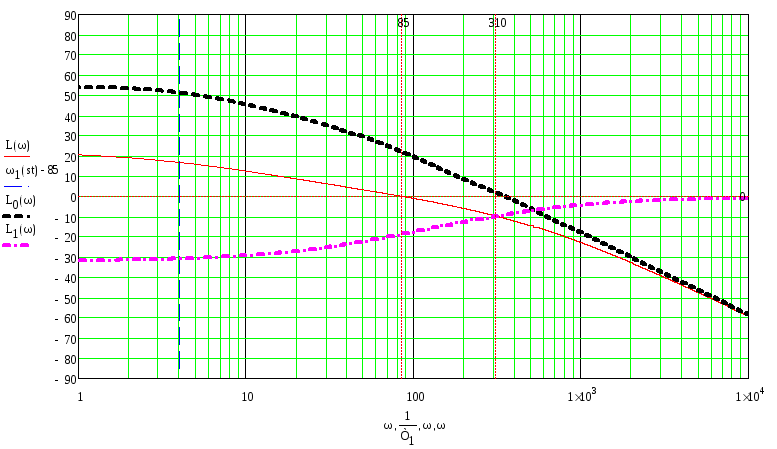
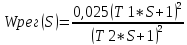
Включаем регулятор последовательно с замкнутой системой.

W(P)=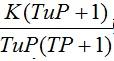-реальное звено. Тр+1 – инерционная часть. Последовательная добавка такого звена в контур системы позволяет повысить точность установившегося режима, т.к.это звено воздействует на низкочастотный участок системы. Включение этого звена позволяет снизить статическую ошибку системы ПИД-звено – фильтр низкой и высокой частоты. Изменяя К, мы приподнимаем второй участок графика или опускаем его. Введение этого звена приводит к повышению точности, расширению полосы пропускания, улучшению динамических свойств. ПИД-звено позволяет корректировать одновременно низкочастотный участок ЛАХ (повышается точность системы) и среднечастотный участок (улучшение динамических свойств). В промышленности выпускаются звенья для решения задач синтеза систем в виде ПИ, ПД и ПИД-регуляторов.