4. Разработка структурной схемы и вывод необходимых передаточных функций

Структурная схема ( Структурная схема САУ, схема САУ )- это изображение системы регулирования в виде совокупности динамических звеньев с указанием связей между ними.

Структурная схема САУ может быть составлена на основе известных уравнений системы, и, наоборот, уравнения системы могут быть получены из структурной схемы.

Для получения структурной схемы заменим в функциональной схеме (рис.2) названия звеньев на их передаточные функции, а также добавим звено-интегратор для сопряжения единиц измерения:

Рис.3

Рис.4

Рис.5

Передаточная функция прямой цепи:

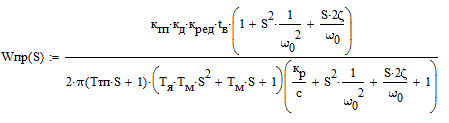(4.0)

Передаточная функция обратной связи:

(4.1)

Передаточная функция разомкнутой системы:

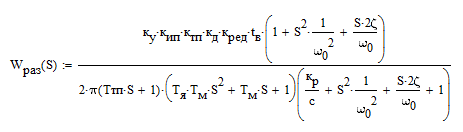(4.2)

Передаточная функция замкнутой системы: (4.3)

5. Анализ устойчивости по критерию Гурвица

Устойчивость — это свойство системы возвращаться в исходный или близкий к нему установившийся режим после всякого выхода из него в результате какого-либо воздействия

Сформулируем критерий Гурвица:

Для того, чтобы динамическая система была устойчива, необходимо и достаточно, чтобы все n диагональных миноров определителя Гурвица были положительны.

Из коэффициентов характеристического уравнения строится определитель Гурвица по алгоритму:

1) по главной диагонали слева направо выставляются все коэффициенты характеристического уравнения от до ;

2) от каждого элемента диагонали вверх и вниз достраиваются столбцы определителя так, чтобы индексы убывали сверху вниз;

3) на место коэффициентов с индексами меньше нуля или больше ставятся нули.

Диагональные миноры- это миноры, включающие в себя n первых диагональных элементов, если размерность минора n*n.

Для проведения расчёта необходимо получить кр. Для его получения воспользуемся разделом 7.3 [1]. Получим:

k_p=2,5Cp*〖V_0〗^x*y*H_0^(y-1)*S_0^z=912,722

Характеристический полином – это знаменатель передаточной функции системы:

D(S)=

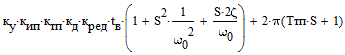
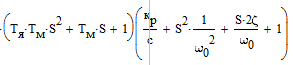
Рассчитаем характеристический полином:

D(S)=3,269e(-7) S^4+0,000139S^3+0,0835S^2+16,8369S+3832,43

Составим матрицу коэффициентов характеристического полинома:

Составим определитель Гурвица:

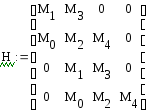
Рассчитаем диагональные миноры:

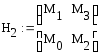
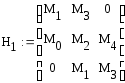
Необходимым (но не достаточным) условием устойчивости является требование, чтобы все коэффициенты ai,i=0,…,n, были одного знака (например, положительные). Если хотя бы один коэффициент полинома имеет противоположный знак относительно других коэффициентов, то это уже является достаточным условием принадлежности одного или нескольких корней правой полуплоскости.

По отсутствию отрицательных определителей делаем вывод, что система устойчива.

6. Анализ устойчивости по критерию Михайлова

Сформулируем критерий Михайлова: система устойчива, если годограф D(jw), начинаясь на действительной положительной полуоси, огибает против часовой стрелки начало координат, проходя последовательно n квадрантов, где n - порядок системы.

Приведём характеристический полином к стандартному виду, для чего разделим его на . И заменимS на :

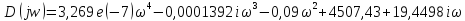
Выделяем мнимую и вещественные части и строим годограф Михайлова: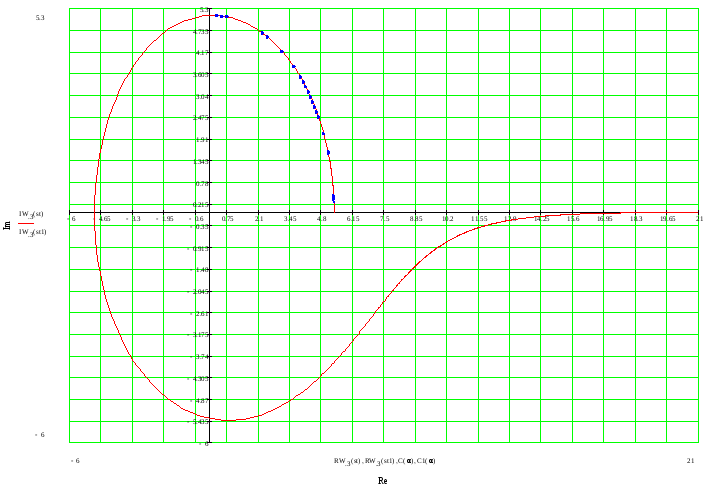

Так как годограф Михайлова проходит последовательно 4 квадранта, огибая начало координат против часовой стрелки, делаем вывод, что система устойчива.