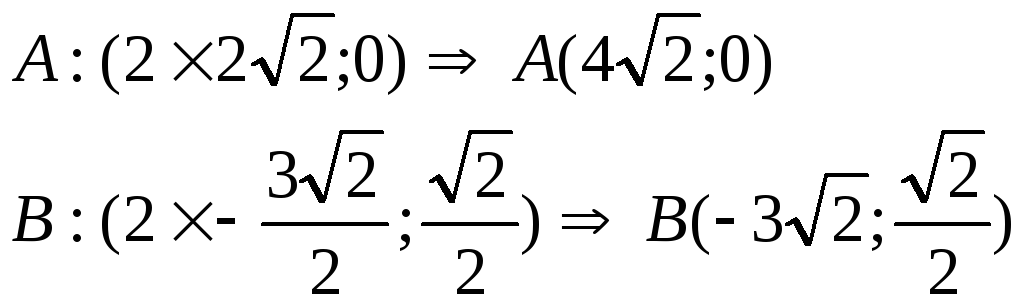3. Табулированная функция.

Как правило, это средство является способом задания сложных кривых.

Схема формирования изображения.

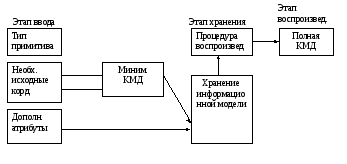
Миним. КМД – минимальная корд. модель- минимальный набор, необходимый для задания изображения ( для линии – х,у, для окружности- 3 точки или центр и радиус).

8.4. Примеры вычислительной геометрии.

Методы ВГ позволяют использовать аналитику для преобразования, хранения и воспроизведения различных геометрических объектов вычислительными методами.

Прямая.

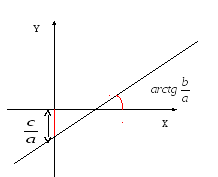
1.Аналитическое уравнение прямой.

,

если а=0, тогда , что непонятно и сложно для ЭВМ. Здесь нет закона, позволяющего построить каждую точку для получения полной КМД.

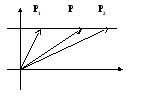
2.Параметрическое уравнение прямой.

Пусть прямая проходит через две точки P₁ и P₂ . Каждая из этих точек в ДСК задаётся с помощью своего радиус- вектора .Прямая представляет из себя множество точек. Произвольная точка P, принадлежащая нашей прямой будет задаваться с помощью радиус-вектора.

Здесь положение векторадля воспроизведения текущей точки определяется неким коэффициентом пропорциональности, который показывает перемещение вектора.Видно, что припопадаем в точкуP₁ (вектор совпадает с вектором), а припопадаем в точкуP₂

Т.о.

Используется линейное приращение, можно воспроизвести все точки прямой.

Определить пересечение двух прямых в 3-D пространстве.

1-я прямая проходит через точки: M₁(1,1,1) ; M₂(2,3,4)

2-я прямая проходит через точки : N₁(1,2,3) ; N₂(-2,-3,-4)

Запишем параметрическое уравнение для каждой прямой:

:

В декартовых координатах прямые:

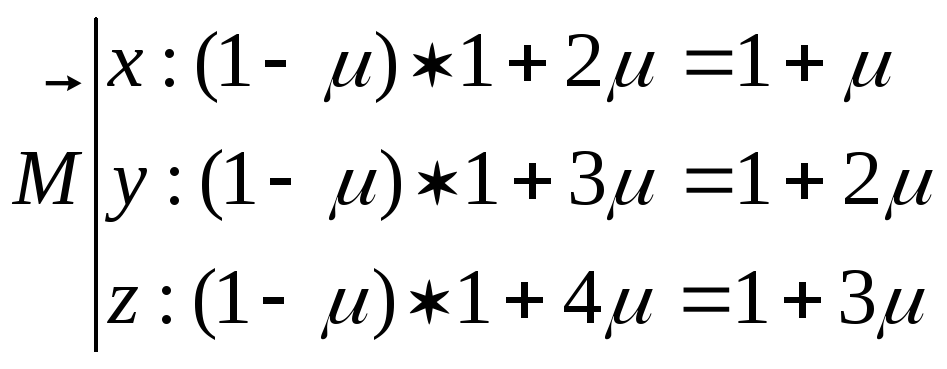
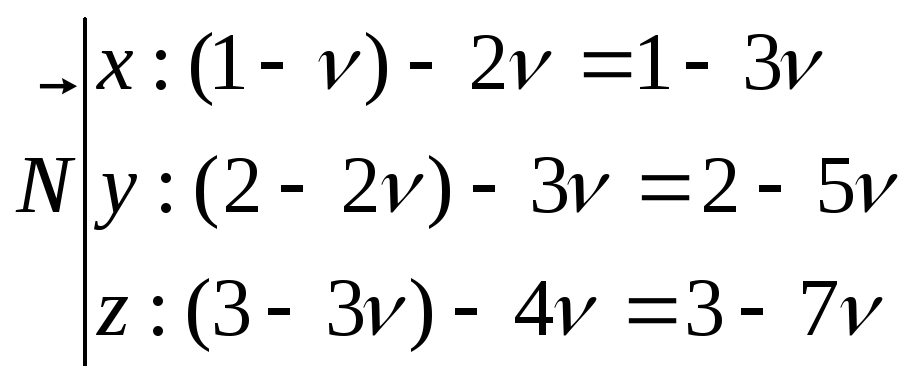
Условие пересечения 2-х прямых предполагает наличие одной общей точки. Приравниваем выражения для соответствующих координат:

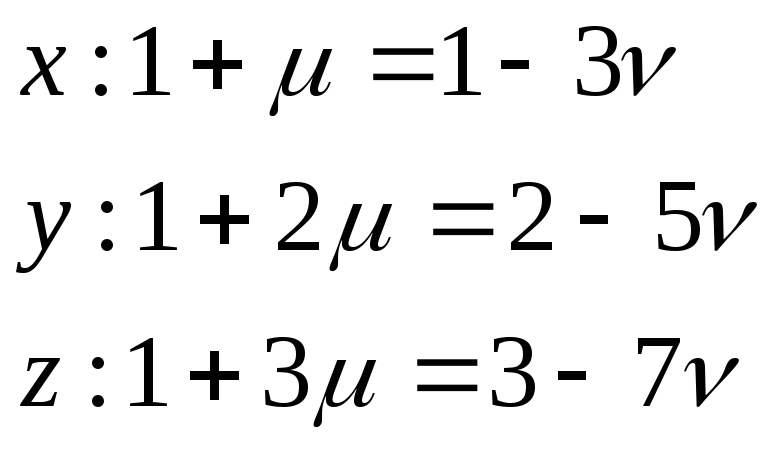
Решение сводится к нахождению 2-х линейно-независимых уравнений, их решению относительно неизвестных и проверке третьего (подстановкой). Выразим из 1-го уравнения Подставим полученное выражение в 3-е уравнение:

, соответственно .

Для проверки подставляем во 2-е уравнение:

1+6=2+5

Полученные параметры подставим в уравнения и при условии равенства координат в обоих уравнениях получим точки пересечения:

-2(1,1,1)+3(2,3,4) = (4,7,10)

2(1,2,3)+(-1)(-2,-3,-4)= (4,7,10)

Прямые пересекаются.

8.5. Преобразования координат в 2d пространстве.

Независимо от выбранного метода проектирования при помощи ЭВМ необходимо иметь в памяти ЭВМ численные данные, описывающие проектируемый объект в некоторой системе (или системах) координат. Если же отдельные части конструкции описываются в различных системах координат, то в памяти машины необходимо иметь данные, описывающие соотношения между выбранными системами координат, с тем чтобы определить относительное положение и ориентацию частей объекта. Эти соотношения, описывающие переход от одной системы координат к другой, называются преобразованиями координат.

В процессе проектирования на любой его стадии может возникнуть необходимость изучения проекта, для чего выполняются чертежи проекции или поперечных сечений проектируемого объекта. Для наглядности чертежи могут быть сделаны в перспективе. Все эти чертежи получаются преобразованием координат объекта в координаты чертежа.

Перед запуском готового проекта в производство система координат, в которой данный проект был выполнен, должна быть соотнесена с системой координат станка; т.о., и на этой стадии необходимо преобразование координат.

Если же проект обладает той или иной симметрией, то в памяти машины достаточно иметь данные, описывающие лишь часть проекта, поскольку чертеж полной конструкции на основании симметрии можно получить при помощи вращений, сдвигов и отражений. Выполняемые в данном случае преобразования являются преобразованиями объектов и совершенно не влияют на систему координат, в которой данный предмет был изображен.

В основе преобразования координат лежат 3 основные формы изменения координатной модели (переход от заданной системы координат к системе координат наблюдателя):

1. перенос;

2. изменение масштаба;

3. поворот осей координат.

Как правило, принято, что само пространство не изменяется, и положение объекта мы считаем неизменным, меняется координатная система наблюдателя.

1. Перенос.

Если идет речь о переносе объекта, то связь между радиус-вектором r^/ перемещенной точки и ее первоначальным положением устанавливается соотношением: где t - вектор перемещения каждой точки рассматриваемого объекта.

Если же переносятся оси координат, а объект фиксирован, тогда связь между координатами новой системы координат O^/x^/y^/ и координатами старой системы Oxy задается соотношениями: , где (t,к) координаты начала новой с.к. относительно старой с.к.

Если новое начало соответствует некоторой точке в старой с.к с координатами О^/(t;k). Тогда некоторая точка К(х;у) из прежней системы координат в новой будет выглядеть как К(х-t,y-k).

Например, если начало новой с.к. лежит в т.О^/(4,6), а т.К в старой с.к. имеет координаты (3,3), тогда в новой с.к. т.К(3-4,3-6), т.е. К(-1,-3).

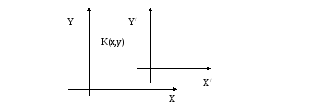
2)Изменение масштаба.

Новая и старая с.к. имеют одно начало координат, но различные масштабы по осям. Отрезок в одну единицу по оси абсцисс будет соответствовать в новой системе S_x, по оси Y будет соответствовать S_y. Тем самым меняется масштаб точки, т.е ее удаленность от начала координат.

3)Поворот осей координат.

O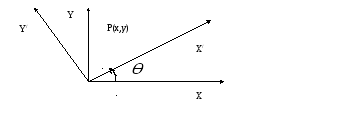

Пусть новая и старая с.к. имеют общее начало и масштаб. Новая с.к повернута относительно старой против часовой стрелки на угол . Пусть в старой с.к задана т.Р(х;у). Выразим ее координаты в новой с.к через известные координаты:

Полное преобразование координат производится строго в определенной последовательности:

2. Перенос в начало координат;

3. Поворот осей;

4. Изменение масштаба.

Пример.

Пусть на плоскости задан отрезок прямой АВ: А(3,2) и В(-1,-1). Что произойдет с отрезком при полной смене координат наблюдателя, если: 1) начало координат переносится в точку (1,0);

2) произойдет поворот осей на угол

3) изменение масштаба по оси Х вдвое.

Решение:

1. в новой с.к. отрезок будет иметь следующие координаты: А(3-1, 2-0) и В(-1-1, -1-0), т.е А(2,2) и В(-2, -1);

2. при повороте осей в новой с.к:

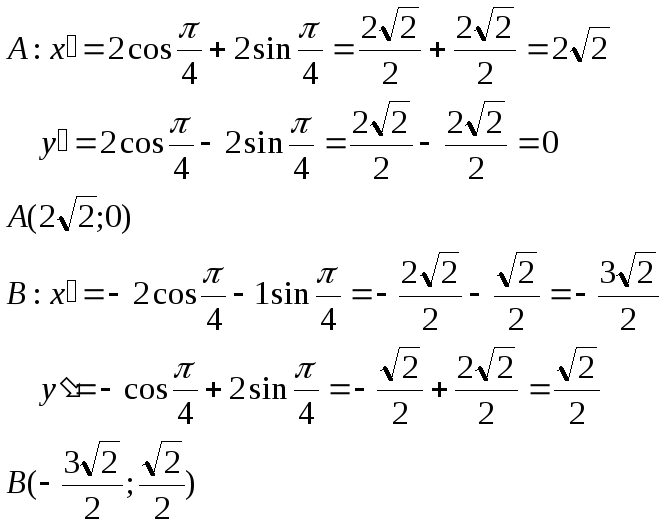
3. изменение масштаба, S_x=2