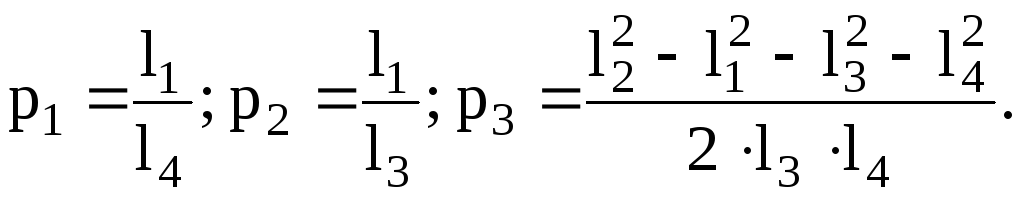- •Конспект лекций
- •2008 Г.
- •Часть 1. Структурный анализ и синтез механизмов 6
- •Часть 2. Кинематический анализ механизмов 57
- •Часть 3. Динамический анализ механизмов 99
- •Часть 4. Анализ движения механизма под действием сил 132
- •Введение
- •Часть 1. Структурный анализ и синтез механизмов
- •1. Введение в теорию механизмов и машин. Предмет и задачи курса тмм
- •2. Структура механизмов
- •2.1. Основные понятия теории механизмов и машин
- •2.2. Классификация кинематических пар
- •2.3. Кинематические цепи и кинематическая схема механизма
- •2.4. Степень подвижности механизма
- •2.5. Структурный анализ плоских механизмов
- •2.6. Замена в плоских механизмах высших пар низшими
- •2.7. Классификация механизмов (виды механизмов)
- •1. Рычажные механизмы
- •2. Кулачковые механизмы
- •3. Зубчатые механизмы
- •2.9. Синтез зубчатых механизмов
- •3. Манипуляторы и промышленные роботы
- •3.1. Виды манипуляторов и промышленных роботов
- •3.2. Структура и геометрия манипуляторов
- •3.3. Рабочий объем манипуляторов и классификация движения захвата
- •3.4. Структурный синтез манипуляторов
- •3.5. Зоны обслуживания, угол и коэффициент сервиса
- •Часть 2. Кинематический анализ механизмов
- •1. Кулачковые механизмы
- •1.1. Кинематический анализ кулачковых механизмов методом диаграмм
- •1.2. Угол передачи движения, его определение
- •1.3. Синтез кулачковых механизмов
- •2. Кинематика зубчатых передач
- •2.1. Передаточное отношение последовательного ряда колёс
- •2.2. Передаточное отношение ступенчатого ряда колёс
- •2.3. Передаточное отношение планетарных и дифференциальных механизмов
- •2.4. Графический метод кинематического исследования зубчатых механизмов.
- •2.5. Синтез планетарных механизмов
- •3. Кинематический анализ рычажных механизмов
- •3.1. Построение положений механизма и траекторий его точек
- •3.2. Определения аналогов величин скоростей и ускорений
- •3.7. Построение полярных планов аналогов скоростей
- •3.8. Построение планов аналогов скоростей методом эпюр
- •3.9. Определение аналогов ускорений в механизме
- •3.10. Определение скоростей и ускорений методом построения кинематических диаграмм
- •3.11. Кинематическое исследование рычажных механизмов аналитическим методом
- •Часть 3. Динамический анализ механизмов
- •1. Задачи кинетостатики
- •2. Силы, действующие на механизм
- •2.1. Классификация сил
- •2.2. Внешние силы и механические характеристики машин
- •2.3. Определение сил инерции
- •3. Силовой анализ механизмов. Определение реакций в кинематических парах
- •4. Трение в кинематических парах
- •4.1. Трение скольжения
- •4.2. Сухое трение
- •4.3. Жидкостное трение
- •4.4. Трение при скольжении ползуна по горизонтальной плоскости
- •4.5. Трение в кинематической паре шип – подшипник
- •5. Коэффициент полезного действия механизма
- •6. Определение реакций в кинематических парах с учетом трения
- •6.1. Силовой анализ зубчатых механизмов
- •6.2. Определение моментов в планетарном механизме без учета трения
- •6.3. Определение коэффициента полезного действия планетарного механизма
- •6.4. Силовой расчет кулачковых механизмов.
- •Часть 4. Анализ движения механизма под действием сил
- •1. Уравновешивание механизмов
- •1.1. Общие сведения
- •1.2. Уравновешивание вращающихся тел
- •1.3. Уравновешивание механизмов на фундаменте
- •2. Анализ движения механизма под действием сил
- •2.1. Основные режимы движения механизма
- •2.2. Приведение масс, сил и моментов
- •2.3. Уравнение движения механизма
- •2.4. Определение момента инерции махового колеса
- •2.5. Методика определения момента инерции махового колеса
- •Литература
2. Кулачковые механизмы
Кулачковые механизмы служат для сообщения ведомому звену периодического движения по заданному закону, обусловленному профилем кулачка.
На (рис. 1.17) показан кулачковый механизм , где:
1 – кулачок вращающийся вокруг точки А
2 – поступательно движущийся толкатель
Кулачковые механизмы применяются в машинах автоматах, прядильных машина, ДВС, и т.д.

Рис. 1.17
Основные виды кулачковых механизмов
Кулачком называется звено, которому принадлежит элемент высшей кинематической пары, выполненный в виде поверхности переменной кривизны. Механизм, в состав которого входит кулачок, называется кулачковым механизмом.
В рассмотренных ранее зубчатых механизмах каждый зуб может рассматриваться как кулачок. Выходное звено кулачковых механизмов, как правило, совершает возвратное движение.
Прямолинейно движущееся выходное звено кулачкового механизма называется толкателем, а качающееся – коромыслом.
|
|
|
а) |
|
|
|
|
|
б) |
в) |
г) |
|
Рис. 1.18 | ||
Для уменьшения трения о поверхность кулачка выходное звено часто снабжают роликом.
Постоянное соприкосновение звеньев в высшей паре обеспечивается или силовым, или геометрическим замыканием.
При силовом замыкании постоянное прижатие звеньев происходит под действием пружины, силы тяжести и т.д. (рис. 1.18а)
При геометрическом замыкании возможность отрыва одного звена от другого устраняется введением дополнительной (избыточной) геометрической связи.
Одним из наиболее распространенных способов геометрического замыкания является применение пазового кулачка (рис. 1.18б).
Трудность точного выполнения паза и устранения ударов ролика привели к появлению двухдисковых кулачков (рис. 1.18в).
Вместо двухдисковых кулачков выполняют диаметральный кулачок
(рис. 1.18г).
3. Зубчатые механизмы
Зубчатые механизмы применяются для передачи вращательного движения между валами посредством зубчатого зацепления.

Рис. 1.19
Зубчатые механизмы наиболее широко применяются в технике и имеют большое количество видов.
4. Клиновые механизмы
К клиновым механизмам относятся механизмы, в которых звенья обладают только поступательным движением.
Поступательное
движение звена 1 в направлении х-х
вызывается поступательным движением
звена 2 в направлении у-у, при этом
увеличивается усилие на выходном звене
(![]() )
)

Рис. 1.20
5. Винтовые механизмы

Рис. 1.21
К винтовым механизмам относятся механизмы, звенья которых имеют винтовые движения (связывают между собой вращательное и поступательное движения).
6. Фрикционные механизмы
Во фрикционных механизмах передача движения от ведущего звена к ведомого осуществляется по средствам сил трения. Эти механизмы используются в муфтах, в вариаторах.

Рис. 1.22
7. Гидравлические механизмы
1. – гидроцилиндр
2. – управляющий клапан
3. – поршень
В гидравлических механизмах для осуществления поступательного или вращательного движения исполнительного звена используется энергия находящаяся под давлением жидкости.

Рис. 1.23
8. Пневматические механизмы
Пневматические механизмы – осуществляют движение исполнительного звена за счет энергии сжатого воздуха.
9. Механизмы с электрическим устройством
Механизмы с электрическим устройством используются в качестве элементов, работающих на принципе воздействия электрических полей (электрические реле).
2.8. Синтез шарнирного четырехзвенника
Пусть
заданы (рис. 1.24) длина стойки
![]() ,
угловые координаты входного звена 1 в
трех положениях:
,
угловые координаты входного звена 1 в
трех положениях:![]() и соответствующие угловые координаты
выходного звена 3:
и соответствующие угловые координаты
выходного звена 3:![]() .
Нужно найти длины звеньев
.
Нужно найти длины звеньев![]() .
.
Рассмотрим
векторный контур АВСДА, для которого в
любом положении механизма
![]() .
Проецируя этот контур на координатные
оси X и У, имеем:
.
Проецируя этот контур на координатные
оси X и У, имеем:
|
|
|
(1.4.) (1.5.) |
Исключим
угол
![]() ,
решив уравнения (1.4) и (1.5) относительно
слагаемых, содержащих
,
решив уравнения (1.4) и (1.5) относительно
слагаемых, содержащих![]() ,
возведя полученные равенства в квадрат
и сложив их:
,
возведя полученные равенства в квадрат
и сложив их:
![]()
После
деления на
![]() и
замены текущих значений углов
и
замены текущих значений углов![]() и
и![]() на заданные
на заданные![]() и
и![]() (индекс i=1, 2, 3), получим систему трех
линейных уравнений:
(индекс i=1, 2, 3), получим систему трех
линейных уравнений:
![]()
или
|
|
|
(1.6) |
где неизвестными являются безразмерные параметры:
|
|
|
(1.7) |
Из
системы (1.6) находим,
![]() а затем согласно (1.7) находим искомые
длины звеньев по формулам:
а затем согласно (1.7) находим искомые
длины звеньев по формулам:

Задачу
синтеза шарнирного четырёхзвенника по
трем положениям выходного звена и
соответствующим углам поворота входного
звена решают методом обращения движения.
В этом случае заданы длины звеньев
![]() координаты выходного звена 3 в трех
положениях
координаты выходного звена 3 в трех
положениях![]() и углы поворота входного звена
и углы поворота входного звена![]() и
и![]() .
Требуется найти длины звеньев
.
Требуется найти длины звеньев![]() и
начальную угловую координату (в положение
1)
и
начальную угловую координату (в положение
1)![]() .
.
Положение
шарнира В по заданным условиям находят
путем сообщения всему механизму
относительно центра А угловой скорости
![]() .
В результате звено АВ в системе координат
.
В результате звено АВ в системе координат![]() станет неподвижной, а вместо него в
противоположном направлении будет
вращаться стойка
станет неподвижной, а вместо него в
противоположном направлении будет
вращаться стойка![]() (рис. 1.25). Для второго и третьего положения
механизма угловыми координатами стойки
по отношению к оси абсцисс будут -
(рис. 1.25). Для второго и третьего положения
механизма угловыми координатами стойки
по отношению к оси абсцисс будут -![]() и -
и -![]() .
Положение шарнира С является определенным
по отношению к стойке и найдется путем
построения заданных углов
.
Положение шарнира С является определенным
по отношению к стойке и найдется путем
построения заданных углов![]() (точки
(точки![]() ,
,![]() ,
,![]() ).
Длина шатуна ВС для трех заданных
положений одна и та же
).
Длина шатуна ВС для трех заданных
положений одна и та же![]() ,
поэтому точки
,
поэтому точки![]() должны находиться на окружности,
описанной из центра В. Следовательно,
положение неизвестной точки В найдется,
если точки
должны находиться на окружности,
описанной из центра В. Следовательно,
положение неизвестной точки В найдется,
если точки![]() соединить двумя прямыми
соединить двумя прямыми![]()
![]() и
и![]()
![]() ,
провести через их середины
,
провести через их середины![]() ,
,![]() перпендикуляры и найти точку пересечения
последних. При аналитическом решении
для получения формул координат
перпендикуляры и найти точку пересечения
последних. При аналитическом решении
для получения формул координат![]() точек
точек![]() кинематическая цепь
кинематическая цепь![]() представленного в виде суммы двух
векторов
представленного в виде суммы двух
векторов![]() и
и![]() .
Координаты точек
.
Координаты точек![]() определяются проекциями указанной
векторной цепи на координатные оси:
определяются проекциями указанной
векторной цепи на координатные оси:
![]()
![]()
Координаты
точки В найдем из системы уравнений
окружности, описанной из центра В
радиусом
![]() :
:
|
|
|
(1.8) |
Система
(1.8) трех уравнений с тремя неизвестными
![]() и
и![]() после несложных преобразований для
исключения
после несложных преобразований для
исключения![]() и
и![]() сводится к линейной.
сводится к линейной.
По
координатам
![]() и
и![]() определяют искомые параметры кинематической
схемы механизма:
определяют искомые параметры кинематической
схемы механизма:
длину входного звена 1:
![]()
длину шатуна ВС:
|
|
|
|
Рис. 1.24 |
|
|
| |
|
Рис. 1.25 | |
![]()
(как
расстояние между точками
![]() и
и
![]() );
);
начальную угловую координату входного звена:
![]()