Нахождение резонансной емкости

В общем случае резонанс напряжений в цепи, содержащей реактивные элементы, наступает при равной нулю мнимой составляющей комплексного сопротивления Z_Im=0. Рассмотрим это на примере простой цепи, содержащей последовательно соединённые резистор, катушку и конденсатор.

R	C	L

Найдём комплексное сопротивление ветви:

Таким образом, в рассматриваемой цепи мнимая составляющая комплексного сопротивления равна нулю при равенстве сопротивлений конденсатора и катушки:

Или, если выразить реактивные сопротивления через параметры LиC:

Нетрудно увидеть, что при резонансе в рассматриваемой цепи сопротивление минимально. В соответствии с законом Ома: , ток при резонансе максимален.

Для экспериментального определения величины ёмкости, при которой в цепи наступит резонанс, пользуются зависимостью тока от ёмкости.

В заданной цепи изменяют ёмкость в определённых пределах, и снимают значение величины тока в ветви с конденсатором. Точка, в которой ток максимален показывает резонансную ёмкость.

§2.9. Примеры и задачи

2.9.1. Синусоидальные величины и их символическое изображение

Мгновенные значения синусоидальной величины определяются выражением:

,

где – амплитуда;

– действующее значение;

– угловая частота, [с^-1];

– линейная частота, [Гц];

– период колебаний [c];

 – начальная фаза, [рад].

Расчет цепей переменного тока облегчается, если изображать гармонические токи, напряжения и ЭДС векторами на комплексной плоскости.

Совокупность векторов, изображающих синусоидальные функции в заданный момент времени, называется векторной диаграммой.

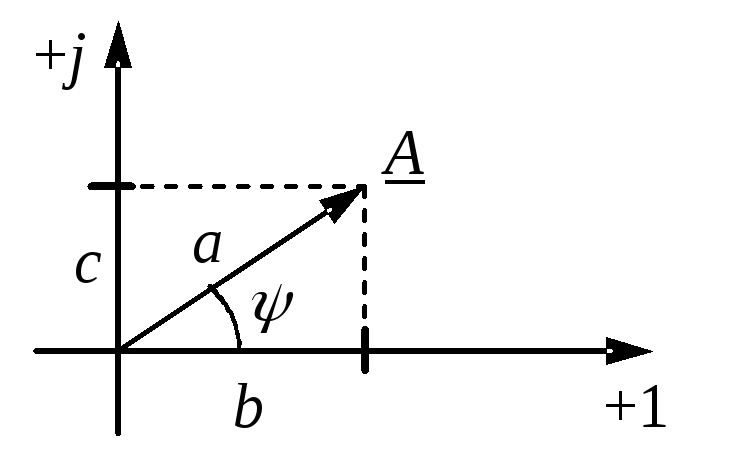
Комплексное число может быть представлено в алгебраической и показательной форме:

.

Переход из показательной формы в алгебраическую форму осуществляется по формуле Эйлера:

.

При обратном переходе: , если вещественная часть алгебраической формы положительная, тоа если вещественная часть отрицательная, то

.

Комплексная синусоидальная функция представляется в виде вращающегося вектора на комплексной плоскости:

;

,

,

(при t = 0).

Мгновенное значение синусоидальной функции есть проекция вращающегося вектора на мнимую ось:

.

Обозначения:

i, u, e – мгновенные значения тока, напряжения, ЭДС.

I_m,U_m,E_m– комплексные амплитудные значения тока, напряжения, ЭДС.

I,U,E– комплексные действующие значения тока, напряжения, ЭДС.

Примеры

1.1. Дано синусоидальное напряжение .

Записать выражения для комплексного амплитудного и действующего значения.

Решение:

;

.

1.2. Комплексное действующее значение тока .

Записать выражение для мгновенных значений тока.

Решение:

;

.

2.10.2. Расчет линейных цепей с гармоническими источниками электрической энергии

2.10.2.1. Закон Ома в комплексной форме

Таблица 2.1.

Элемент	Связь между мгновенными значениями напряжения и тока	Связь между комплексными действующими значениями напряжения и тока	Векторная диаграмма	Применение
				Напряжение совпадает по фазе с током.
				Напряжение опережает ток на .
				Напряжение отстает от тока на .

2.10.2.2. Комплексное сопротивление двухполюсника

– активное сопротивление резистораR, [Ом];

– реактивное сопротивление катушки, [Ом];

– индуктивность катушки, [Гн];

– угловая частота, [с ^-1];

– реактивное сопротивление конденсатора, [Ом];

– емкость конденсатора, [Ф];

– комплексное сопротивление резистора;

– комплексное сопротивление катушки;

– комплексное сопротивление конденсатора.

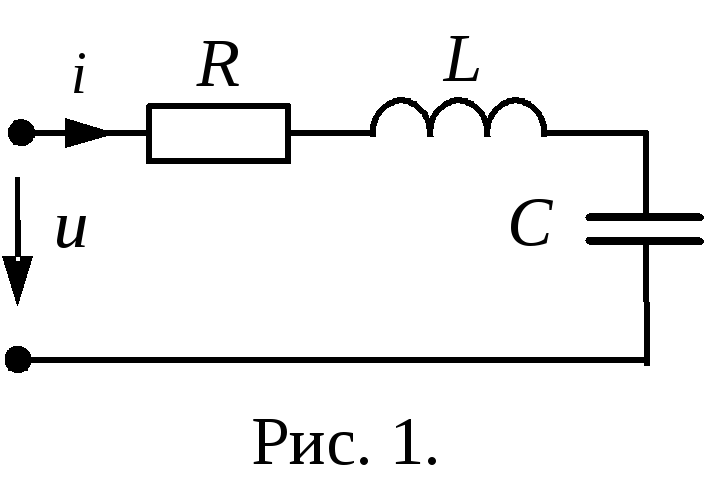
Для цепи (рис. 1) комплексное сопротивление:

где – модуль комплексного сопротивления или полное сопротивление;

– угол сдвига фаз между напряжением и током.