1.8.7. Потенциальная диаграмма
Потенциальная диаграмма – это график распределения потенциалов вдоль какого-либо участка цепи или замкнутого контура. По оси абсцисс на нем откладывают сопротивления вдоль контура, начиная с точки, потенциал которой принимают равным нулю, по оси ординат - потенциалы. Каждой точке рассматриваемого контура соответствует своя точка на потенциальной диаграмме.
ПРИМЕР 1.7.1.
Дано:
Ом;
Ом;
Ом;
Ом;
В;
В;
А;
А;
А.
Построить потенциальную диаграмму для контура авсdа.
Решение:
Подсчитаем суммарное сопротивление
контура авсdа
Ом
и выберем масштабы по оси ординат. Точкуапомещаем в начало координат.
Определяем потенциалыв,с,dи их координаты.
Принимаем
.
Токораспределение в схеме при заземлении
одной точки не изменится, т.к. никаких
новых ветвей при этом не образуется.
В,
;
В,
;
В,
;
В,
.
1.8.8. Метод узловых потенциалов
Метод расчета электрических цепей, в котором за неизвестные принимают потенциалы узлов схемы, называют методом узловых потенциалов. Число неизвестных в этом методе равно числу узлов минус один.
Потенциал одного узла схемы принимают равным нулю, для остальных составляют систему уравнений вида
,
где
- сумма проводимостей ветвей, сходящихся
в узлек;
- сумма проводимостей ветвей, соединяющих
узлыкиm, взятая
со знаком «-»;
- узловой ток узлак. Находится как
алгебраическая сумма токов короткого
замыкания всех ветвей, сходящихся в
узлек. С плюсом берутся те токи,
источники которых направлены к узлук.
Если между двумя узлами нет ветви, то соответствующая проводимость равна нулю.
После решения системы относительно потенциалов определяют токи в ветвях по закону Ома.
ПРИМЕР 1.8.1.
Дано:
Ом;
Ом;
Ом;
Ом;
В;
В;
В;
А.
Определить токи методом узловых потенциалов
.
Решение:
Примем
потенциал узла 4 равным нулю:
,
тогда потенциал
В.
Составим
уравнения для узлов 1 и 2 (при этом учтем,
что проводимость ветви, соединяющей
узлы 1 и 2,
):
Подставляем числовые значения:
В;
В
Токи в ветвях находим по закону Ома:
А;
А;
А;
А.
Ток
находим по первому закону Кирхгофа,
примененному к узлам 3 или 4:
А
или
А.
ЗАДАЧИ
1.8.1. а) Составить уравнения для расчета цепи методом узловых потенциалов.
б)
Определить токи в ветвях методом узловых
потенциалов, если
Ом;
Ом;
Ом;
Ом;
Ом;
Ом;
Ом;
В;
В;
В;
В.
Дано:
Ом;
Ом;
В;
В;
А.
Определить токи методом узловых потенциалов. Построить потенциальную диаграмму для контура 1‑2‑3‑4‑1.
1.8.2. а) Составить уравнения для расчета цепи методом узловых потенциалов.
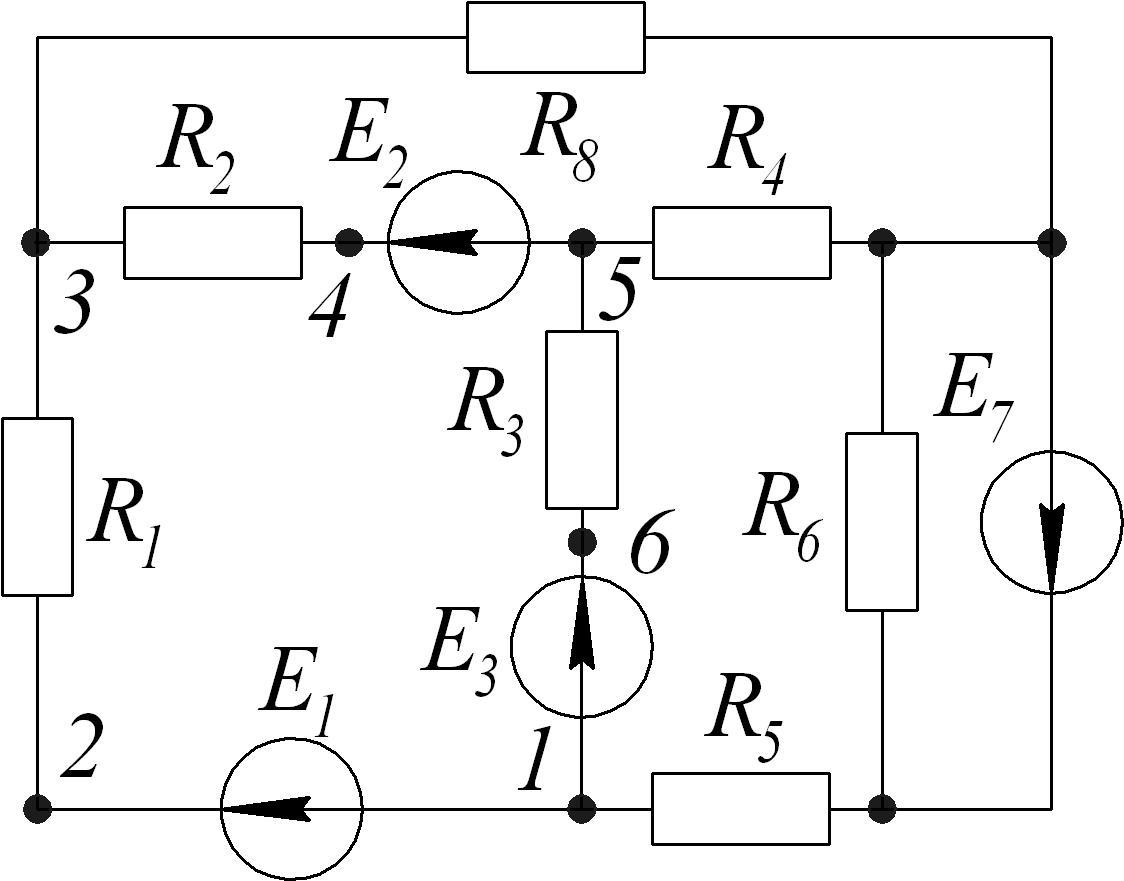
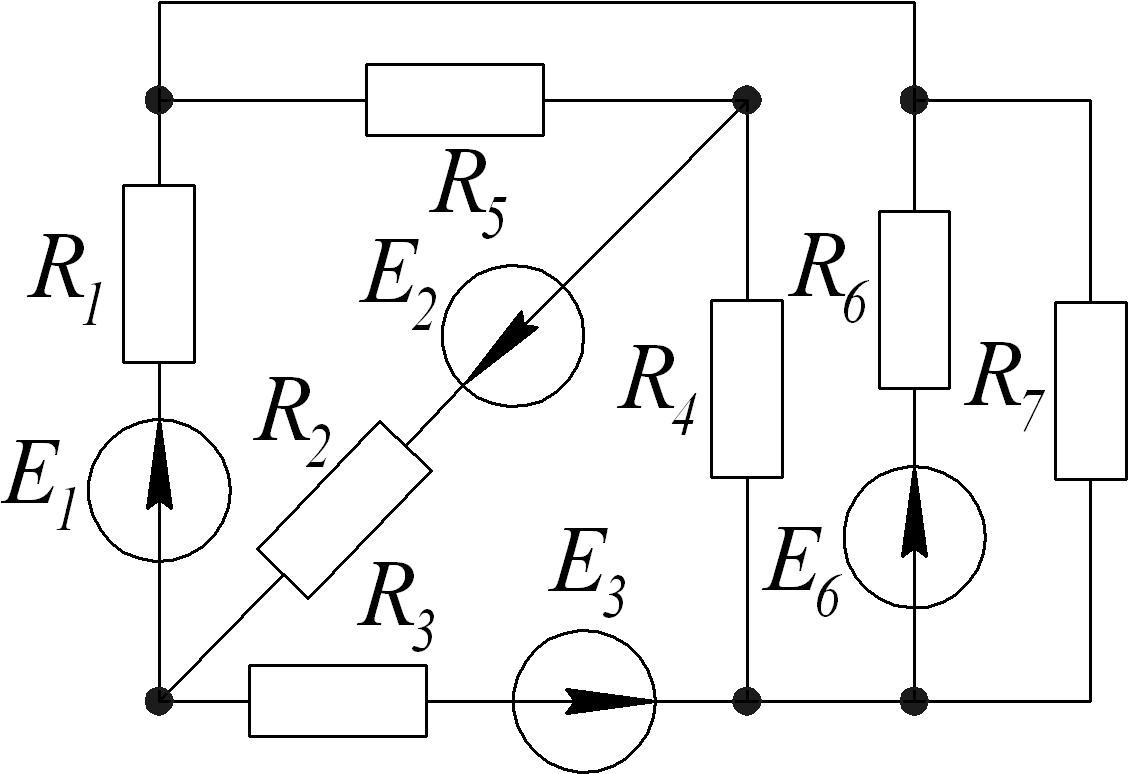
б)
Определить токи в ветвях методом узловых
потенциалов, если
Ом;
Ом;
Ом;
Ом;
Ом;
Ом;
Ом;
В;
В;
В;
В.
Построить потенциальную диаграмму для
контура 1-2-3-4-5-6.
Дано:
Ом;
В;
В;
А.
Определить токи в ветвях методом узловых потенциалов.
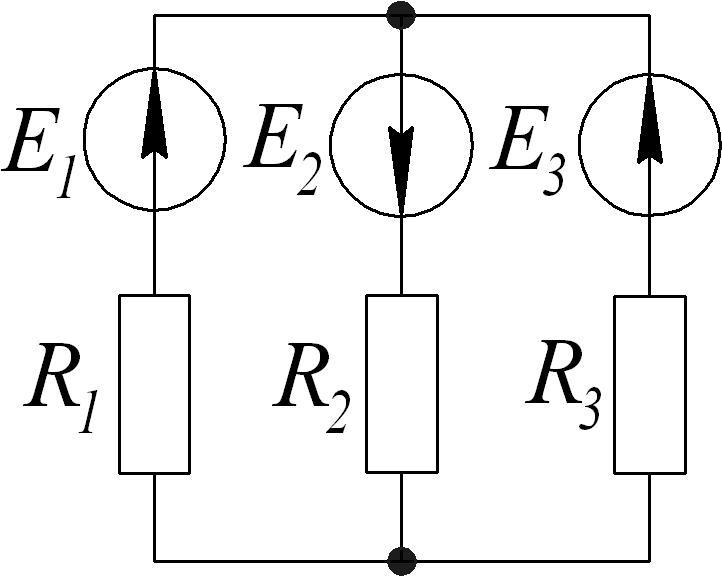
1.8.3. а) Составить уравнения для расчета цепи методом узловых потенциалов.
б)
Определить токи в ветвях методом узловых
потенциалов, если
A;
A;
A;
Ом;
Ом;
Ом;
См;
См;
См;
В.
Дано:
Ом;
Ом;
Ом;
В;
В;
В.
Определить токи в ветвях методом узловых потенциалов.
1.8.4. а) Составить уравнения для расчета цепи методом узловых потенциалов.
б)
Определить токи в ветвях методом узловых
потенциалов, если
Ом;
Ом;
Ом;
Ом;
Ом;
Ом;
Ом;
В;
В;
В;
В;
А
Дано:
Ом;
Ом;
В;
В;
В.
Определить токи методом узловых потенциалов. Построить потенциальную диаграмму для контура 1-2-3-4-1.
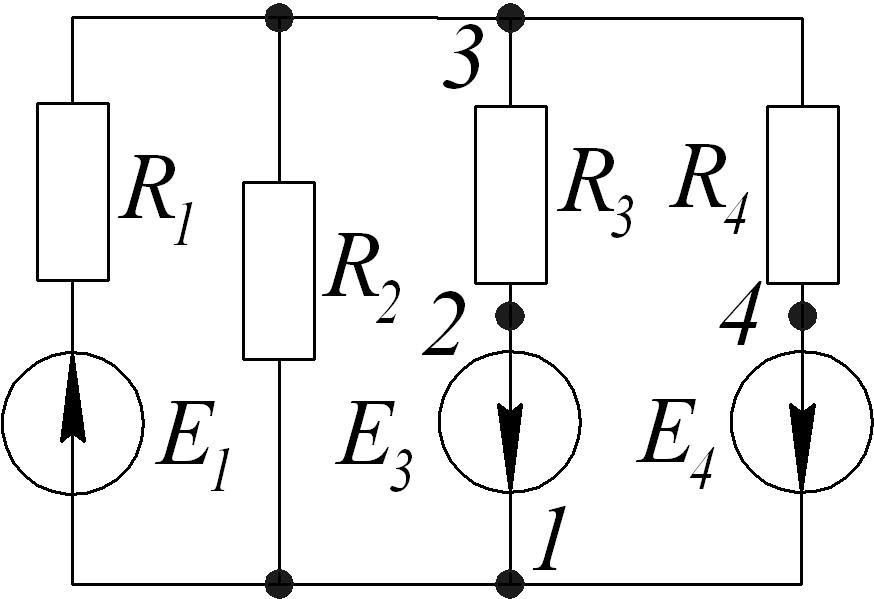
1.8.5.
Определить токи в ветвях методом узловых
потенциалов, если
См;
См;
См;
См;
См;
В;
В;
В.
Дано:
Ом;
Ом;
В;
В;
A.
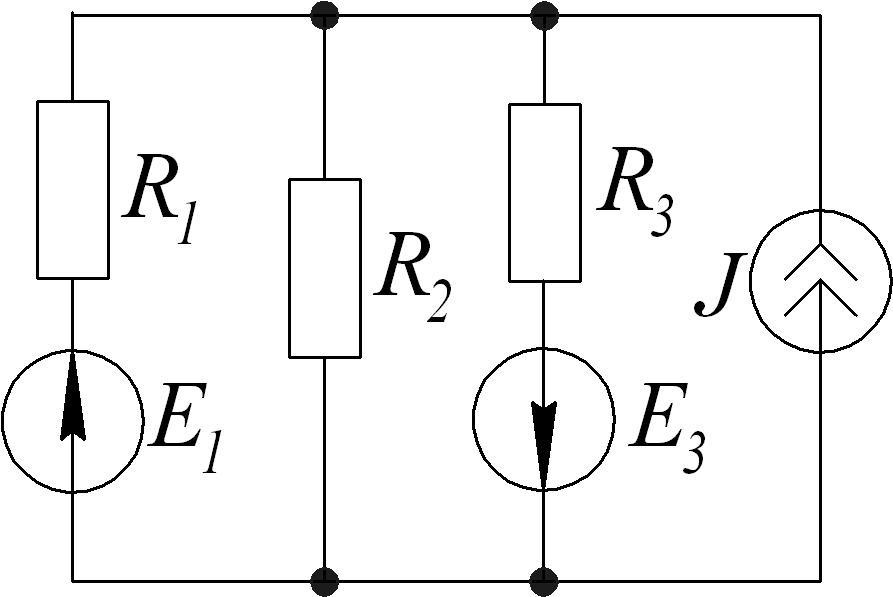
Определить токи в ветвях методом узловых потенциалов.
1.8.6. а) Составить уравнения для расчета цепи методом узловых потенциалов.
б)
Рассчитать токи в ветвях, если
Ом;
Ом;
Ом;
Ом;
Ом;
В;
В;
В;
А.
Дано:
Ом;
Ом;
Ом;
А;
В;
В.
Методом
узловых потенциалов найти токи
и
.
1.8.7. а) Составить уравнения для расчета цепи методом узловых потенциалов.
б)
Рассчитать токи в ветвях методом узловых
потенциалов, если
Ом;
Ом;
Ом;
Ом;
Ом;
Ом;
Ом;
В;
В;
В.
Дано:
Ом;
Ом;
В;
В;
A.
Определить токи в ветвях цепи методом узловых потенциалов.