- •Материалы для студента
- •§ 3.2. Теоретические вопросы Модуля 3
- •§ 3.3. Задание Модуля 3
- •§3.4. Схемы к Модулю 3
- •§3.5. Методические указания к выполнению задания Модуля 3
- •§3.6. Методические указания к выполнению экспериментального исследования Модуля 3
- •§3.6.1. Правила подготовки к экспериментальному лабораторному исследованию
- •§3.6.2. Правила выполнения экспериментального исследования
- •§3.7. Лабораторное исследование к заданию Модуля 3
- •§3.7.1. Подготовка к экспериментальному исследованию
- •§3.7.2. Содержание лабораторного исследования
- •§3.7.3. Описание лабораторной установки
- •§3.7.4. Выполнение лабораторного исследования
- •§3.8. Методические указания к компьютерному моделированию задания модуля 3
- •§3.8.1. Подготовка к компьютерному моделированию
- •§3.8.2. Содержание компьютерного моделирования
- •§3.8.3. Выполнение компьютерного моделирования
- •§3.9. Примеры и задачи
- •§3.9.1. Соединение в звезду
- •§3.9.2. Соединение в треугольник
- •§3.9.3. Активная, реактивная и полная мощность трехфазной системы
- •§ 3.9.4. Трехфазные цепи с несколькими приемниками в симметричном режиме
- •§ 3.9.5. Расчет сложной несимметричной цепи
- •§ 3.10. Вопросы для самопроверки
- •§ 3.11. Примеры тестов по материалу модуля 3
- •3.12. Вопросы для самопроверки
- •Литература
- •3.7. Примеры тестов по материалу модуля 3
- •Литература
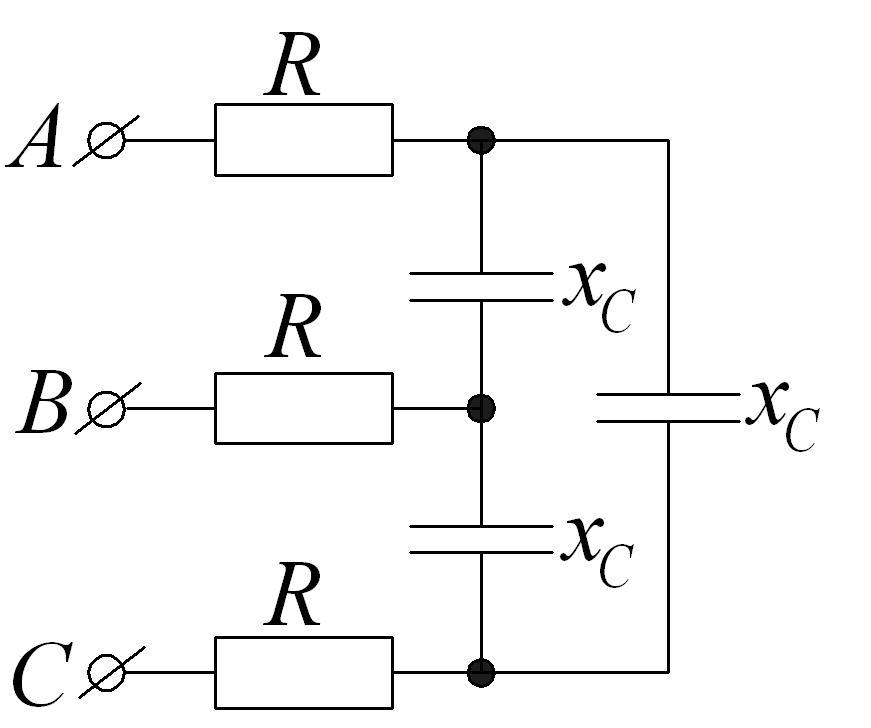
§3.9.2. Соединение в треугольник
Соединение источника и приемника треугольником изображено на рис. 12.
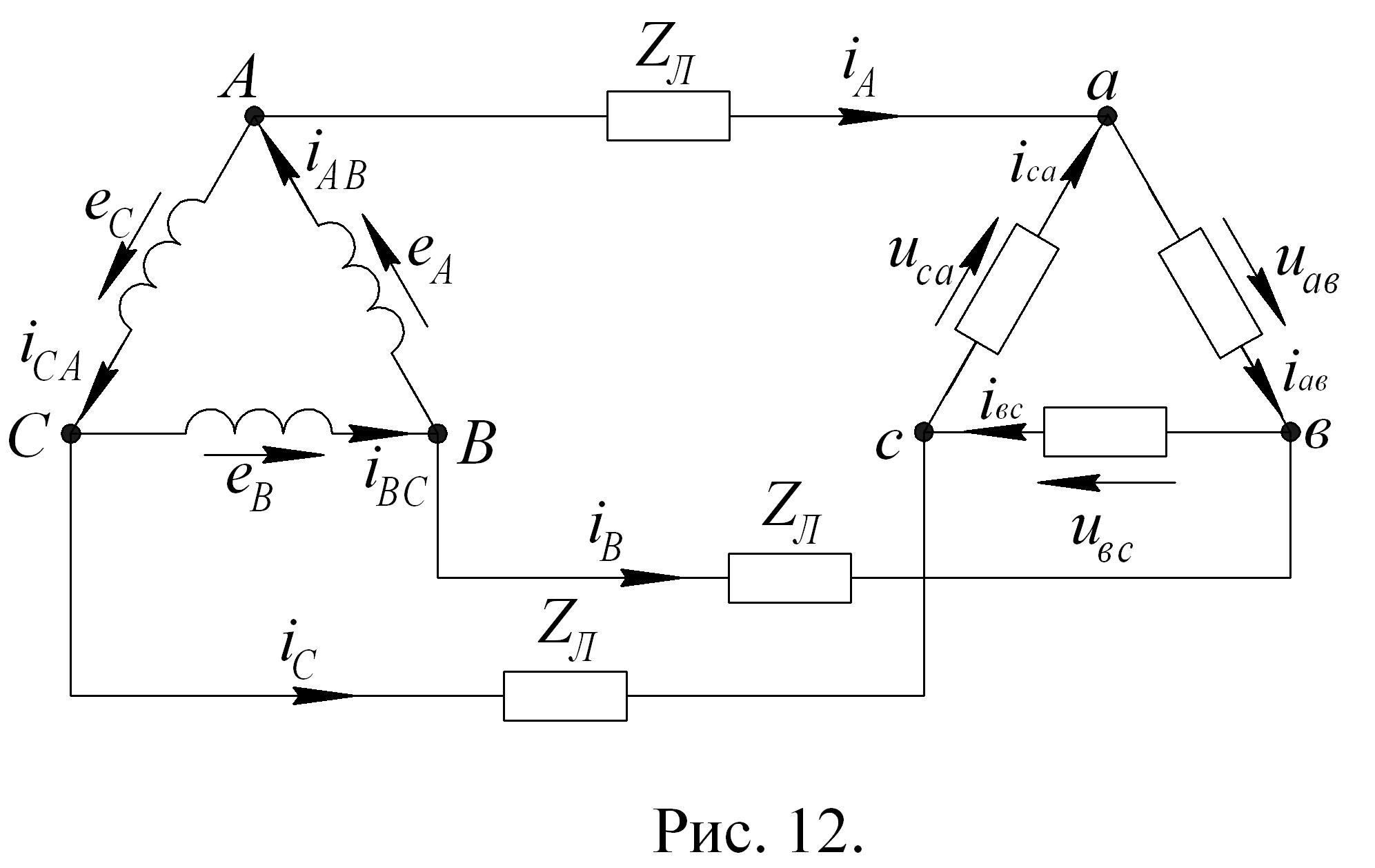
Положительным
направлением э.д.с. и токов источника
считается направление от концов фазных
обмоток к их началам (по обходу треугольника
против часовой стрелки). Напряжения и
токи приемника и напряжения источника
направлены от начала каждой фазы к ее
концу (т.е. по часовой стрелке). При
соединении треугольником линейные и
фазные напряжения одинаковы
![]() .
Линейные токи направлены от источника
к приемнику и, как видно из схемы рис.
12, определяются через фазные токи в
соответствии с первым законом Кирхгофа
следующими выражениями:
.
Линейные токи направлены от источника
к приемнику и, как видно из схемы рис.
12, определяются через фазные токи в
соответствии с первым законом Кирхгофа
следующими выражениями:
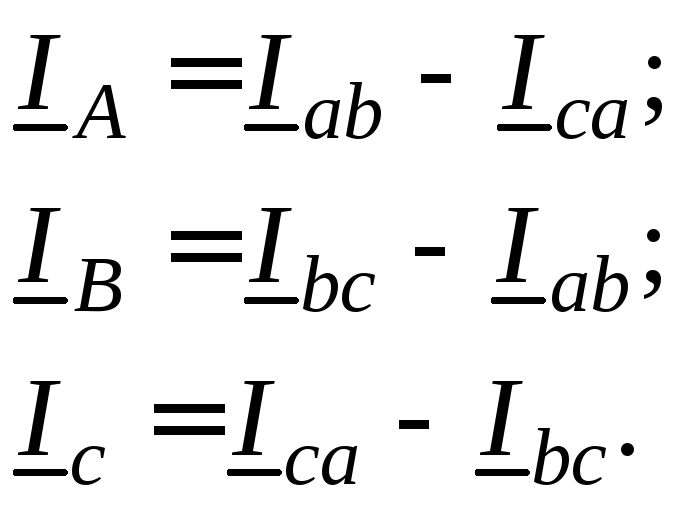
При
симметричной нагрузке
![]()
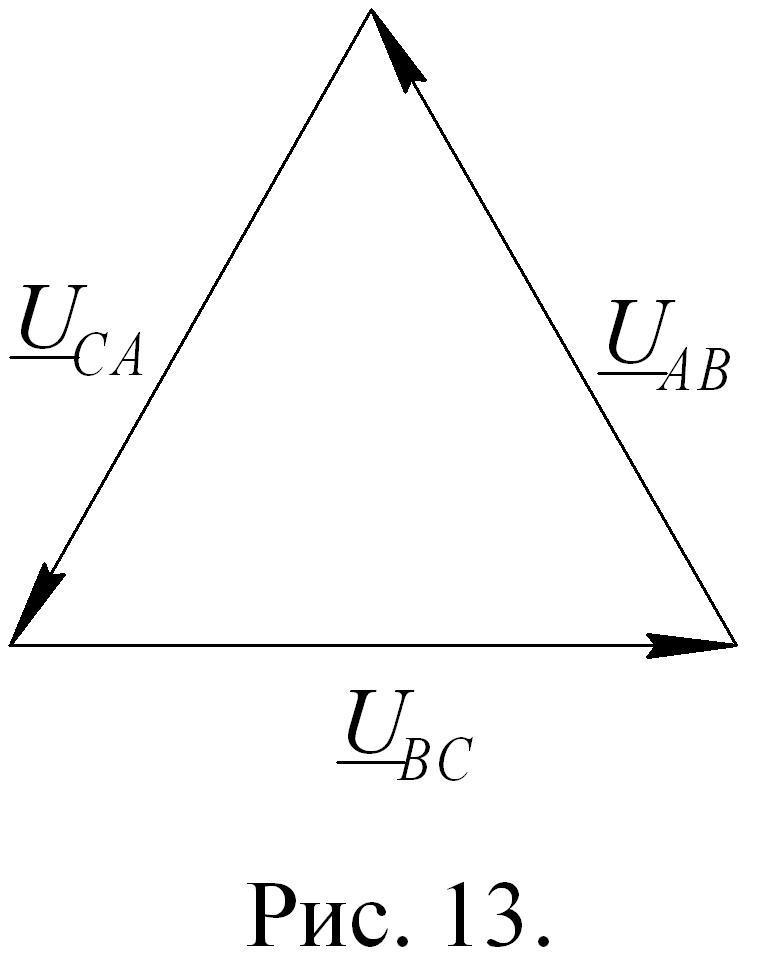
Векторная диаграмма напряжения источника строится по известному фазному (линейному) напряжению в виде равностороннего треугольника (рис. 13).
Если сопротивления линейных проводов считать равными нулю, то векторная диаграмма напряжений приемника будет одинаковой с векторной диаграммой источника.
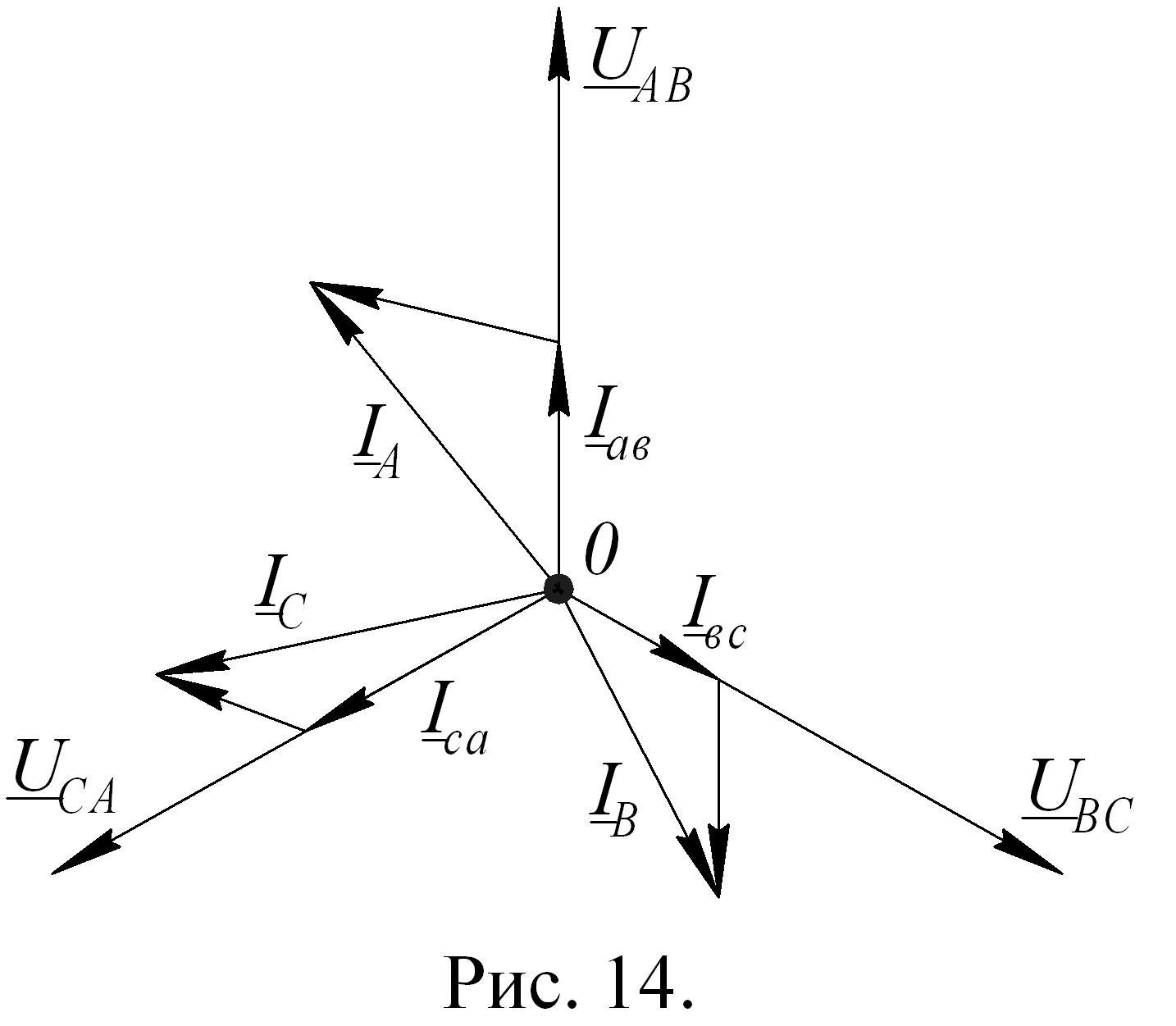
Для
построения векторной диаграммы токов
удобнее фазные напряжения приемника
изобразить в виде звезды, сохраняя при
этом сдвиг фаз напряжений. Векторы
фазных токов приемника откладывают от
точки 0 (рис. 14) с соответствующими
сдвигами по фазе относительно фазных
напряжений. Тогда линейные токи
определяются, согласно первому закону
Кирхгофа, векторами
![]() ,
,![]() ,
,![]() .
При активном характере нагрузки векторы
фазных токов совпадают по фазе с
соответствующими фазными напряжениями.
.
При активном характере нагрузки векторы
фазных токов совпадают по фазе с
соответствующими фазными напряжениями.
Задачи
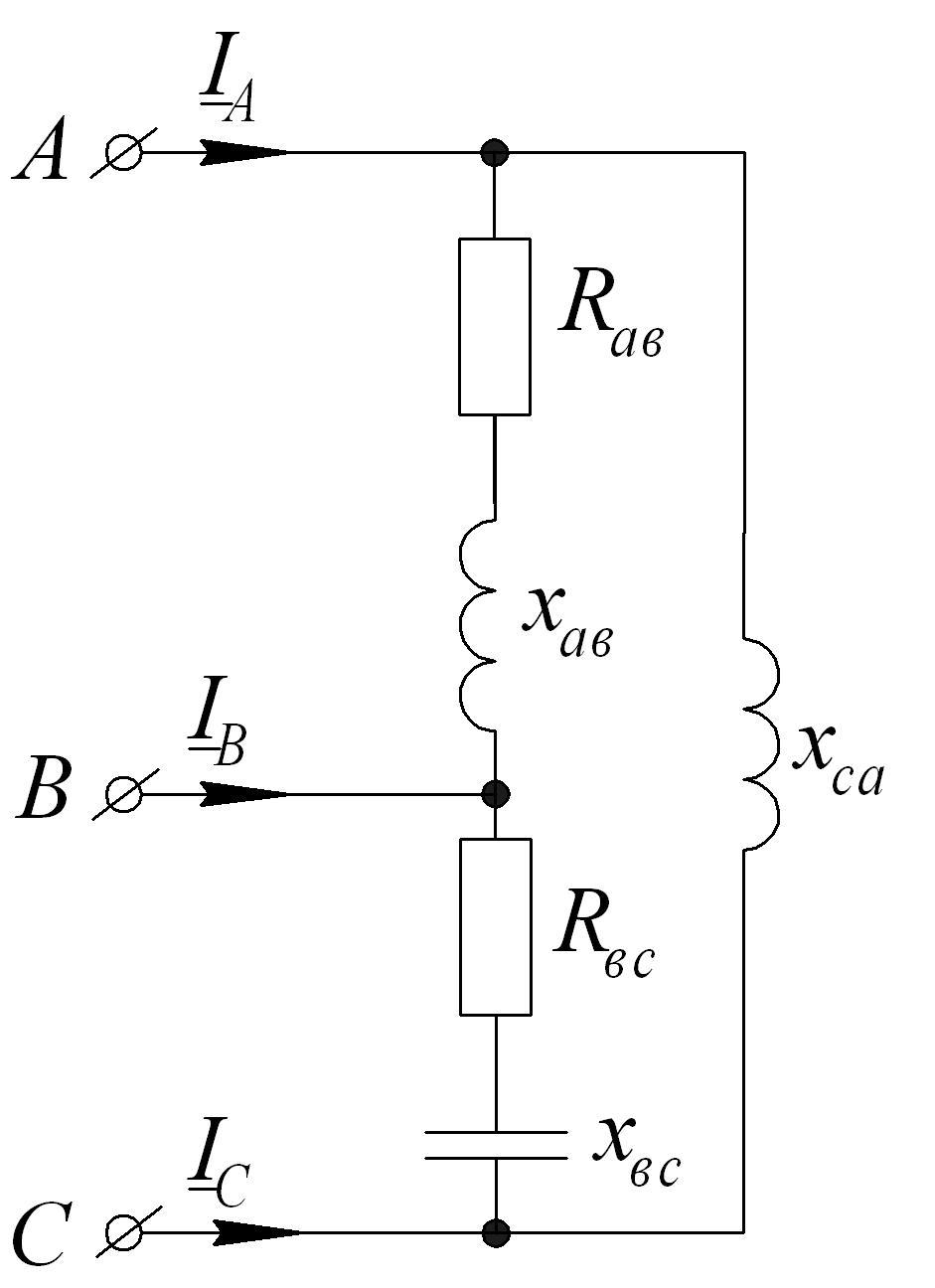
2.1.
Рассчитать трехфазную цепь, сопротивления
фаз которой
![]() B;
B;
![]() Ом;
Ом;![]() Ом;
Ом;![]() Ом;
Ом;![]() Ом;
Ом;![]() Ом.
Построить векторную диаграмму напряжений
и токов.
Ом.
Построить векторную диаграмму напряжений
и токов.
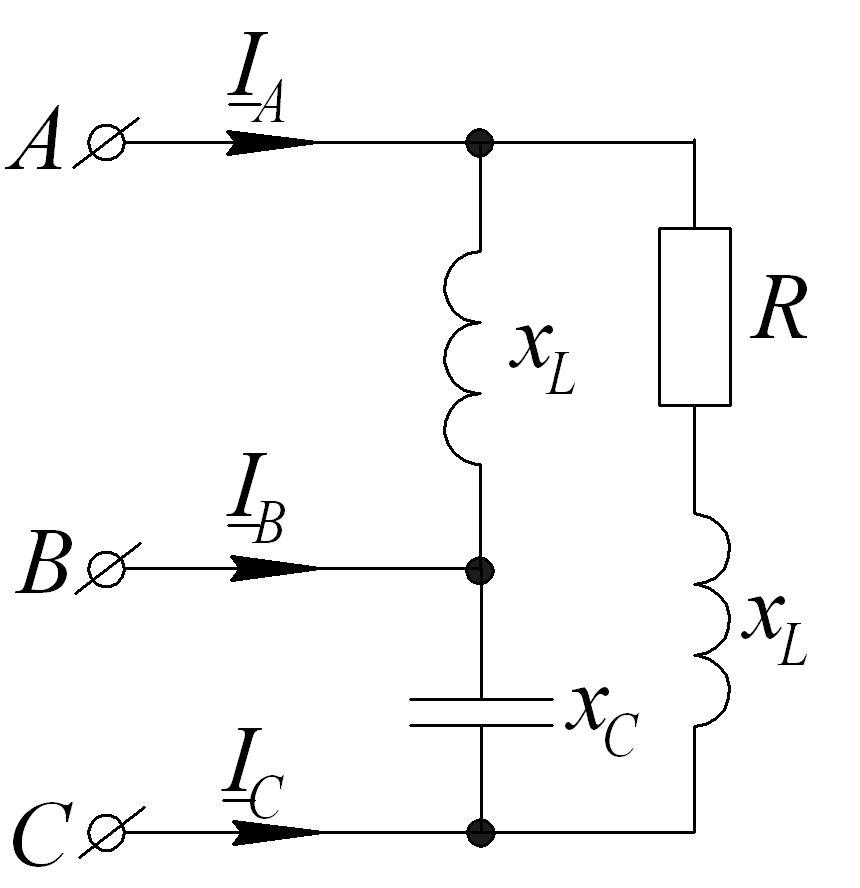
2.2.
Рассчитать трехфазную цепь, построить
векторную диаграмму напряжений и токов,
если
![]() Ом;
Ом;![]() .
.
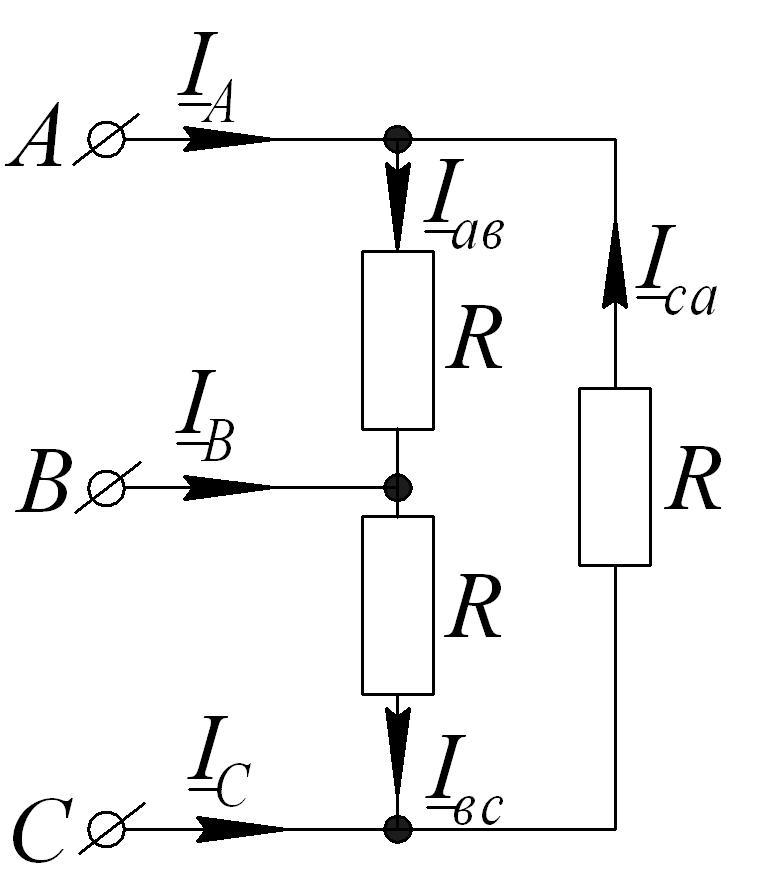
2.3.
Определить ток в фазе
![]() ,
при обрыве линейного провода В, если
,
при обрыве линейного провода В, если![]() Ом,
Ом,![]() В.
В.
2.4.
Определить линейный ток
![]() при обрыве провода А, если
при обрыве провода А, если![]() Ом;
показания вольтметра
Ом;
показания вольтметра![]() В.
В.

§3.9.3. Активная, реактивная и полная мощность трехфазной системы
Активной мощностью трехфазной системы называется сумма активных мощностей всех фаз приемника.
![]()
В симметричной трехфазной системе (при симметричном генераторе и приемнике) при любой схеме их соединений для каждой фазы мощности источника энергии и приемника одинаковы. Для каждой из фаз справедливо выражение
![]() ,
,
где - φ угол сдвига фаз между фазными напряжением и током.
Активная мощность системы в этом случае
![]()
Заменив действующее значение фазных тока и напряжения линейными при соединении источника энергии и приемника по схеме звезда т треугольник, получим одно и то же выражение для активной мощности симметричной трехфазной системы:
![]()
В общем случае реактивной мощностью трехфазной системы называется сумма реактивных мощностей всех фаз источника энергии, равная сумме реактивных мощностей всех фаз приемника.
Реактивная мощность симметричной трехфазной системы
![]() ,
,
или после замены действующих значений фазных тока и напряжения линейными
![]() .
.
Комплексной мощностью трехфазной системы называется сумма комплексных мощностей всех фаз источника энергии, равная сумме комплексных мощностей всех фаз приемника. Полная мощность симметричной трехфазной системы
![]() .
.
§ 3.9.4. Трехфазные цепи с несколькими приемниками в симметричном режиме
Расчет трехфазной цепи в симметричном режиме сводится к расчету одной фазы и проводится аналогично расчету обычной цепи синусоидального тока.
Пример 4.1.
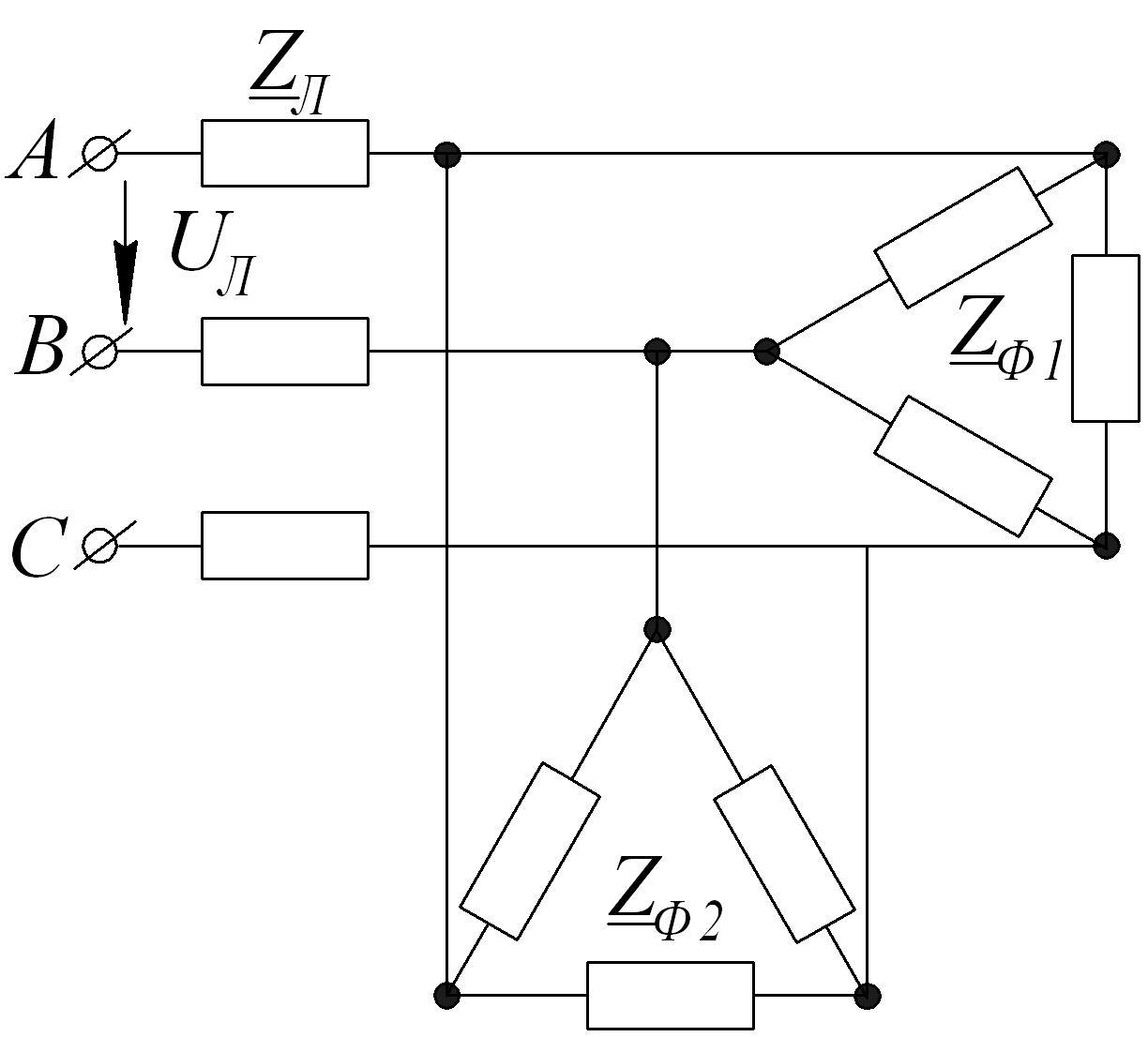
Дано:
![]() - линейное напряжение;
- линейное напряжение;
![]() - сопротивление
линии;
- сопротивление
линии;
![]() - фазное сопротивление
нагрузки 1;
- фазное сопротивление
нагрузки 1;
![]() - фазное сопротивление
нагрузки 2.
- фазное сопротивление
нагрузки 2.
Последовательность расчета:
1. Сопротивление двух треугольников, соединенных параллельно, необходимо заменить эквивалентным треугольником с сопротивлением фаз:
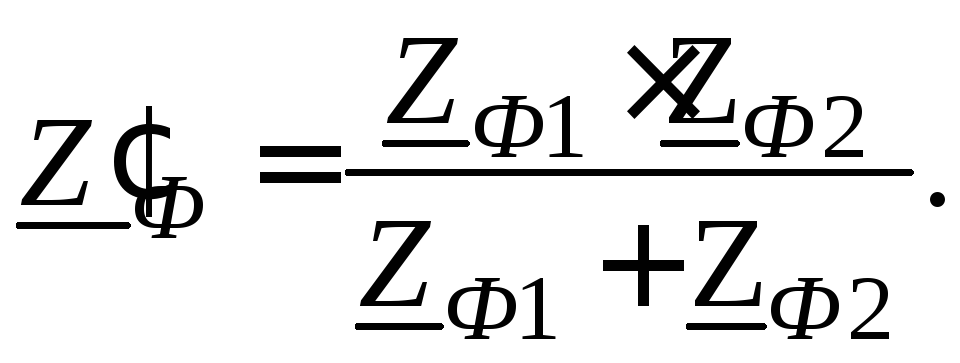
2. Полученный эквивалентный треугольник следует заменить эквивалентной звездой с сопротивлением фаз:
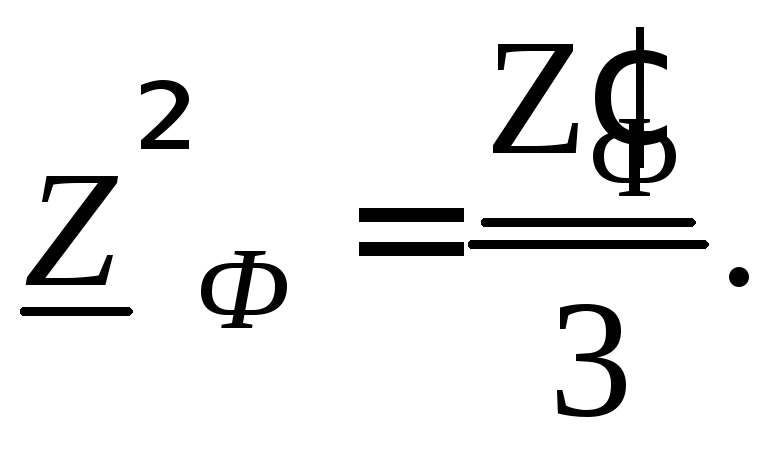
3. Определяют
фазные сопротивления эквивалентной
звезды с учетом
![]() :
:
![]()
4. Дальнейший расчет не требует применения комплексного метода. Достаточно определить действующее значение линейного тока
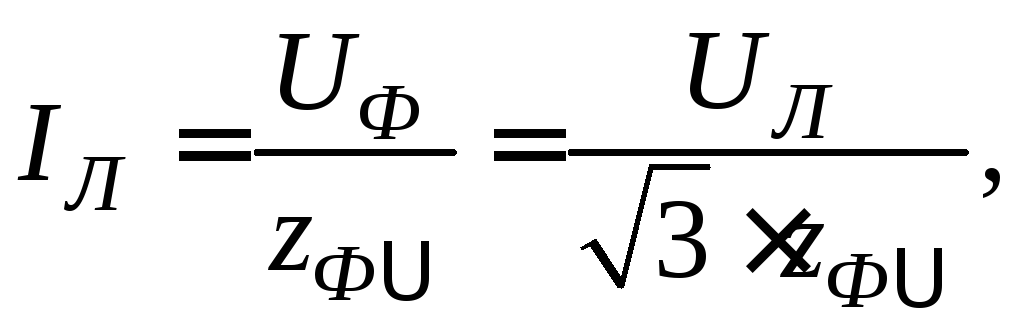
затем найти действующие значения фазного напряжения эквивалентной звезды приемника
![]()
и линейного напряжения приемника
![]() .
.
Действующие значения фазных токов приемников определяются по закону Ома:
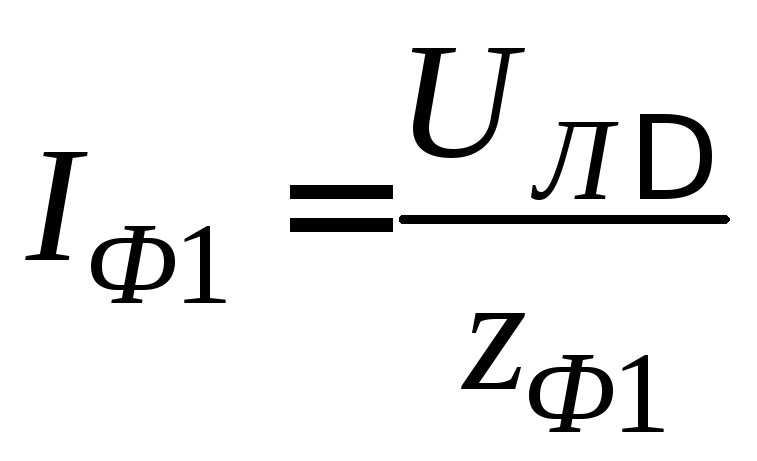 ,
,
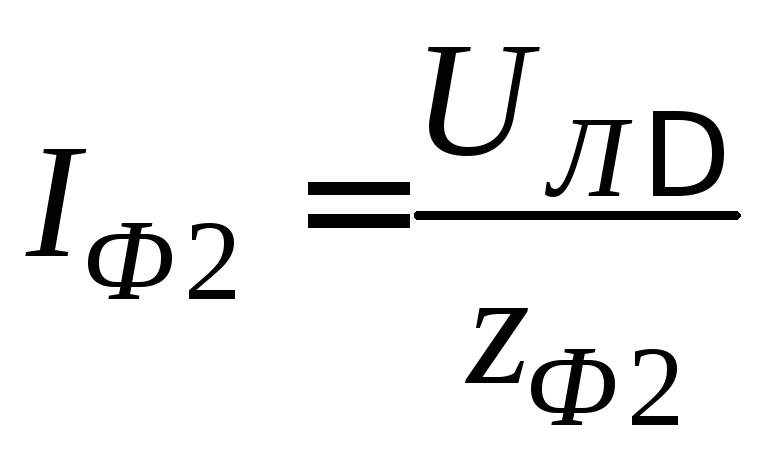 .
.
Задачи
4.1.
Определить
фазные и линейные токи и напряжения,
мощность, потребляемую приемником, если
![]() В;
В;
![]() Ом;
Ом;![]() Ом.
Построить векторные диаграммы напряжений
и токов.
Ом.
Построить векторные диаграммы напряжений
и токов.
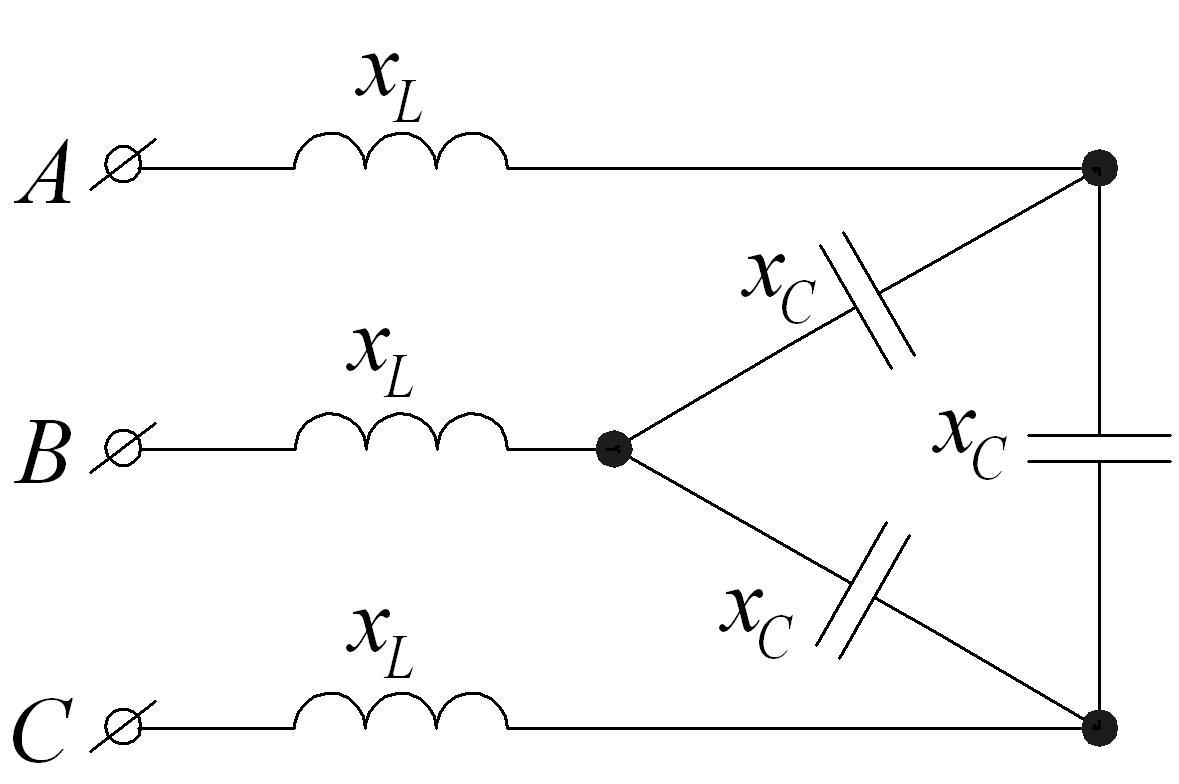
4.2.
Определить
фазные и линейные токи и напряжения,
мощность, потребляемую приемником, если
![]() В;
В;![]() Ом;
Ом;![]() Ом.
Построить векторные диаграммы напряжений
и токов.
Ом.
Построить векторные диаграммы напряжений
и токов.
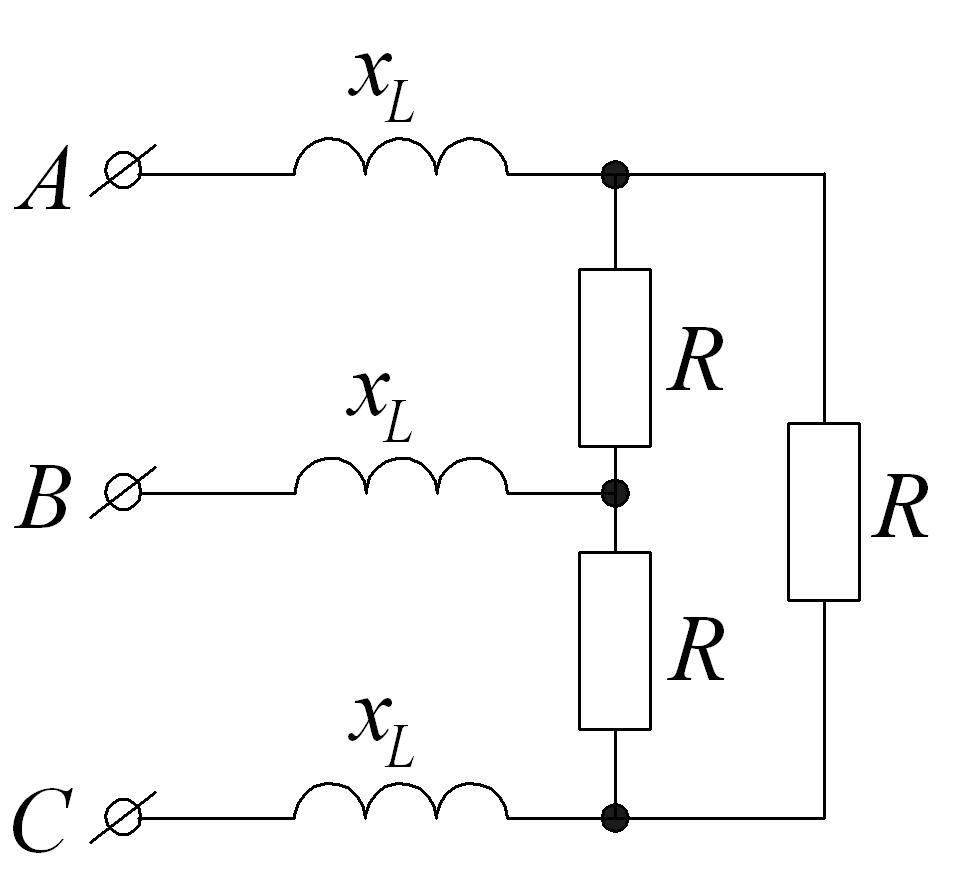
4.3.
Определить
фазные и линейные токи и напряжения,
мощность, потребляемую приемником, если
![]() В;
В;![]() Ом;
Ом;![]() Ом.
Построить векторные диаграммы напряжений
и токов.
Ом.
Построить векторные диаграммы напряжений
и токов.