
- •Основные элементы вычислений прямоугольных координат, дирекционных углов и дальностей.
- •Содержание. В 45 6101314 14 16 202526282930313436 3738394041 42 434445 45 46ведение.
- •Введение.
- •Основные правила вычислений.
- •Мера измерения углов. Перевод градусной меры в деления угломера и обратно.
- •Перевод градусной меры в деления угломера.
- •Переход от угловых минут и секунд к десятичным долям градуса и наоборот.
- •Зависимость между линейной и угловой величинами.
- •Азимуты и дирекционный угол.
- •Прямой и обратный дирекционный угол.
- •Определение величины горизонтального угла по дирекционным углам направлений, составляющих этот угол, и наоборот.
- •Переход от истинного азимута к дирекционному углу. Определение сближения меридианов.
- •Переход от магнитного азимута к дирекционному углу и обратно. Определение поправки буссоли по данным карты.
- •Изменение поправки буссоли при перемещении на местности в новый район.
- •Тригонометрические функции острого угла.
- •Решение треугольника.
- •Решение треугольника по двум углам и одной стороне.
- •Решение треугольника по двум сторонам и углу между ними.
- •Определение превышений и абсолютных высот.
- •Приведение наклонных расстояний к горизонту.
- •Определение расстояний засечкой с помощью базы.
- •Прямая геодезическая задача.
- •Пгз решают в следующей последовательности:
- •Обратная геодезическая задача.
- •Огз решают в следующей последовательности:
- •Заключение.
- •Приложения.
- •Т Приложение 5.Аблица натуральных значений тригонометрических функцийsin и cos.
- •За переход в смежную зону.
Тригонометрические функции острого угла.

Тригонометрическими функциями острого угла называются числовые значения взаимного отношения любых двух сторон прямоугольного треугольника. В зависимости от того, отношения каких сторон прямоугольного треугольника рассматриваются, тригонометрические функции носят названия: синус (sin), косинус (cos), тангенс (tg), котангенс (ctg) и др.
Синусомострого угла называется числовое значение отношения длины противолежащего катета к длине гипотенузы:
![]() (31)
(31)
Косинусомострого угла называется числовое значение отношения длины прилежащего катета к длине гипотенузы:
![]() (32)
(32)
Тангенсомострого угла называется числовое значение отношения длины противолежащего катета к длине прилежащего катета:
![]() (33)
(33)
Котангенсомострого угла называется числовое значение отношения длины прилежащего катета к длине противолежащего катета:
![]() (34)
(34)
Функции острых углов играют важную роль при решении многих математических и топогеодезических задач, однако их использование ограничено пределами изменений острых углов от 0(0-00) до 90(30-00). При топогеодезической привязке в системе определения дирекционных углов используются углы (направления) с пределами измерений до 360(60-00). Поэтому возникает необходимость распространения понятия тригонометрических функций на углы любой величины.
Тригонометрические функции любого произвольного угла можно выразить через значения тригонометрических функций острого угла (углаIчетверти, смотри рисунок 23). Учитывая такие преобразования, составлена "Таблица натуральных значений тригонометрических функций синусов и косинусов"(Приложение 6). По таблице можно определить тригонометрические функции синуса и косинуса, не приводя угол кIчетверти.
Решение треугольника.
С решением треугольника связаны все виды засечек. Решить треугольник, – это значит, определить неизвестные значения угловых и линейных элементов. Для решения треугольника необходимо знать значения трех любых его элементов, из них должна быть хотя бы одна сторона.
В практике топогеодезических работ привязка элементов боевого порядка засечками сводится к вычислению по известным двум углам и одной стороне третьего угла и двух других сторон или к вычислению по известным двум сторонам и углу между ними третьей стороны и двух углов.
Решение треугольника осуществляют по формулам соотношений его элементов, известных из курса тригонометрии.
Обозначив
в треугольнике АВС
(рис. 17) стороны
через
![]() ,
,
![]() и
и
![]() а углы через
А, В и
С, запишем
основные соотношения:
а углы через
А, В и
С, запишем
основные соотношения:
![]() (теорема
суммы углов); (35)
(теорема
суммы углов); (35)
![]() (теорема
синусов); (36)
(теорема
синусов); (36)
![]() (теорема
косинусов); (37)
(теорема
косинусов); (37)
![]() (теорема
тангенсов). (38)
(теорема
тангенсов). (38)
Рассмотрим применение данных теорем при решении треугольника.
Решение треугольника по двум углам и одной стороне.
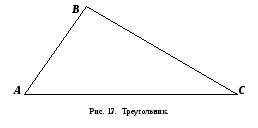
Последовательность решения:
Находят угол С из теоремы суммы углов по формуле
![]() или
или
![]() ; (39)
; (39)
Длины сторон
 и
и вычисляют по теореме синусов по формулам
вычисляют по теореме синусов по формулам

![]()
Контроль вычислений осуществляют по формуле
![]() (42)
(42)
