[Править]Правило фаз Гиббса

Рассмотрим теперь систему, вообще говоря, химически неоднородную (состоящую из нескольких веществ). Пусть   — число компонентов (веществ) в системе, а   — число фаз. Условие равновесия фаз для такой системы можно записать в виде системы из   уравнений:

Здесь   — химический потенциал для i-го компонента в j-й фазе. Он однозначно определяется давлением, температурой и концентрацией каждого компонента в фазе. Концентрации компонетнов не независимы (их сумма равна 1). Поэтому рассматриваемая система уравнений содержит   неизвестных (  — концентрации компонентов в фазах, плюс температура и давление).

Система разрешима, вообще говоря, если число уравнений не превышает числа неизвестных (система, не удовлетворяющая этому условию, также может быть разрешима, однако это исключительный случай, с которым в физике можно не считаться). Поэтому

• ,

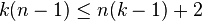отсюда

• ,

то есть число фаз в равновесной системе может превышать число компонентов не более, чем на два.

Последнее неравенство называется правилом фаз Гиббса. В частном случае для однокомпонентной (химически однородной системы) оно превращается в условие

• .

Термодинами́ческие потенциа́лы (термодинамические функции) — характеристические функции в термодинамике, убыль которых в равновесных процессах, протекающих при постоянстве значений соответствующих независимых параметров, равна полезной внешней работе.

Термин был введён Пьером Дюгемом, Гиббс в своих работах использовал термин «фундаментальные функции».

Выделяют следующие термодинамические потенциалы:

• внутренняя энергия

• энтальпия

• свободная энергия Гельмгольца

• потенциал Гиббса

• большой термодинамический потенциал

Содержание   [убрать] 1 Определения (для систем с постоянным числом частиц) 1.1 Внутренняя энергия 1.2 Энтальпия 1.3 Свободная энергия Гельмгольца 1.4 Потенциал Гиббса 2 Термодинамические потенциалы и максимальная работа 3 Каноническое уравнение состояния 4 Метод термодинамических потенциалов. Соотношения Максвелла 5 Системы с переменным числом частиц. Большой термодинамический потенциал 6 Потенциалы и термодинамическое равновесие 7 Литература

[править]Определения (для систем с постоянным числом частиц)

[править]Внутренняя энергия

Определяется в соответствии с первым началом термодинамики, как разность между количеством теплоты, сообщенным системе, и работой, совершенной системой над внешними телами:

.

[править]Энтальпия

Определяется следующим образом:

,

где   — давление, а   — объём.

Поскольку в изобарном процессе работа равна  , приращение энтальпии в квазистатическом изобарном процессе равно количеству теплоты, полученному системой.

[править]Свободная энергия Гельмгольца

Также часто называемый просто свободной энергией. Определяется следующим образом:

,

где   — температура и   — энтропия.

Поскольку в изотермическом процессе количество теплоты, полученное системой, равно  , то убыль свободной энергии в квазистатическом изотермическом процессе равна работе, совершённой системой над внешними телами.

Потенциал Гиббса

Также называемый энергией Гиббса, термодинамическим потенциалом, свободной энергией Гиббса и даже просто свободной энергией (что может привести к смешиванию потенциала Гиббса со свободной энергией Гельмгольца):

.

Термодинамические потенциалы и максимальная работа

Внутренняя энергия представляет собой полную энергию системы. Однако второе начало термодинамики запрещает превратить всю внутреннюю энергию в работу.

Можно показать, что максимальная полная работа (как над средой, так и над внешними телами), которая может быть получена от системы в изотермическом процессе, равна убыли свободной энергии Гельмгольца в этом процессе:

,

где   — свободная энергия Гельмгольца.

В этом смысле   представляет собой свободную энергию, допускающую преобразование в работу. Оставшаяся часть внутренней энергии может быть названа связанной.

В некоторых приложениях приходится различать полную и полезную работу. Последняя представляет собой работу системы над внешними телами, исключая среду, в которую она погружена. Максимальная полезная работа системы равна

где   — энергия Гиббса.

В этом смысле энергия Гиббса также является свободной.