
- •Министерство образования и науки
- •1. Введение
- •1.1. Вопросы организации изучения курса
- •1.2. Основные элементы геометрического моделирования
- •1.3. Условные обозначения и символы
- •1.4. Основы графического моделирования
- •Виды (способы) проецирования
- •1.5. Свойства ортогонального проецирования
- •1.6. Разновидности графических задач
- •Вопросы для самоконтроля
- •2. Получение обратимого чертежа, задание на нём точки
- •Вопросы для самоконтроля
- •3. Прямые линии на чертеже
- •3.1. Прямые частного положения на чертеже
- •3.2. Прямые общего положения на чертеже. Решение с ними метрических задач
- •Алгоритм решения
- •3.3. Определение по чертежу взаимного положения прямой и точки
- •Примеры решения задач
- •Алгоритм решения
- •3.4. Определение по чертежу взаимного положения прямых линий
- •1. Определение по чертежу параллельных прямых линий
- •2. Определение по чертежу пересекающихся прямых линий (позиционные задачи)
- •2.1. Определение по чертежу перпендикуляно пересекающихся прямых (комплексные задачи)
- •3. Определение по чертежу скрещивающихся прямых (позиционные задачи)
- •4. Определение по чертежу перпендикулярно скрещивающихся прямых (комплексные задачи).
- •Примеры решения задач о взаимном положении прямых
- •Вопросы для самоконтроля
- •4.Кривые линии на чертеже
- •Свойства проекций кривых линий
- •Вопросы для самоконтроля
- •5. Плоские поверхности на чертеже
- •5.1. Разновидности плоских поверхностей
- •5.2. Определение по чертежу положения плоскостей относительно основных плоскостей проекций
- •Алгоритм решения
- •Алгоритм решения
- •5.4. Определение по чертежу взаимного положения плоскостей и прямых линий
- •5.4.1. Параллельные прямая и плоскость на чертеже
- •Алгоритм решения
- •5.4.2. Параллельные плоскости на чертеже
- •Алгоритм решения:
- •5.4.3. Пересечение плоской поверхности с прямой линией на чертеже
- •Решение задач 1.Гпз. 1 (,) Алгоритм решения
- •Алгоритм решения
- •Решение задач 1.Гпз . 2 ( , не) Алгоритм решения
- •Алгоритм решения
- •Алгоритм решения
- •Алгоритм решения
- •Алгоритм решения
- •5.4.4. Пересечение плоских поверхностей на чертеже
- •Алгоритм решения
- •5.4.5. Взаимно перпендикулярные прямая линия и плоскость общего положения на чертеже
- •Алгоритм решения
- •5.4.6. Взаимно перпендикулярные плоскости общего положения на чертеже
- •Алгоритм решения
- •Вопросы для самоконтроля
- •6. Кривые поверхности на чертеже
- •6.1. Основные разновидности кривых поверхностей
- •1. Кривые поверхности с прямолинейными образующими
- •1.1.Цилиндрическая поверхность
- •1.2. Коническая поверхность
- •1.3. Поверхности вращения с прямолинейными образующими
- •1.5. Винтовые поверхности с прямолинейными образующими (геликоиды)
- •2. Поверхности вращения с криволинейной образующей
- •Частные разновидности поверхностей вращения
- •1. Торовая поверхность
- •Разновидности торовых поверхностей:
- •2. Эллипсоид вращения
- •2. Каналовые поверхности
- •6.2. Принадлежность кривой поверхности её элементов на чертеже
- •6.3. Пересечение кривой поверхности с прямой
- •Алгоритм решения
- •Алгоритм решения
- •Алгоритм решения
- •Решение
- •6.5. Взаимное пересечение кривых поверхностей на чертеже (2.Гпз)
- •Алгоритм решения
- •Алгоритм решения:
- •Алгоритм решения
- •Алгоритм решения
- •Возможны следующие четыре варианта
- •Решение
- •Особенности решения задач на пересечение
- •Решение
- •Вопросы для самоконтроля
- •7. Решение задач с преобразованием чертежа
- •7.1. Решающие положения прямых линий и плоскостей на чертеже Решающие положения для прямых линий
- •Решающие положения для плоскостей
- •7.2. Преобразование чертежа методом введения дополнительных ортогональных плоскостей проекций
- •Решение первой задачи
- •Решение второй задачи
- •Решение первой задачи
- •Решение второй задачи
- •Вопросы для самоконтроля
- •8. Конструктивные задачи графического моделирования
- •8.1. Примеры конструктивных задач
- •Решение
- •Алгоритм построения
- •Алгоритм построения
- •9.2. Построение развёрток кривых поверхностей
- •Алгоритм построения
- •Алгоритм построения
- •Алгоритм построения
- •Алгоритм построения
- •10. Построение аксонометрических изображений
- •11. Библиографический список
Алгоритм построения
Поверхность
развёртываема. Её развёртка представляет
собой прямоугольник высотой h
и с основанием,
равным длине окружности основания
цилиндра (2![]() r).
r).







![]() Развёртка
Развёртка
 цилиндра
цилиндра
![]() h
h





 2
2![]() r
r



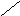

 r
r
![]()
Рис. 9.3
Пример
2 (рис.
9.4). Построить развёртку конуса вращения
![]() с радиусом окружности основания
r
и длиной образующей
l
.
с радиусом окружности основания
r
и длиной образующей
l
.
Алгоритм построения
Поверхность
развёртываема. Развёртка конуса вращения
представляет собой сегмент (вершина
S)
радиусом R
= l
и с углом при вершине сегмента
![]() = 2
= 2![]() r
/ R
(рад).
r
/ R
(рад).
 S
S![]()




![]() l
l![]() Развёртка
конуса
Развёртка
конуса ![]()
 S
S







 R
= l
R
= l



 S
S![]()
![]() =
=
![]()

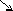


 L
=
L
=![]() R
= 2
R
= 2![]() r
r
r

![]()
Рис. 9.4
Пример
3 (рис.
9.5). Построить развёртку конуса общего
вида
![]() ,
основание которого представляет собой
горизонтально расположенную окружность
m
.
,
основание которого представляет собой
горизонтально расположенную окружность
m
.
Алгоритм построения
Поверхность развёртываема, но поскольку образующие конуса имеют переменную длину, то для построения развёртки используют приближённый метод, при котором развёртка конуса заменяется развёрткой вписанной n-гранной пирамиды.






 S
S![]()
 ив
|S4|
ив
|S4|
 4
4![]()



 5
5![]()







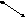





 1
1![]() 4
4![]()





![]()







 S
S![]()
5![]()




 1
1![]() 2
2![]() 4
4![]()
3![]()

 S
S![]()




 1
1![]()




 ив
2
ив
2![]()
 3
3![]()
Полуразвёртка
конуса
![]()
 4
4![]()
5![]()
Рис. 9.5
Пример
4 (рис.
11.6). Построить развёртку цилиндра общего
вида ![]() ,
у которого плоскость одного основания
(окружности) занимает горизонтальное
положение, а плоскость другого –
профильное.
,
у которого плоскость одного основания
(окружности) занимает горизонтальное
положение, а плоскость другого –
профильное.

 Полуразвёртка
4
Полуразвёртка
4![]()
 цилиндра
цилиндра
![]()
3![]()


2![]()


 2
2![]()


 1
1![]() =
1
=
1![]() 3
3![]() 4
4![]()






















![]()






















1![]() 4
4![]()



 3
3![]()
![]() 2
2![]()
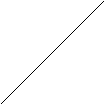
Рис. 9.6
Алгоритм построения
Поверхность развёртываема. Однако образующие цилиндра имеют переменную длину, поэтому развёртку строят приближенным методом, заменяя развёртку цилиндра развёрткой вписанной в цилиндр n - гранной призмы.
10. Построение аксонометрических изображений
Аксонометрическое проецирование обладает простотой построения изображения и его наглядностью. «Аксонометрия» - с греческого языка означает «измерение по осям». Суть этого метода проецирования (рис. 10.1): объект относят к некоторой системе координат, а затем вместе с координатной системой параллельно проецируют его на плоскость чертежа.



 z
z![]()
![]()
A![]()


 z
O
z
O![]()



 A
A![]() y
y![]()



 A
A
A
A![]()

 x
x![]()

 O
O
A![]()

x
A![]() y
y
Рис. 10.1
При
аксонометрическом проецировании
изображение точек на чертеже, по существу,
фиксирует их положение относительно
центра О
принятой
системы координат. Это и делает такой
чертёж обратимым. Отрезки координатных
осей при их проецировании на плоскость
чертежа искажаются в зависимости от
направления вектора проецирования по
отношению к координатной системе, с
одной стороны, и к плоскости чертежа, с
другой. При этом угол между плоскостью
чертежа и вектором проецирования может
быть равен 90![]() (прямоугольная аксонометрия) или не
равен 90
(прямоугольная аксонометрия) или не
равен 90![]() (косоугольная аксонометрия). В
машиностроении принята прямоугольная
аксонометрия. В прямоугольной аксонометрии
при проецировании отрезки осей координат
изменяют свою длину. Поэтому вводят
понятие «коэффициент искажения» оси,
который определяют отношением длины
проекции отрезка оси к его истинной
длине:
(косоугольная аксонометрия). В
машиностроении принята прямоугольная
аксонометрия. В прямоугольной аксонометрии
при проецировании отрезки осей координат
изменяют свою длину. Поэтому вводят
понятие «коэффициент искажения» оси,
который определяют отношением длины
проекции отрезка оси к его истинной
длине:
K![]() =
=
![]() ;
K
;
K![]() =
=
![]() ;
K
;
K![]() =
=
![]() .
.
В зависимости от соотношения коэффициентов искажения осей аксонометрические проекции могут быть:
изометрические
(K![]() =
K
=
K![]() =
K
=
K![]() );
);
диметрические
(K![]() =
K
=
K![]()
![]() K
K![]() );
);
триметрические
(K![]()
![]() K
K![]()
![]() K
K![]() ).
).
В машиностроении (согласно рекомендациям ГОСТ 2.317-69) используют прямоугольную изометрию или прямоугольную диметрию.
В прямоугольной изометрии коэффициенты искажения по осям:
K![]() =
K
=
K![]() =
K
=
K![]() =
0,85.
=
0,85.
Однако изометрическую проекцию строят без сокращения размеров по осям, что приводит к увеличению изображения против оригинала в 1,22 раза.
В прямоугольной диметрии коэффициенты искажения по осям:
K![]() =
K
=
K![]() =
0,95; K
=
0,95; K![]() =
0,47.
=
0,47.
При реальном построении проекций рекомендуется принимать:
K![]() =
K
=
K![]() =
1; K
=
1; K![]() =
0,5,
=
0,5,
при этом изображение увеличивается против оригинала в 1,06 раза.
Расположение осей координат в изометрии приведено на рис. 10.2, а в диметрии – на рис. 10.3.
Окружность в аксонометрии изображается в виде эллипса, который удобно строить с помощью параллелограмма, отображающего квадрат, описывающий окружность.
В изометрии (рис. 10.4) эллипсы на всех координатных плоскостях одинаковы между собой.

 z
z

 120
120![]() 120
120![]()






x y
Рис. 10.2

 z
z
7![]() 10
10![]()



8 8






 1
1
 x
41
x
41![]() 25
25![]()
7
y
Рис. 10.3
Описанный квадрат



 z
z






















 x
x



 x
y
x
y
y
Окружность на плоскости
Рис. 10.4
В диметрии (рис. 10.5) на плоскостях XY и ZY эллипсы одинаковы между собой и отличаются от эллипса на плоскости XZ .

 Точки эллипса
Точки
эллипса
Точки эллипса
Точки
эллипса



 z
z
z
z

























 x
x
x
x




 y
y
y
Рис. 12.5
Согласно рекомендациям ГОСТа при выполнении аксонометрических чертежей принято эллипсы заменять овалами. На рис. 10.6, 10.7 и 10.8 приведены способы построения овалов на координатных плоскостях при изометрии и диметрии.
 z
z




 O
O![]()



 O
O![]()







 O
O![]()

 x
y
x
y
O![]()
Рис. 10.6
 z
z














 O
O![]()
 O
O![]()






 x
x




y

Рис. 10.7
 z
z




O![]()



 O
O![]()











 x
x
 y
y
Рис. 10.8
Техника построения аксонометрического изображения сводится к умению строить следующие элементы изображаемого объекта.
1. Точки строят по их координатам.
2. Линии строят по их точкам.
2.1. Прямые линии строят по 2-м точкам или по 1-й точке и известному направлению.
2.2. Кривые линии строят по многим точкам, достаточным для их качественного воспроизведения.
Примечание.
Окружности, трансформируемые на чертеже в эллипс, строят с помощью овалов. Для того чтобы при построении аксонометрии иметь координаты точек изображаемого объекта (детали), предварительно строят обычный двух картинный чертёж детали и условно привязывают к ней систему координат.
Закрытые поверхности детали условно раскрывают путём выреза её части 2-мя взаимно перпендикулярными (координатными) плоскостями.
На рис. 10.9 приведён пример построения изометрии полой цилиндрической детали (втулки).

 z
z![]() z
z![]()






 O
O![]() =
x
=
x![]()

 x
x![]() y
y![]()








O![]() =
y
=
y![]()
z























 y
y







 x
x
Рис. 10.9
