
- •Министерство образования и науки
- •Оглавление
- •Контрольные решения задач
- •Упражнение 1.7
- •Упражнение 1.8
- •Тема 2. Прямые линии на чертеже. Взаимное положение прямых и точек Упражнение 2.1
- •Упражнение 2.2
- •Упражнение 2.10
- •Упражнение 2.11
- •Упражнение 2.12
- •Упражнение 2.13
- •Упражнение 2.14
- •Упражнение 2.15
- •Упражнение 2.16
- •Упражнение 2.17
- •Тема 3. Решение метрических задач с прямой линией общего положения Упражнение 3.1
- •Упражнение 3.2
- •Упражнение 3.3
- •Упражнение 3.4
- •Упражнение 3.5
- •Упражнение 9.2
- •Упражнение 9.3
- •Упражнение 9.4
- •Упражнение 9.5
- •Упражнение 9.6
- •Упражнение 11.13
- •Упражнение 18.2
Тема 3. Решение метрических задач с прямой линией общего положения Упражнение 3.1
Решение
Для
определения угла
![]() методом «прямоугольного треугольника»
строим горизонтальную проекцию отрезка,
которую принимаем в качестве первого
катета.
методом «прямоугольного треугольника»
строим горизонтальную проекцию отрезка,
которую принимаем в качестве первого
катета.






 А
А![]() A
A![]()


 В
В![]() В
В![]()
 B
B![]() 2k
2k






1k


![]() B
B![]()
A![]()
и.в. АВ
Упражнение 3.2
Решение

 B
B![]()






 C
C![]() 2k
2k
 20
мм
B
20
мм
B![]()

 A
A![]() C
C![]()


A![]()
C![]()
B![]()
Упражнение 3.3
Решение
В![]() B
B![]()







 2k
2k
![]()


 1k
A
1k
A![]()


А![]() 20
мм
A
20
мм
A![]()
Упражнение 3.4
Решение
Для
решения задачи на заданной прямой m
произвольно выбираем точку С
и на базе профильной проекции отрезка
АС
строим прямоугольный треугольник,
определяя его истинную длину и угол
наклона прямой m
к плоскости
![]() .
Здесь же строим и отрезок АВ
длиной 20
мм, с помощью которого определяем
профильную и фронтальную проекции т.
В.
.
Здесь же строим и отрезок АВ
длиной 20
мм, с помощью которого определяем
профильную и фронтальную проекции т.
В.
m![]() m
m![]()






 C
C![]() C
C![]() 2k
2k


 B
B![]()




 B
B![]()
![]() C
C![]()



A![]() 2k A
2k A![]() B
B![]() 1k
1k
и.в. АВ = 20 мм
Упражнение 3.5
Решение
Возможны 2 решения: точка В может располагаться и ниже точки А .

 В
В![]()


 А
А![]()
 2k
2k


 В
В![]()

 30
30![]()
А![]() В
В![]()
Упражнение 3.6
Решение

 1k
= А
1k
= А![]() B
B![]() 2k
= 15 мм
2k
= 15 мм







 B
B![]()


и.в. АВ =30 мм

 А
А![]()
 А
А![]()





 10
мм В
10
мм В![]()
Упражнение 3.7
Решение
А![]() А
А![]()






 60
60![]()


 1k
и.в.
АВ
= 30 мм
1k
и.в.
АВ
= 30 мм





 15
мм
15
мм
 B
B![]() B
B![]()
B![]()
2k
Тема 4. Взаимно перпендикулярные прямые линии на чертеже
Упражнение 4.1
Решение

 f
f![]()


 a
a![]()
 A
A![]()




 f
f![]() A
A![]()
a![]()
Упражнение 4.2
Решение
Как видно из чертежа прямая n перпендикулярно пересекающаяся с прямой a и перпендикулярно скрещивающаяся с прямой b .

 n
n![]() n
n![]()









 b
b![]() b
b![]()

 a
a![]()
M![]() =
a
=
a![]() M
M![]()
Упражнение 4.3
Решение
Расстояние
между прямыми a
и
b
– это их
общий перпендикуляр АВ
= | A![]() B
B![]() |
.
|
.

 f
f![]()



 B
B![]()

 и.в.
АВ
и.в.
АВ

 a
a![]() =
A
=
A![]() b
b![]()
a![]() b
b![]()





 f
f![]()
A![]() B
B![]()
Упражнение 4.4
Решение

 B
B![]() B
B![]() и.в.
АВ
и.в.
АВ











 1k
1k

 2k
2k
A![]() p
p![]() p
p![]() A
A![]()
 2k
2k
Упражнение 4.5
Решение




 n
n![]()
 A
A![]()
h![]() a
a![]()











h![]() A
A![]() a
a![]() ||
h
||
h![]()


n![]()
Упражнение 4.6
Решение
 и.в.
АВ
А
и.в.
АВ
А![]() А
А![]()










В![]()

 B
B![]()
a![]() а
а![]()
Упражнение 4.7
Решение


 A
A![]()

B![]()




 h
h![]() 2k
2k






 B
B![]()


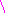
 и.в.
АВ
= 30 мм
и.в.
АВ
= 30 мм

h![]() 1k
A
1k
A![]()
Упражнение 4.8
Решение
Второе решение, это когда точка В расположена правее профильной прямой p .
 2k
2k



 a
a![]() p
p![]() p
p![]() a
a![]()




 B
B![]() B
B![]()

 2k
2k


 1k
1k




A![]() A
A![]()
![]() =30
=30![]()
Упражнение 4.9
Решение
B![]() h
h![]()




 2k
2k

А![]() C
C![]() h
h![]()








 А
А![]()


 и.в.
ВС
= 25 мм
C
и.в.
ВС
= 25 мм
C![]()

 1k
h
1k
h![]()
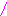

 2k
В
2k
В![]()
h![]()
Упражнение 4.10
Решение





 A
A![]() h
h![]()
 f
f![]()

 B
B![]()
h![]()
 2k
2k



 A
A![]()
 1k
1k




 и.в.
АВ
и.в.
АВ
B![]() f
f![]()
Тема 5. Кривые линии на чертеже
Упражнение 5.1.
Решение
Характер кривой линии m определяем с помощью двух хорд, соединяющих 4 произвольно выбранные точки этой кривой: поскольку хорды занимают скрещивающееся положение (не лежат в плоскости), следовательно, заданная линии m – пространственная.


 m
m![]()









m![]()
Упражнение 5.2
Решение



 A
A![]() F
F![]()





 E
E![]()


 B
B![]() C
C![]() D
D![]()




 C
C![]() D
D![]()

B![]()

E![]()

A![]()
F![]()
Упражнение 5.3
Решение






 F
F![]()
 B
B![]()








 C
C![]()





 A
A![]() E
E![]() m
m![]()
D![]()
 m
m![]()

A![]() B
B![]() C
C![]() D
D![]() E
E![]() F
F![]()
Упражнение 5.4
Решение
 2
2![]() = (2
= (2![]() )
1
)
1![]() 2
2![]() = (2
= (2![]() )
m
)
m![]()

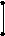
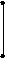




 1
1![]()





 2
2![]() 2
2![]()


 R
R

r





2![]() 2
2![]() m
m![]()
Упражнение 5.5
Решение
С
помощью концентрических окружностей,
построенных на осях эллипса, и секущей
прямой k
определяем дополнительные точки эллипса
(например, точки 5![]() и 6
и 6![]() ),
после чего проводим эллипс
m.
),
после чего проводим эллипс
m.
 k
k![]()


 6
6![]() 1
1![]() 5
5![]()








 4
4![]() 2
2![]()




m![]() 6
6![]() 3
3![]() 5
5![]()
 m
m![]()



4![]() 1
1![]() = ( 3
= ( 3![]() )
2
)
2![]()
6![]() = ( 6
= ( 6![]() )
5
)
5![]() = ( 5
= ( 5![]() )
)
Упражнение 5.6
Решение
m![]()




 O
O![]()










 O
O![]()



 m
m![]()
Упражнение 5.7
Решение
 A
A![]() m
m![]() B
B![]() A
A![]() =
(
B
=
(
B![]() )
)






































 Ход
m
Ход
m![]()

Упражнение 5.8
Решение

 m
m![]() B
B![]() B
B![]() A
A![]()














 A
A![]()















































 Ход
m
Ход
m![]()

Тема 6. Плоские поверхности на чертеже
Упражнение 6.1
Решение
Второе
решение, когда грань
![]() (ABC)
наклонена к плоскости
(ABC)
наклонена к плоскости
![]() в другую сторону.
в другую сторону.
 С
С![]() C
C![]()







 В
В![]() B
B![]()

 А
А![]() А
А![]()
![]() = 30
= 30![]()
Упражнение 6.2
Решение
 f
f![]()


 A
A![]() h
h![]()




 A
A![]() f
f![]()
h![]()
Упражнение 6.3
Решение





 B
B![]() B
B![]()




 C
C![]() A
A![]()







 A
A![]() C
C![]()





 A
A![]()

 B
B![]()
 C
C![]()
Упражнение 6.4
Решение





 D
D![]() D
D![]()




 A
A![]() A
A![]()

 C
C![]()



C![]()


 B
B![]() B
B![]()
Упражнение 6.5
Решение


 (B
(B![]() )
=
C
)
=
C![]()
 (A
(A![]() )
= D
)
= D![]() и.в.
AB
и.в.
AB




 A
A![]() B
B![]()

и.в. BC
 D
D![]() C
C![]()
Упражнение 6.6
Решение

 A
A![]()



B![]()

 D
D![]()
 C
C![]()



D![]() A
A![]() C
C![]() B
B![]()
Упражнение 6.7
Решение
A![]() A
A![]()








 D
D![]() D
D![]()








 S
S![]() S
S![]()








B![]() B
B![]()

C![]() C
C![]()
Упражнение 6.8
Решение









l![]()
A![]() B
B![]() D
D![]() C
C![]()







D![]()




 C
C![]()



 A
A![]()

 B
B![]()
 l
l![]()

Упражнение 6.9
Решение
S![]()




 20
мм
20
мм
A![]() B
B![]() C
C![]()







B![]()







S![]()


 A
A![]()

 C
C![]()
Тема 7. Принадлежность плоской поверхности её элементов на чертеже. Решение метрических задач
Упражнение 7.1
Решение


 a
a![]() =
=
![]() a
a![]()

Упражнение 7.2
Решение
 a
a![]() B
B![]() b
b![]()










 c
c![]() ||
b
||
b![]()

 A
A![]()

 2k
2k



A![]()





 c
c![]() ||
b
||
b![]()



 2k
2k
 b
b![]()

a![]() B
B![]() и.в.
АВ
и.в.
АВ
Упражнение 7.3
Решение

 A
A




![]() A
A![]()


 d
d![]() d
d![]()






 D
D![]() D
D![]()



 B
B![]() B
B![]()

C![]() C
C![]()
Упражнение 7.4
Решение

 A
A![]()
 и.в.
АВ
и.в.
АВ







 A
A![]() 2k
2k





 B
B![]() b
b![]()

 a
a![]()




 a
a![]()


 A
A![]()
 b
b![]()
B![]()
Упражнение 7.5
Решение
 m
m![]() C
C![]()















 A
A![]() B
B![]()









 A
A![]() C
C![]()
m![]()
B![]()
Упражнение 7.6
Решение











 A
A![]() A
A![]()




 n
n![]() m
m![]() m
m![]() n
n![]()






C![]() B
B![]() B
B![]() C
C![]()
Упражнение 7.7
Решение



 D
D![]()










![]() B
B![]() C
C![]()






 A
A![]() L
L![]() M
M![]()








 l
l![]()






 l
l![]()






 A
A![]() L
L![]() M
M![]()

![]() B
B![]()
Упражнение 7.8
Решение

 C
C![]() (M
(M![]() )
M
)
M![]()

















B![]()





 B
B
![]()





 A
A![]() A
A![]()

 l
l![]() l
l![]()
Упражнение 7.9
Решение




 C
C![]() C
C![]()






 B
B![]() B
B![]()










 M
M![]() M
M![]()




A![]() 25
мм
A
25
мм
A![]()
Упражнение 7.10
Решение
S![]() S
S![]()














B![]() B
B![]()
D![]() D
D![]()





 C
C![]()



A![]() A
A![]()
Упражнение 7.11
Решение
 h
h![]() g
g![]() B
B![]() g
g![]() f
f![]()



















 A
A![]() C
C![]()







 A
A![]() C
C![]()








h![]() g
g![]() B
B![]() g
g![]() f
f![]()
Упражнение 7.12
Решение
q![]()
 B
B![]()





 h
h![]() A
A![]()

 C
C![]()




 q
q![]() 2k
2k



 1k
h
1k
h![]()
![]()
A![]()
Упражнение 7.13
Решение
 B
B![]() B
B![]()





 n
n![]()
![]() f
f![]() f
f![]() n
n![]()


 1k
1k
2k

Упражнение 7.14
Решение

 g
g![]() h
h![]()






 A
A![]() f
f![]()







 A
A![]() g
g![]() h
h![]()



![]()





 1k
1k
 2k
f
2k
f![]()
Упражнение 7.15
Решение

 f
f![]() f
f![]()




 q
q![]() q
q![]()

 2k
2k











![]()

 1k
1k


g![]() g
g![]()

p![]() p
p![]()
Упражнение 7.16
Решение






 B
B![]() B
B![]()




 2k
C
2k
C![]() C
C![]()








![]()
 1k
1k





 A
A![]() A
A![]()

A![]() B
B![]() C
C![]() =и.в.
ABC
=и.в.
ABC
A![]()
Упражнение 7.17
Решение




 A
A![]() f
f![]() A
A![]() g
g![]()












B![]() B
B![]()














![]()
 g
g![]()






 C
C![]() C
C![]()
f![]()
A![]() B
B![]() C
C![]() =и.в.
ABC B
=и.в.
ABC B![]()
Упражнение 7.18
Решение


 S
S![]()













 S
S![]()



![]()
![]()





 A
A![]() B
B![]() C
C![]()


A![]() S
S![]() C
C![]()







B![]()
Упражнение 7.19
Решение
A![]()

 A
A![]()










и.в.
AA![]()
A![]() B
B![]() C
C![]()














 B
B![]()









 C
C![]()



![]()
![]()

 A
A![]()
![]()




A![]()
Тема 8. Параллельные прямая и плоскость общего положения
на чертеже
Упражнение 8.1
Решение

 a
a![]() || M
|| M![]() N
N![]() M
M![]()




 f
f![]()


 A
A![]() N
N![]()






 f
f![]() A
A![]() M
M![]() M
M![]() N
N![]() || a
|| a![]()
a![]() N
N![]()
Упражнение 8.2
Решение



 B
B![]() f
f![]() ||
A
||
A![]() B
B![]()
A![]() M
M![]() C
C![]()







C![]()


 M
M![]()
 f
f![]()


 A
A![]() B
B![]()
Упражнение 8.3
Решение
a![]() ||
p
||
p![]() a
a![]() ||
p
||
p![]()






 B
B![]() B
B![]() p
p![]()
p![]()
 A
A![]() A
A![]()



Упражнение 8.4
Решение


 f
f![]() f
f![]()




 A
A![]() A
A![]()

 f
f![]() ||
f
||
f![]()





M![]() M
M![]()
f![]()





B![]() B
B![]()


C![]() C
C![]()

Упражнение 8.5
Решение






 A
A![]() B
B![]()
![]()





 m
m![]() ||
||
![]()

 a
a![]() ||
||![]() C
C![]() M
M![]()






 C
C![]() B
B![]() m
m![]() ||
a
||
a![]()
a![]() M
M![]()
A![]()
Упражнение 8.6
Решение



 a
a![]() ||
n
||
n![]() b
b![]() ||
m
||
m![]()


 m
m![]() A
A![]() n
n![]()




m![]() A
A![]() n
n![]()
a![]() ||
n
||
n![]() b
b![]() ||
m
||
m![]()
Упражнение 8.7
Решение


 b
b![]() ||
m
||
m![]() a
a![]() A
A![]()



h![]() m
m![]()







 h
h![]() a
a![]() A
A![]()



b![]() m
m![]() ||
b
||
b![]()
Упражнение 8.8
Решение

 n
n![]() a
a![]() b
b![]()




 m
m![]() ||
n
||
n![]()



A![]()




 A
A![]()
b![]()


 a
a![]()
n![]() =
m
=
m![]()
Тема 9. Параллельные плоскости общего положения на чертеже
Упражнение 9.1
Решение








 a
a![]() ||F
||F![]() E
E![]() B
B![]() F
F![]()


D![]() b
b![]() ||A
||A![]() B
B![]()







 A
A![]() C
C![]() E
E![]()




 C
C![]() E
E![]()

 A
A![]()


 b
b![]() ||A
||A![]() B
B![]()


 a
a![]() ||F
||F![]() E
E![]() B
B![]() D
D![]() F
F![]()
