2. Каноническая форма представления ограничений. Допустимые базисные решения.

Для решения задачи линейного программирования симплекс-методом применяется специальный аппарат формальных преобразований математической модели. Рассмотрим некоторые его положения. Пусть задана основная задача линейного программирования (см. (0.1) и (0.2)). Введя в левую часть каждого неравенства добавочную переменную, преобразуем его в уравнение и перейдём к другой, стандартной форме записи:

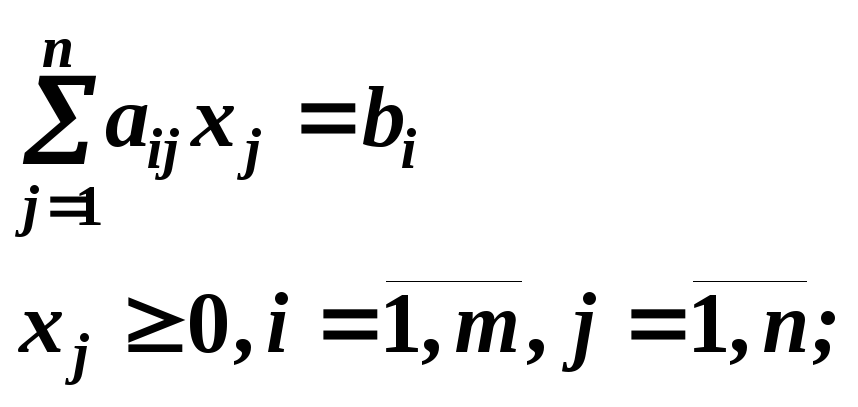(2.1)

(2.2)

При этом значения b_i должны быть неотрицательными. В случаеb_i < 0 обе части уравнения умножают на ”- 1”. Заметим, что при максимизацииzзадача сводится к стандартной путём замены: maxz = - min (-z) .

Систему (2.1) после несложных преобразований можно привести к виду:

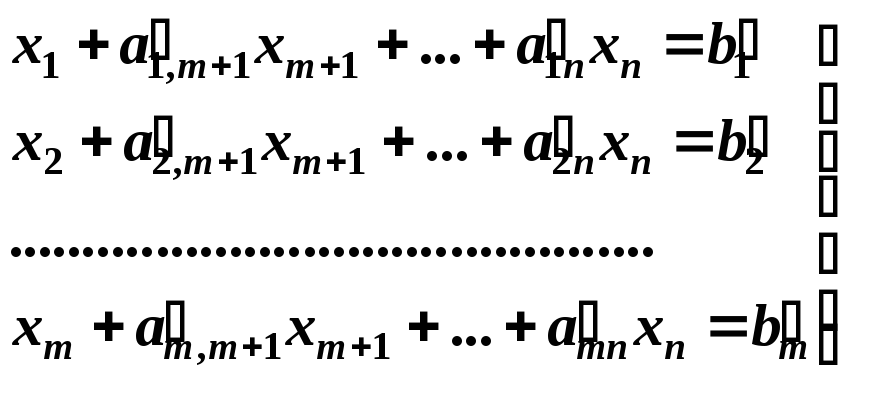(2.3)

Здесь b_i  0. Коэффициенты при переменныхравны единице (+1). Данная система представлена в канонической форме записи. Если количество переменных превышает количество уравнений, то существует бесчисленное множество решений системы.

Пусть m < n . Разделим все переменные системы (2.3) на две части:

а) основные переменные, количество которых должно быть равно количеству линейно-независимых переменных (m);

б) неосновные переменные, количество которых будет равно n – m .

Назначим первые m переменных (x₁ , x₂ , … ,x_m) в качестве основных. Тогда систему (2.3) можно решить относительноx₁ , x₂ , … ,x_m, если определитель m-го порядка, составленный из коэффициентов при переменныхx₁ , x₂ , … ,x_m не равен нулю (Д0) .

Придавая неосновным (независимым) переменным произвольные числовые значения, получим некоторое решение данной системы, причём каждому набору значений независимых переменных будет соответствовать одно определённое решение системы.

Основные (зависимые, несвободные) переменные будем называть базисными, неосновные (независимые, свободные) – небазисными переменными.

Можно составить бесчисленное множество различных наборов значений независимых переменных. Из всех этих решений в линейном программировании нас будет интересовать так называемые допустимые базисные решения.

Допустимое базисное решение системы линейных уравнений при m < n – это такое решение, в котором неосновным (независимым, небазисным) переменным даны нулевые значения, а значения базисных переменных являются неотрицательными (решение на грани или вершине симплекса, см. рис.1.2.а) и б)).

В теории линейного программирования доказывается, что если оптимальное решение задачи существует, то оно совпадает по крайней мере с одним из допустимых базисных решений.

Поиск и направленные переходы от одних допустимых базисных решений к другим с целью определения оптимального решения может быть выполнен численным методом. Один из них рассмотрим ниже.

3.Симплекс-метод. Анализ процедуры решения задачи линейного программирования (с примером).

Рассмотрим вычислительные и логические процедуры, обеспечивающие поиск решения задачи линейного программирования симплекс-методом. Процедуры поясняются в процессе решения конкретной задачи: найти совокупность значений , удовлетворяющих системе неравенств:

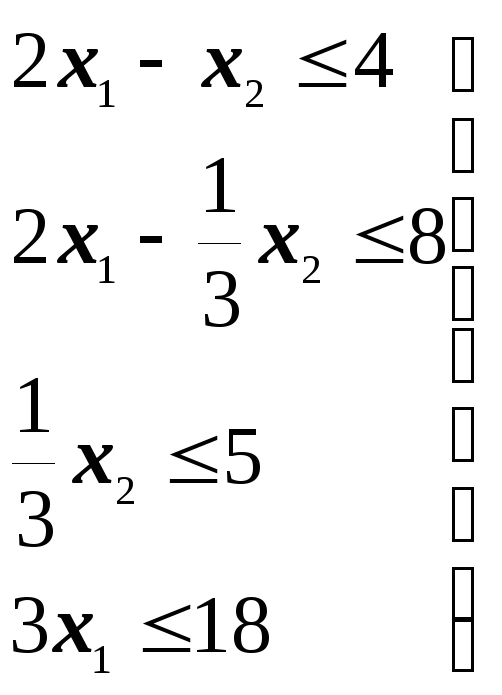(3.1)

и условиям неотрицательности переменных , для которых

целевая функция

z=10+7x₁-5/3x₂(3.2)

достигает максимума.

Преобразуем заданную форму задачи в каноническую, введя дополнительные переменные . Получим систему линейных уравнений (здесь дополнительные переменные составляют единичный базис):

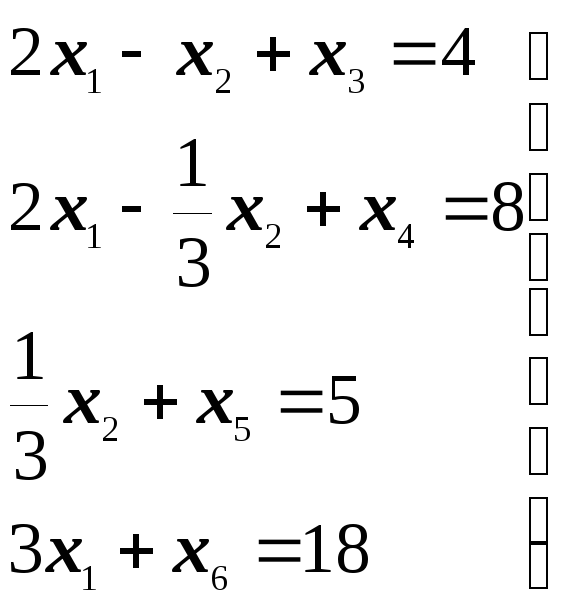(3.3)

и форму z:(3.4)

Выберем в качестве свободных (независимых) переменных и, так как через них выражена линейная форма; переменные,,,- базисные. Так как все величиныдолжны быть неотрицательны, то их наименьшие значения равны нулю:,. Подставив эти значения в систему, получим следующие значения несвободных (базисных) переменных:. Эти значения также положительны, поэтому система значений;;образует допустимое базисное решение системы (3.3). При найденном решении значениеzоказывается равным «-10».

Выше были приняты значения свободных переменных равными нулю (наименьшими при условии их неотрицательности). Попробуем за счёт их увеличения добиться уменьшения формы z .

Из выражения целевой функции видно, что, так как входит в неё со знаком плюс, то её увеличение может привести только к увеличению значенияz. Неизвестнаявходит в неё со знаком минус, поэтому её увеличение «выгодно». Однако неограниченное увеличение этой свободной неизвестной может привести к отрицательности несвободных (базисных) неизвестных, то есть привести к недопустимому решению. Так, из первого уравнения видно, что, еслистанет больше двух (остаётся свободной и равной нулю), тостанет отрицательной. Таким образом, при,остальные переменные примут значения:, следовательно, получаем новое допустимое базисное решение. Теперь свободными сталии; остальные – базисными. Проведя преобразования (выразив ограничения и линейную форму через новые свободные переменные) получим:

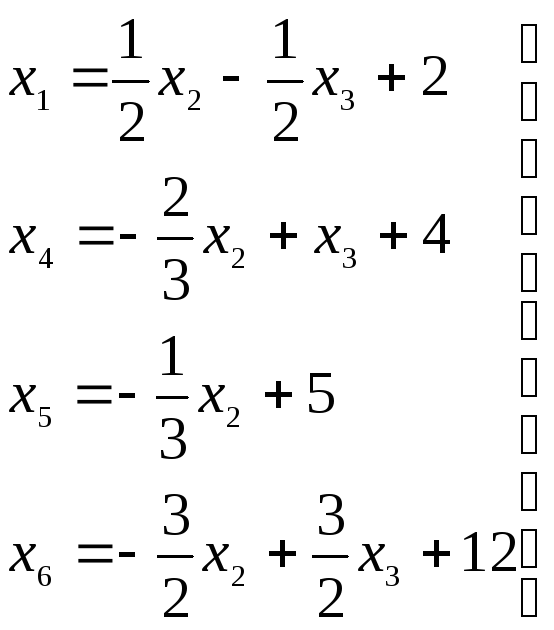(3.5)

(3.6)

Соответствующее допустимое базисное решение:

;;

Проведя аналогичные рассуждения, принимая во внимание, что входит в целевую функцию со знаком минус, на основе второго уравнения из системы (3.5) увеличиваемдо значения= 6. При этом происходит ввод переменнойв базис и вывод из негов качестве свободной. Получаем:

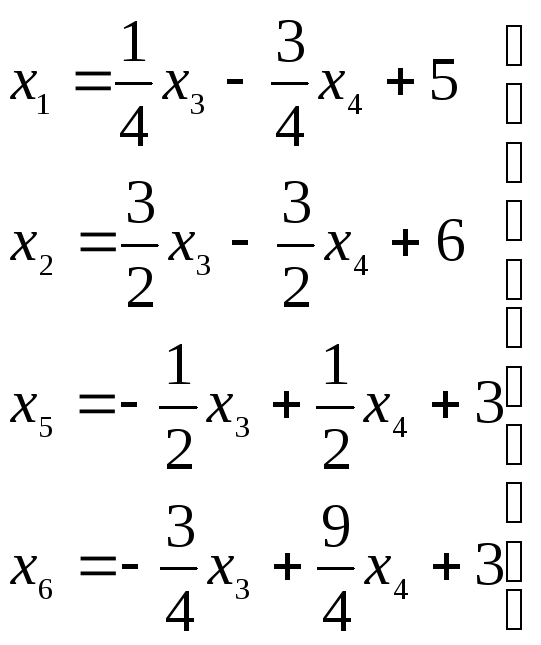(3.7)

(3.8)

Теперь свободные неизвестные входят в выражение линейной формы со знаком плюс. Их увеличение может привести только к увеличению формы. Следовательно, базисное решение, являющееся оптимальным, имеет вид:

;;,

минимальное значение формы: , а максимальное значение.

Таким образом, идея симплекс-метода преобразования модели заключается в таком итеративном направленном переходе от одного допустимого базисного решения к другому, при котором последовательно улучшается значение линейной формы.