11 Класс

1. (10 баллов) В открытой прямоугольной коробке сидит кузнечик, который умеет прыгать со скоростьюм/с под любым углом к горизонту. На какой минимальный угол нужно наклонить коробку, чтобы кузнечик мог из нее выпрыгнуть? Считать, что каждая грань коробки является квадратом со сторонойсм. Ускорение свободного падениям/с². Сопротивлением воздуха пренебречь.

Решение: Выберем координатные оси X и Y, как показано на рисунке. Тогда в момент преодоления кузнечиком края коробки проекция его скорости на осьY должна быть равна нулю, а координата , и можно записать следующие соотношения:

,

,

где и- проекция векторов ускорения и начальной скорости кузнечика на осьY. Отсюда . При фиксированных значениях углаи начальной скоростимаксимальная высота над дном коробки достигается при, то есть кузнечику следует прыгать перпендикулярно дну коробки. При этом

, .

Вдоль оси X за время сместиться на расстояние, где. Отсюдасм. Таким образом, размеры дна коробки достаточно велики, чтобы кузнечик мог стартовать на нужном удалении от стенок.

1. Правильный выбор системы координат – 1 балл.

2. Найдена максимальная высота – 1 балл.

3. Сделан вывод о том, что скорость должна быть направлена перпендикулярно дну коробки – 2 балла.

4. Получено выражение для угла – 2 балла

5. Определено значение угла – 2 балла.

6. Проведена оценка размеров коробки – 2 балла.

2. (10 баллов) Тележка с водой движется по горизонтальной поверхности с постоянным ускорением. На тележку под угломк вертикали падает луч света, который после отражения распространяется под угломк вертикали (направления ускорения тележки и лучей показаны на рисунке). Найдите ускорениетележки. Ускорение свободного падения.

Решение. Из закона отражения света вытекает, что нормаль к свободной поверхности воды направлена под углом к вертикали.

Следовательно, свободная поверхность воды наклонена под этим углом к вертикали. Рассмотрим слой воды массой на свободной поверхности. Запишем для него второй закон Ньютона в проекции на плоскость, касательную к этой поверхности:

.

отсюда

.

1. Выполнен рисунок – 3 балла.

2. Применен закон отражения и получено выражение для угла между нормалью и вертикалью – 2 балла.

3. Записан второй закон Ньютона – 3 балла.

4. Получено выражение для ускорения – 2 балла.

3. (10 баллов) Цикл тепловой машины состоит из двух изобар и двух изотерм, при этом работа при изобарическом расширении такая же, как и при изотермическом. Найдите КПД такого цикла, если рабочим веществом является гелий, а максимальная температура в процессе вдвое больше минимальной.

Р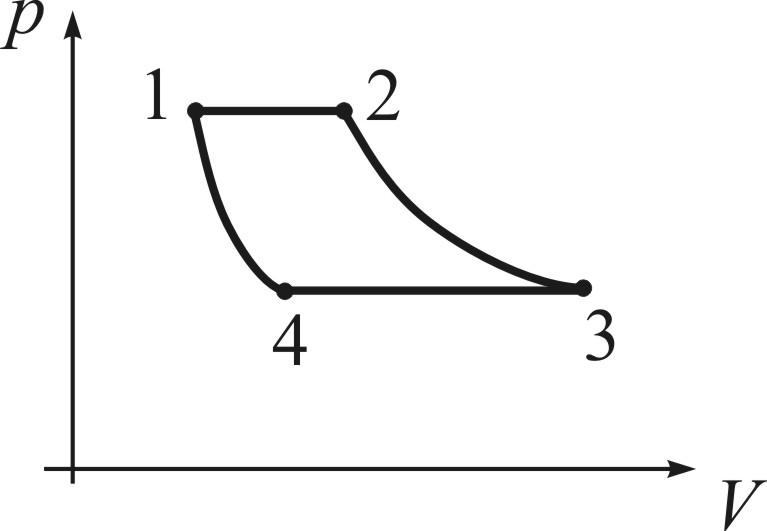ешение. Цикл представлен на pV-диаграмме: 1-2 и 3-4 – изобары, 2-3 и 4-1 – изотермы. КПД цикла равен отношению совершенной в цикле работы к полученному на участке 1-2-3 количеству теплоты.

Рассчитаем работу на различных участках цикла. Обозначим работу на участке 1-2 через ; тогда для работы на участке имеем. Для расчета работы на участке 3-4 учтем, что в силу условия задачи,,,,. Поэтому,,; отсюда

.

Для расчета работы на участке 4-1 заметим, что кривая 1-4 получается из кривой 2-3 сжатием в два раза вдоль оси , поэтому площади под кривыми 1-4 и 2-3 отличаются в два раза:. Суммарная работа в цикле, таким образом, равна

.

Рассчитаем полученные газом количества теплоты на участках 1-2 и 2-3. Сообщаемое газу количество теплоты идет на изменение его внутренней энергии, которая для одноатомного гелия равна , и на совершение работы:,. Суммарное количество теплоты, полученное на участке 1-2-3, равно.

Следовательно, КПД цикла равен .

1. Представлена pV-диаграмма цикла – 1 балл.

2. Получены выражения ,,- 2 балла.

3. Определена работа на участке 3-4 – 2 балла.

4. Определено значение работы на участке 1-4 – 2 балла.

5. Определено количество теплоты в процессе – 2 балла.

6. Найдено КПД цикла – 1 балл.

4. (10 баллов) Резисторы, сопротивлениямиОм,Ом,иОм припаяны к клеммамA, B, C, D и E так, как показано на рисунке. Имеется источник тока с ЭДС В и внутренним сопротивлениемОм, а также много соединительных проводов малого сопротивления, которые можно подключать к источнику и к любой из клемм. Как нужно соединить источник и резисторы, чтобы общая тепловая мощность, выделяющаяся на резисторах, была максимальной? Чему равна эта мощность?

Решение. Искомая тепловая мощность максимальна, когда сопротивление нагрузки равно внутреннему сопротивлению источникаОм. Это достигается с наибольшей точностью при параллельном соединении всех резисторов, так что их общее сопротивлениеОмОм, аВт.

1. Определено условие максимума мощности – 1 балл.

2. Показано, что проводники должны быть соединены параллельно – 2 балла.

3. Представлено соединение проводников – 4 балла.

4. Найдена максимальная мощность – 3 балла.

5. (10 баллов) Участок гибкого провода массойподвешен так, что его концы закреплены на одинаковой высоте. Провод находится в однородном горизонтальном магнитном поле с индукцией, и по нему течет ток. Силы, действующие на провод в точках подвеса, образуют уголс горизонтом. Найдите силунатяжения провода в нижней его точке. Размерыиизвестны.

Решение. Обозначим нижнюю точку провода через , верхние точки – черези. Введем в плоскости провода систему координат, направив осьвправо, ось– вверх; обозначим координаты точекикаки.

Рассмотрим участок провода . На него действуют: направленная вниз сила тяжести, направленная влево силанатяжения нити в нижней точке, направленная под угломк горизонту сила натяжения нитии сила Ампера. Запишем условия равновесия системы в проекциях на осии:

.

Выражая из второго соотношения неизвестную величину и подставляя ее в первое уравнение, находим искомую силу натяжения нити:

.

Для получения ответа остается найти компоненты силы Ампера . Рассмотрим маленький отрезок провода длиной, составляющий уголс горизонтом и расположенный между точками с координатамии, где,. На этот участок действует сила Ампера, равная по модулюи направленная под угломк вертикали.

Эта сила имеет компоненты:

,

.

Складывая силы Ампера, действующие на все малые отрезки участка АС провода, находим:

,

.

Подставляя результат в формулу для силы натяжения провода, приходим к ответу:

.

1. Определены силы, действующие на элемент провода – 2 балла.

2. Записано условие равновесия – 1 балл.

3. Найдены составляющие сила Ампера – 4 балла.

4. Получено выражение для силы натяжения – 3 балла.