
9 Класс
1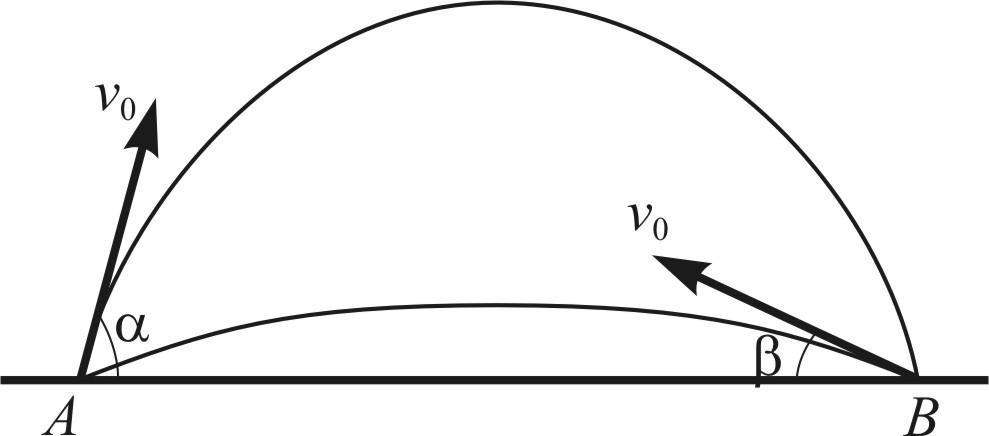 .
(10 баллов) Из точекА
и В,
находящихся на одной горизонтальной
прямой, одновременно бросили два камня
с одинаковыми по модулю скоростями
.
(10 баллов) Из точекА
и В,
находящихся на одной горизонтальной
прямой, одновременно бросили два камня
с одинаковыми по модулю скоростями
![]() м/с. Один из них полетел по навесной
траектории, а другой по настильной и
каждый упал в точку старта другого
камня. Известно, что угол бросания камня
из точки
м/с. Один из них полетел по навесной
траектории, а другой по настильной и
каждый упал в точку старта другого
камня. Известно, что угол бросания камня
из точки![]() составляет 75о.
Определите скорость одного камня
относительно другого.
составляет 75о.
Определите скорость одного камня
относительно другого.
Решение. Рассмотрим полет камня брошенного из точки А:
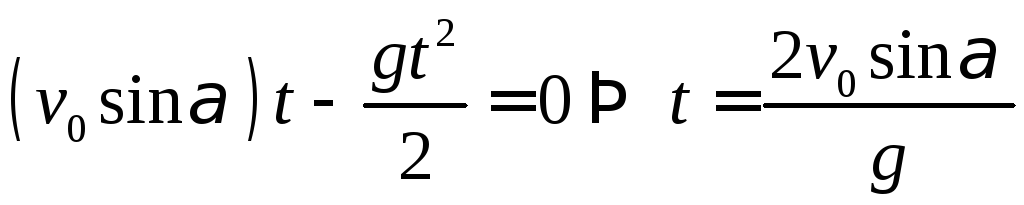 ,
,
Расстояние между точками А и В равно:
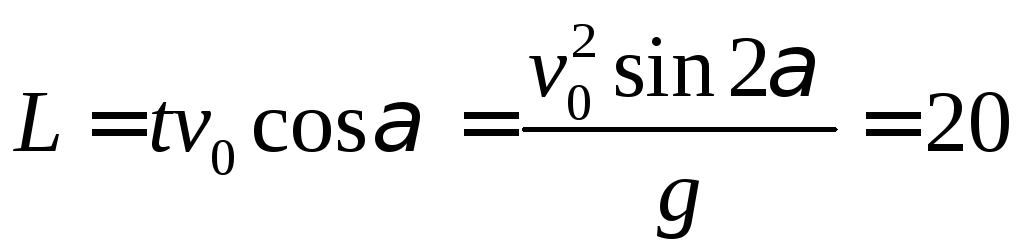 м.
м.
Поскольку для камня, брошенного из точки В, можно аналогичным образом записать
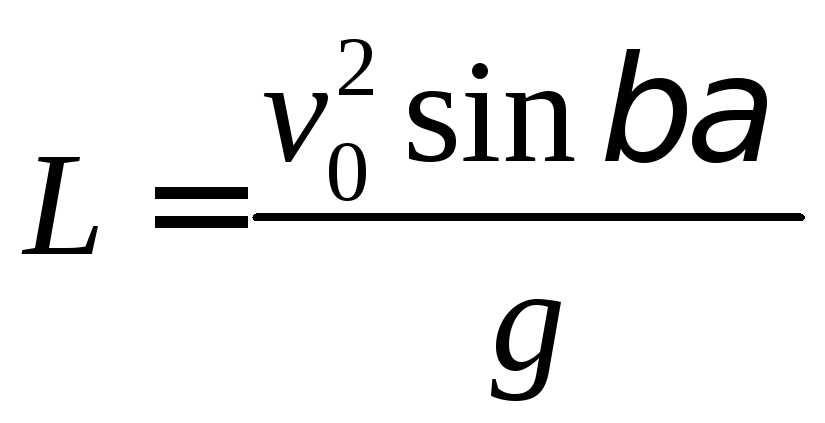 ,
,
мы получим,
![]() ,
а поскольку
,
а поскольку![]() по условию задачи, то
по условию задачи, то![]() ,
то есть
,
то есть![]() .
.
Так как
![]() ,
и
,
и![]() ,
то вектор
,
то вектор![]() есть диагональ квадрата, построенного
на векторах
есть диагональ квадрата, построенного
на векторах![]() и
и![]() .
Поэтому
.
Поэтому![]() м/с.
м/с.
Получено условие
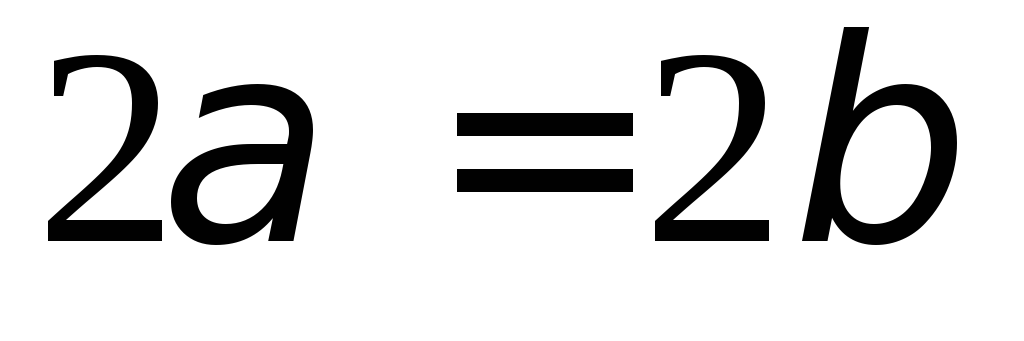 – 2 балл.
– 2 балл.Показано, что
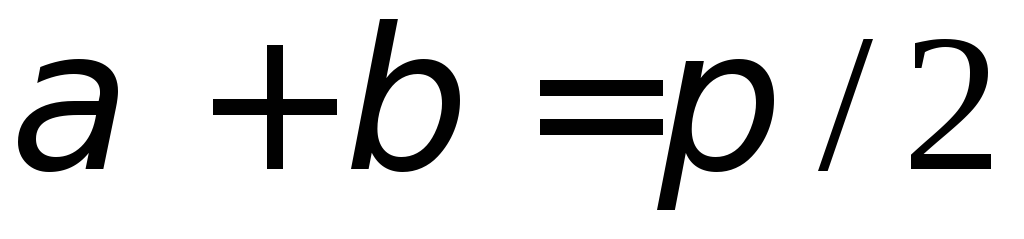 и
и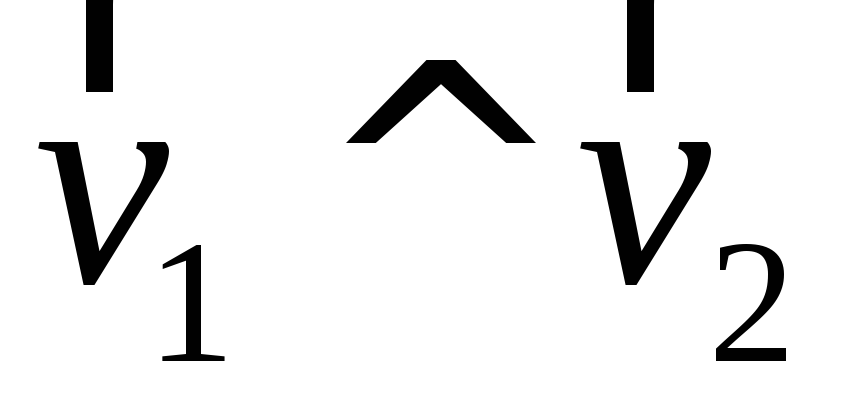 – 3 балла.
– 3 балла.Сделан вывод о том, что вектор относительной скорости – диагональ – 3 балла.
Получен ответ – 2 балла.
2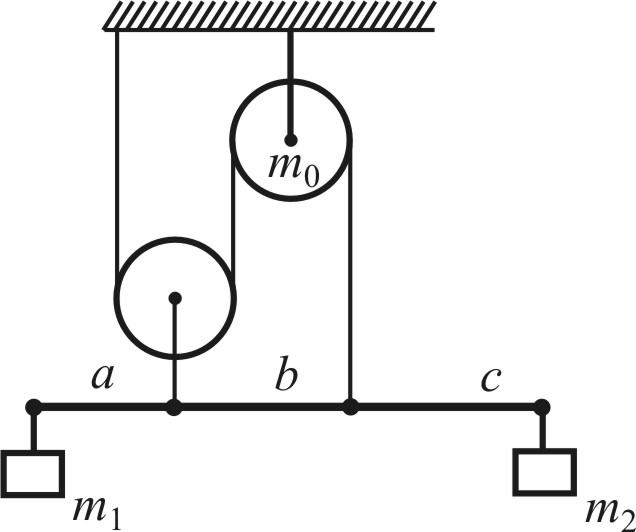 .
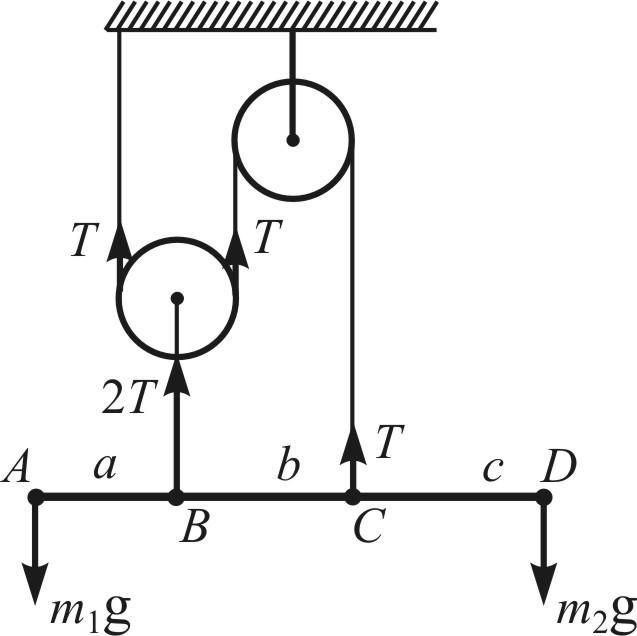
(10 баллов) Рычаг подвешен к системе
блоков так, что точки подвеса делят его
в отношении
.
(10 баллов) Рычаг подвешен к системе
блоков так, что точки подвеса делят его
в отношении![]() .
Блоки, рычаг и нити невесомы, трения
нет. Каково отношение масс грузов
.
Блоки, рычаг и нити невесомы, трения
нет. Каково отношение масс грузов![]() и
и![]() ,
если система находится в равновесии?
,
если система находится в равновесии?
Решение.
Пусть перекинутая через блоки нить
натянута с силой
![]() .
Тогда к рычагу приложены следующие
силы: в точке А – направленная вниз сила
.
Тогда к рычагу приложены следующие
силы: в точке А – направленная вниз сила![]() ,
в точке В – направленная вверх сила
натяжения нити
,
в точке В – направленная вверх сила
натяжения нити![]() ,
в точке С – направленная вверх сила
натяжения нити
,
в точке С – направленная вверх сила
натяжения нити![]() ,
в точке
,
в точке![]() - направленная вниз сила тяжести
- направленная вниз сила тяжести![]() .
Поскольку геометрическая сумма сил,
действующих на рычаг, должна быть равна
нулю, получаем первое уравнение:
.
Поскольку геометрическая сумма сил,
действующих на рычаг, должна быть равна
нулю, получаем первое уравнение:
![]() ,
,
из которого находим,
![]() .
.
Запишем правило равновесия рычага относительно одной из точек, например, относительно точки А:
![]()
 .
.
Подставляя в это
отношение значение
![]() ,
находим
,
находим
![]() .
.
Отсюда
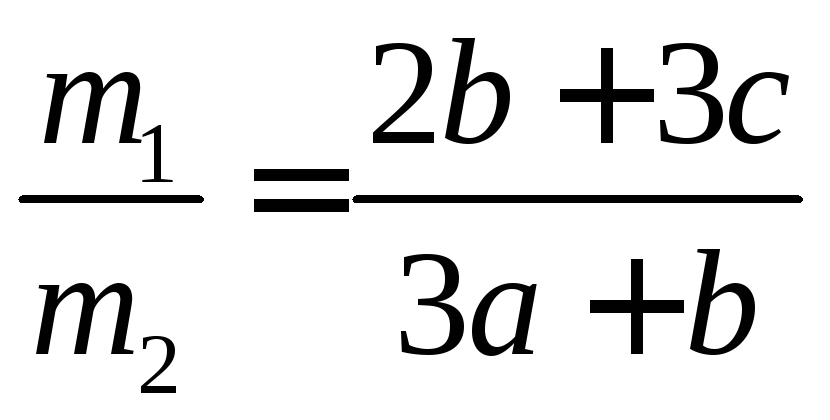 .
.
1. Нарисован рисунок с изображением всех сил – 2 балла.
2. Записано условие равенства нулю суммы всех сил – 2 балла.
3. Записано условие равенства нулю моментов сил – 3 балла.
4. Решена система уравнений и получен ответ – 3 балла.
3. (10 баллов) В
палатке, покрытой сверху шерстяными
одеялами, пол застелен теплонепроницаемым
войлоком. Одинокий спящий индеец начинает
мерзнуть в палатке при уличной температуре
воздуха
![]() .
Два спящих индейца начинают мерзнуть
в этой палатке при уличной температуре
воздуха
.
Два спящих индейца начинают мерзнуть
в этой палатке при уличной температуре
воздуха![]() .
При какой температуре воздуха
.
При какой температуре воздуха![]() индейцы начинают пользоваться палатками?
При какой температуре воздуха
индейцы начинают пользоваться палатками?
При какой температуре воздуха![]() в той же палатке станет холодно терм
индейцам? Считайте, что количество
теплоты, теряемой палаткой в единицу
времени, пропорционально разности
температур воздуха внутри и снаружи.
в той же палатке станет холодно терм
индейцам? Считайте, что количество
теплоты, теряемой палаткой в единицу
времени, пропорционально разности
температур воздуха внутри и снаружи.
Решение: Индейцы
начинают пользоваться палатками, когда
начинают мерзнуть на улице, то есть при
температуре воздуха
![]() .
Индейцам станет холодно в палатке, когда
температура в ней опуститься ниже
.
Индейцам станет холодно в палатке, когда
температура в ней опуститься ниже![]() .
.
Пусть
![]() - тепловая «мощность» одного индейца,
- тепловая «мощность» одного индейца,![]() - температура уличного воздуха, при
которой в палатке станет холодно
- температура уличного воздуха, при
которой в палатке станет холодно![]() индейцам, тогда уравнение теплового
баланса для палатки имеет вид
индейцам, тогда уравнение теплового
баланса для палатки имеет вид
![]() ,
,
Где
![]() - коэффициент, который зависит только
от свойств палатки. Слева в уравнении
стоит суммарная тепловая мощность, а
справа – мощность теплоотдачи в
окружающую среду. Запишем это уравнение
конкретно для каждого случая:
- коэффициент, который зависит только
от свойств палатки. Слева в уравнении
стоит суммарная тепловая мощность, а
справа – мощность теплоотдачи в
окружающую среду. Запишем это уравнение
конкретно для каждого случая:
![]() ,
,
![]() ,
,
![]() .
.
Решая систему, находим,
![]()
![]() .
.
Записано уравнение теплового баланса в общем виде – 2 балла.
Записана система уравнений для каждого случая – 2 балла.
Найдена температура
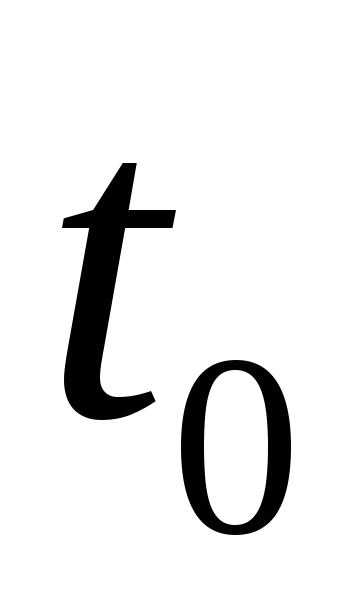 - 3 балла.
- 3 балла.Найдена температура
 - 3 балла.
- 3 балла.
4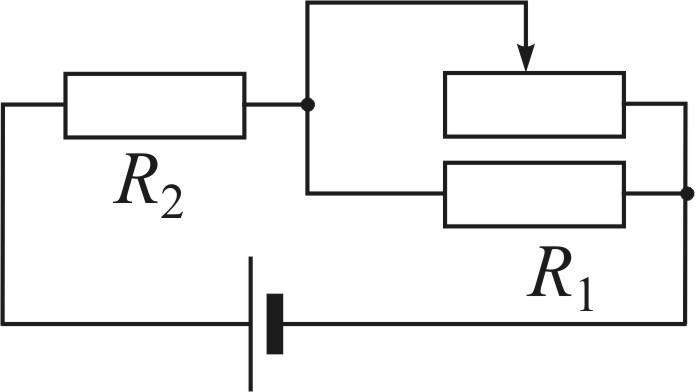 .
(10 баллов) К источнику постоянного тока
с напряжением 4 В подключены согласно
схеме два одинаковых резистора по 10 Ом
каждый и реостат, сопротивление которого
можно менять от 0 до 5 Ом. При каком
положении ползунка реостата мощность,
выделяемая на резисторе
.
(10 баллов) К источнику постоянного тока
с напряжением 4 В подключены согласно
схеме два одинаковых резистора по 10 Ом
каждый и реостат, сопротивление которого
можно менять от 0 до 5 Ом. При каком
положении ползунка реостата мощность,
выделяемая на резисторе![]() максимальна? Каково ее значение? Какая
мощность выделяется в этом случае на
резисторе
максимальна? Каково ее значение? Какая
мощность выделяется в этом случае на
резисторе![]() ?
?
Решение.
Пусть
![]() - сопротивление реостата. Общее
сопротивление параллельного участка
- сопротивление реостата. Общее
сопротивление параллельного участка
![]() ,
,
напряжение на этом участке
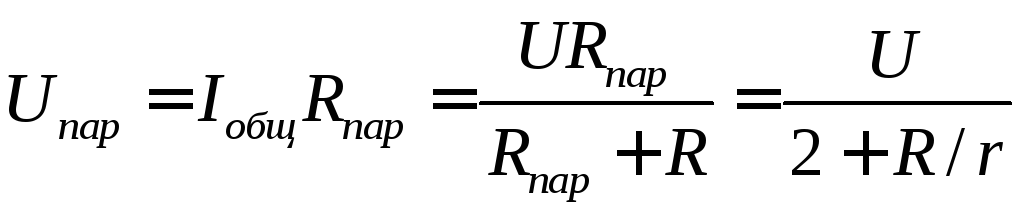 .
.
Мощность, выделяемая
на резисторе
![]() :
:
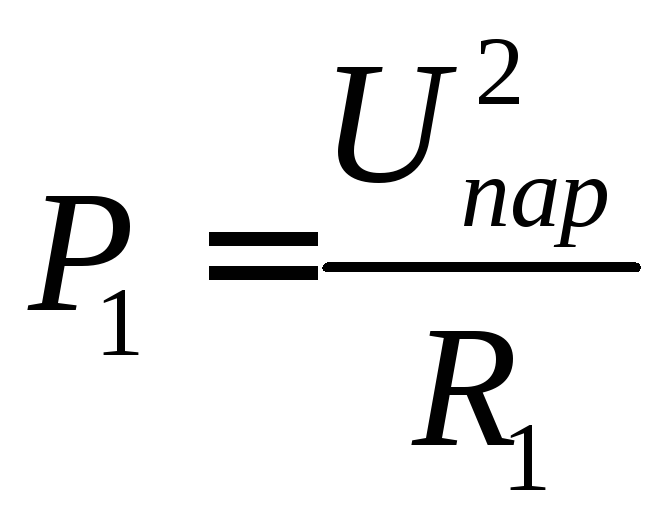 ,
,
чем больше
![]() ,
тем больше
,
тем больше![]() ,
следовательно, максимум
,
следовательно, максимум![]() достигается при
достигается при![]() Ом (крайнее левое положение).
Ом (крайнее левое положение).
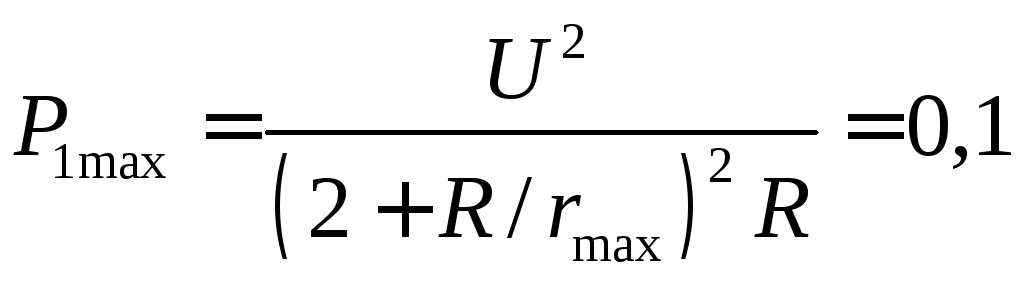 Вт.
Вт.
На втором резисторе
при этом
![]() :
:
![]() Вт,
Вт,
где
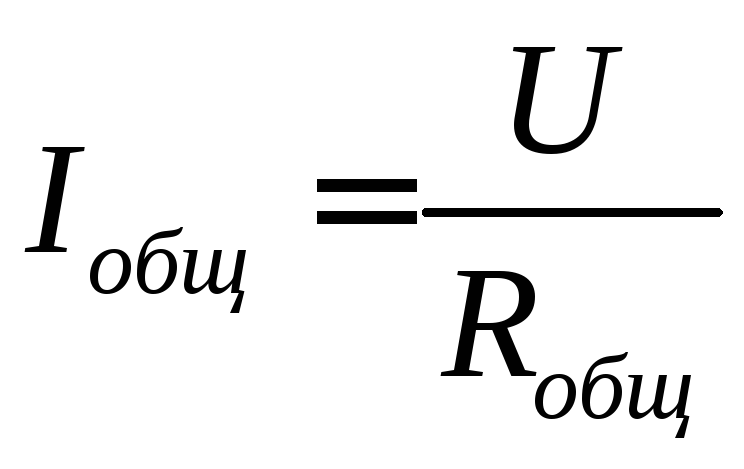 ,
,![]() ,
,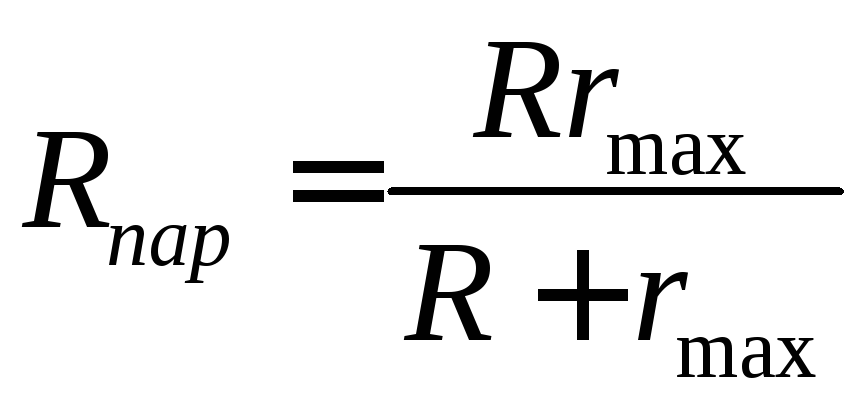 .
.
Найдено сопротивление параллельного участка – 1 балл.
Найдено напряжение на параллельном участке – 1 балл.
Найдена мощность, выделяемая на первом сопротивлении – 2 балла.
Сделан вывод о том, что максимальное значение мощности достигается при максимальном значении сопротивления реостата – 2 балла.
Найдено значение мощности, выделяемой на первом сопротивлении – 2 балла.
Найдено значение мощности, выделяемой на втором сопротивлении – 2 балла.
