11 Класс

1. (10 баллов) В открытой прямоугольной коробке сидит кузнечик, который умеет прыгать со скоростьюм/с под любым углом к горизонту. На какой минимальный угол нужно наклонить коробку, чтобы кузнечик мог из нее выпрыгнуть? Считать, что каждая грань коробки является квадратом со сторонойсм. Ускорение свободного падениям/с². Сопротивлением воздуха пренебречь.

2. (10 баллов) Тележка с водой движется по горизонтальной поверхности с постоянным ускорением. На тележку под угломк вертикали падает луч света, который после отражения распространяется под угломк вертикали (направления ускорения тележки и лучей показаны на рисунке). Найдите ускорениетележки. Ускорение свободного падения.

3. (10 баллов) Цикл тепловой машины состоит из двух изобар и двух изотерм, при этом работа при изобарическом расширении такая же, как и при изотермическом. Найдите КПД такого цикла, если рабочим веществом является гелий, а максимальная температура в процессе вдвое больше минимальной.

4. (10 баллов) Резисторы, сопротивлениямиОм,Ом,иОм припаяны к клеммамA, B, C, D и E так, как показано на рисунке. Имеется источник тока с ЭДС В и внутренним сопротивлениемОм, а также много соединительных проводов малого сопротивления, которые можно подключать к источнику и к любой из клемм. Как нужно соединить источник и резисторы, чтобы общая тепловая мощность, выделяющаяся на резисторах, была максимальной? Чему равна эта мощность?

5. (10 баллов) Участок гибкого провода массойподвешен так, что его концы закреплены на одинаковой высоте. Провод находится в однородном горизонтальном магнитном поле с индукцией, и по нему течет ток. Силы, действующие на провод в точках подвеса, образуют уголс горизонтом. Найдите силунатяжения провода в нижней его точке. Размерыиизвестны.

Муниципальный этап

Всероссийской олимпиады школьников по физике

2009-2010 Учебный год

8 Класс

1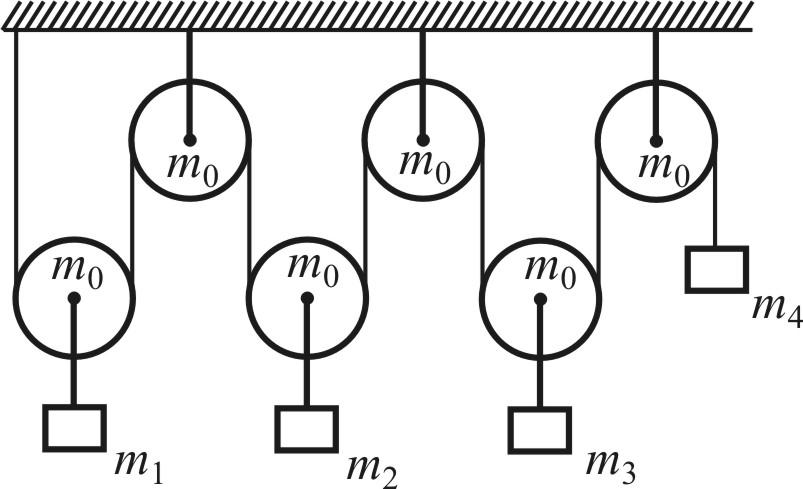. (10 баллов) В системе, изображенной на рисунке, масса самого правого груза равнакг, а массы всех блоков одинаковы и равныг. Система уравновешена и неподвижна. Найдите массы грузов,и. Массой троса и трением в блоках пренебречь.

Решение:

Поскольку система находится в равновесии, то сумма всех сил, действующих на каждый блок должна равняться нулю, откуда следует

.

Из первого уравнения находим:

Н.

Подставляя это значение во второе уравнение:

кг.

1. Нарисован рисунок с изображением всех сил – 3 балла.

2. Записаны условия равновесия – 2 балла.

3. Найдено значение силы натяжения нити Т – 2 балла.

4. Решена система уравнений и получен ответ – 3 балла.

2. (10 баллов) Кусок льда, внутри которого вморожен шарик из свинца, плавает в цилиндрическом сосуде с водой. Площадь дна сосуда . Какова масса шарика, если после полного таяния льда уровень воды в сосуде понизился на. Плотность свинца, плотность воды.

Решение. Пусть начальный уровень воды в сосуде равен . Тогда сила давления воды на дно сосуда будет равной

.

После таяния льда вес содержимого сосуда не изменится. Поэтому и сила давления на дно сосуда не изменится. Однако при этом сила равна сумме сил давления столба воды высотой:

,

равнодействующей силы тяжести шарика

и архимедовой силы

,

где имасса и объем шарика.

Таким образом:

.

Отсюда

1. Определена сила давления воды со льдом на дно сосуда – 1 балл.

2. Сформулировано условие того, что после таяния льда давление на дно сосуда не изменится – 2 балла.

3. Определено суммарная сила давление на дно сосуда после таяния льда – 2 балла.

4. Записано условие равенства сила давления до и после таяния льда – 3 балла.

5. Получен конечный ответ – 2 балла.

3. (10 баллов) Три одинаковых сообщающихся сосуда частично заполнены водой. Когда в левый сосуд налили слой керосинасм, а в правый высотойсм, то уровень воды в среднем сосуде повысился. На сколько повысился уровень воды в соседнем сосуде? Плотность керосинаг/см³, плотность воды г/см³.

Решение. Предположим, что в левом сосуде уровень воды понизился на , а в правом – на. Тогда в среднем сосуде уровень воды повысился наи будет выше, чем в правом наи выше чем в левом на. Так как жидкости находятся в равновесии, то давление столбов воды равно давлению столбов керосина:

,

,

или

,

.

Подставив значения, получим см,см. Откудасм.

1. Определена разность уровней воды в крайних сосудах – 3 балла.

2. Записано условие равенства гидростатических давлений – 4 балла.

3. Получен конечный ответ – 3 балла.

4. (10 баллов) Самолет летит по маршруту А-В-А. Скорость самолета в безветренную погоду равна . В каком случае самолету потребуется меньше времени на преодоление маршрута – в безветренную погоду или когда дует ветер вдоль линии? Чему равна средняя скорость во втором случае? Скорость ветра равна.

Решение. На пути скорость самолета равна, на путиравна. Время перелетаравно, время перелетаравно(- расстояние). Полное время полета в ветреную погоду

,

таким образом, с учетом того, что время полета в безветренную погоду , получаем

,

то есть в безветренную погоду на перелет потребуется меньше времени.

Средняя скорость

.

1. Найдены скорости полета в ветреную погоду – 1 балл.

2. Найдено полное время полета – 2 балла.

3. Сделан вывод об отношении времен полета – 3 балла.

4. Найдена средняя скорость – 4 балла.