Kursovaya_rabota_po_teplomassoobmenu_Marsa

─ 16 ─

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

МАГНИТОГОРСКИЙ ГОСУДАРСТВЕННЫЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Г.И.НОСОВА

КАФЕДРА ТЕПЛОТЕХНИЧЕСКИХ И ЭНЕРГЕТИЧЕСКИХ СИСТЕМ

КУРСОВАЯ РАБОТА

ПО ТЕПЛОМАССООБМЕНУ

Выполнил: студент гр. ЭТ-05-2

Насыров М.Ш.

Проверил: ст. преподаватель

д.т.н. Матвеева Г.Н.

Магнитогорск

2007

Задача 1. Нестационарная теплопроводность

Металлическая заготовка, имеющая форму пластины (циллиндра), неограниченной длинны, с начальной температурой , нагревается в печи, температура которой поддерживается постоянной до конечной температуры по оси заготовки . Считая длинну (и высоту) заготовки большими большими по сравнению с толщиной, определить:

1. Время нагревания заготовки до данной конечной температуры;

2. Температуры на оси и на поверхности заготовки для различных моментов времени (с использование монограмм Будрина);

3. Распределение температуры по толщине заготовки для четырёх моментов времени (с использованием аналитических формул);

4. Количество теплоты, подведённой к телу в течении всего периода нагревания (на 1 поверхности пластины или на 1 длинны циллиндра);

5. По результатам (2) и (3) построить графики.

1._Определение времени нагревания заготовки до конечной температуры

Сначала найдем из справочных таблиц теплофизические параметры цилиндра (теплоёмкость, коэффициент теплопроводности, коэффициент температуропроводности и плотность) при начальной температуре и конечной температуре центра цилиндра , и вычислим их средние значения:

Параметр			Среднее
	0,52	0,69	0,605
	45,12	29,42	37,27
	0,037	0,021	0,029
	7800	7436	7618

Вычислим число и безразмерную температуру для центра цилиндра в последний момент времени нагрева:

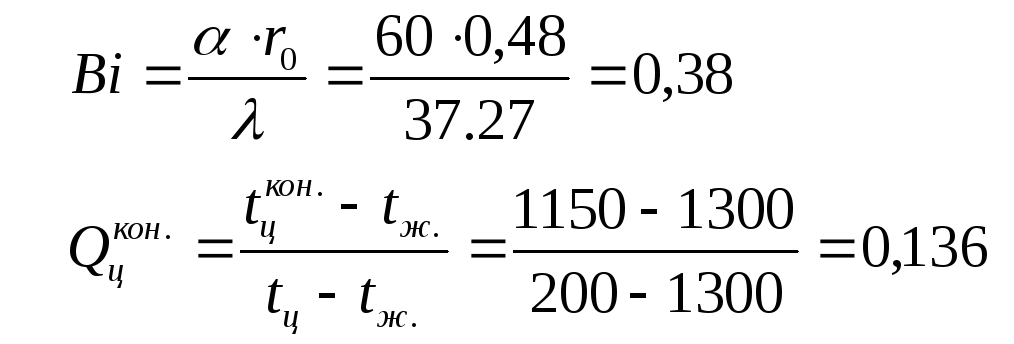
По номограмме Будрина для центра цилиндра определим:

Вычислим время нагревания заготовки:

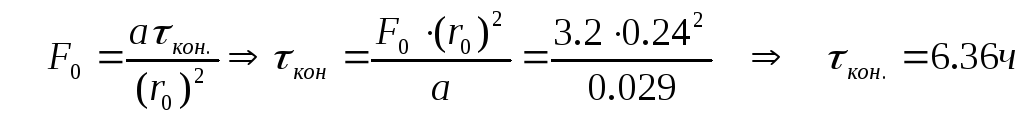
2._Определение температур на оси и на поверхности заготовки для различных моментов времени

Интервал времени нагревания заготовки разобьём на несколько промежутков. Для каждого значения вычислим время (в часах), найдём безразмерные температуры в центре и на поверхности цилиндра по номограммам Будрина (в зависимости от и ). По безразмерным температурам вычислим температуры в центре и на поверхности цилиндра в градусах Цельсия.

Для :

1. Время нагревания

2. Безразмерная температура в центре цилиндра (определяем по соответствующей диаграмме Будрина в зависимоси от 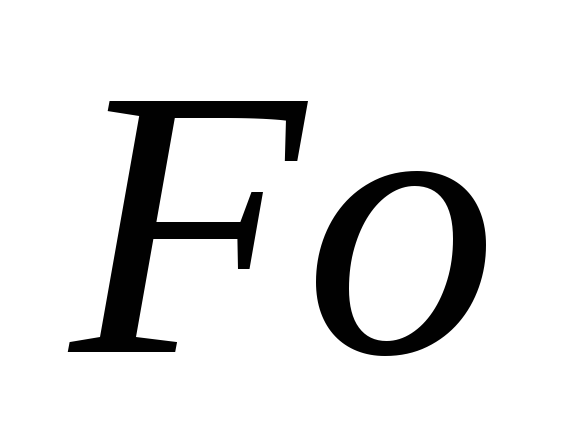и ):

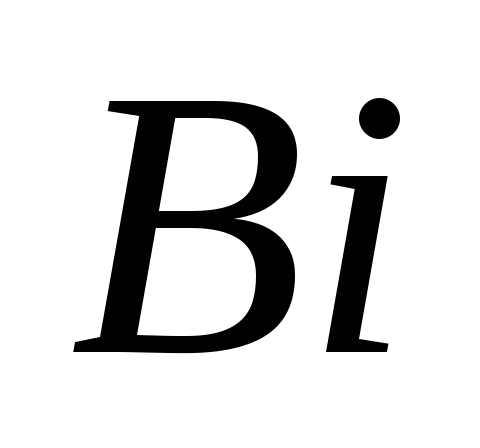3. Безразмерная температура на поверхности цилиндра (определяем по соответствующей диаграмме Будрина в зависимоси от 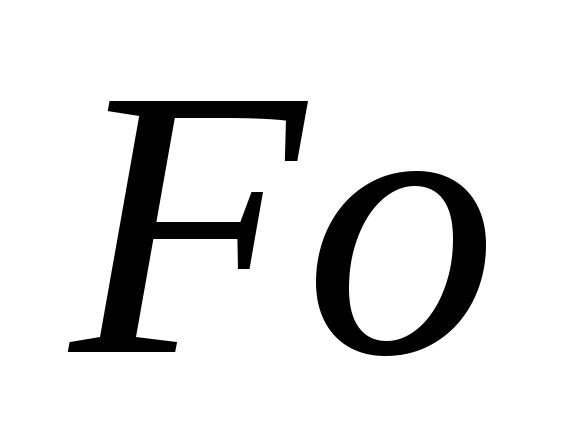и ):

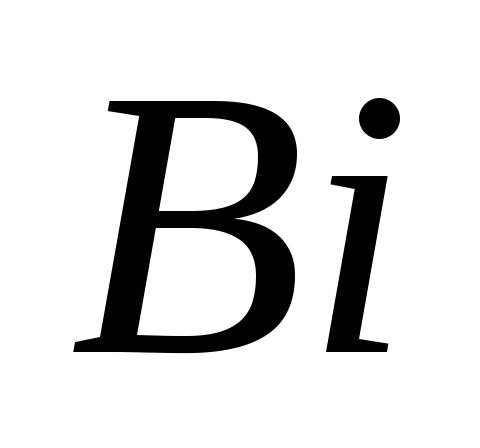4. Температура на оси циллиндра:

5. Температура на поверхности циллиндра:

Для остальных значений критерия Фурье вычисления производим по этим же формулам, результаты вычислений заносим в таблицу.

	0,4	0,8	1,2	1,6	2	2,4	2,8	3,2
	0,79	1,59	2,38	3,17	3,97	4,76	5,56	6,36
	0,79	0,58	0,46	0,36	0,27	0,21	0,16	0,136
	0,69	0,53	0,4	0,3	0,23	0,187	0,155	0,12
	431	662	794	904	1003	1069	1124	1150
	541	717	860	970	1047	1094,3	1129,5	1168

3._Определение распределения температуры по толщине заготовки для четырёх моментов времени

При определим из таблиц:

0,386	1.089	0.8375	0.7025	0,906

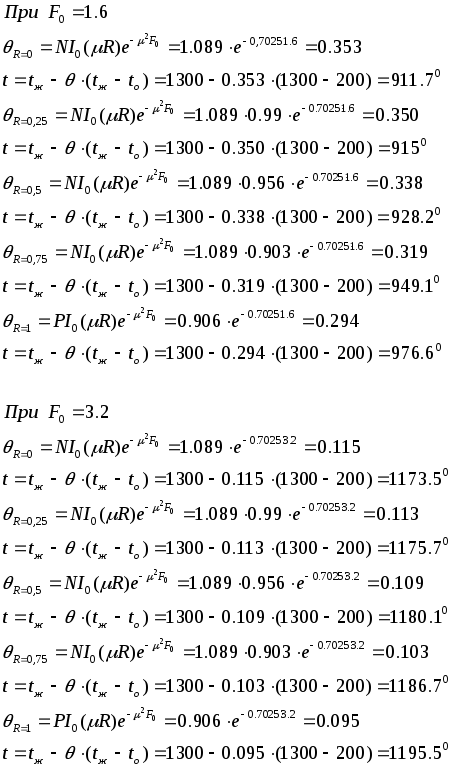
4._Определение количества теплоты, подведённого к телу за весь период нагревания (в расчёте на 1 квадратный метр поверхности пластины)

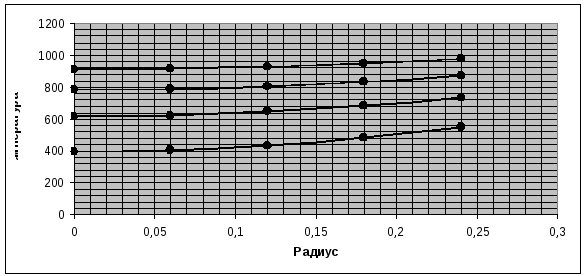
5._Графики, построенные по данным пунктов 2 и 3

Задача 2. Конвективный теплообмен при вынужденном продольном обтекании плоской поверхности

Плоская пластина м. обтекается продольным потоком жидкости (газа) со скоростью м/с. Температура набегающего потока . Задана температура поверхности пластины . Найти:

1. Критическую координату 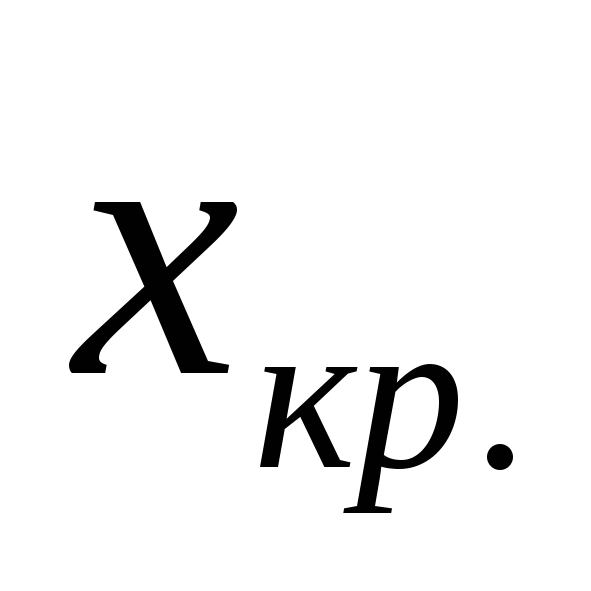точки перехода ламинарного пограничного слоя в турбулентный;

2. Толщины динамического и теплового 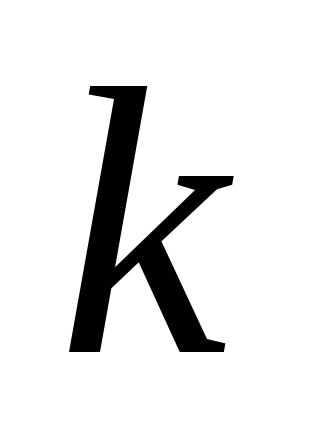пограничных слоёв на различных расстояниях от передней кромки поверхности;

3. Значения местных коэффициентов теплоотдачи 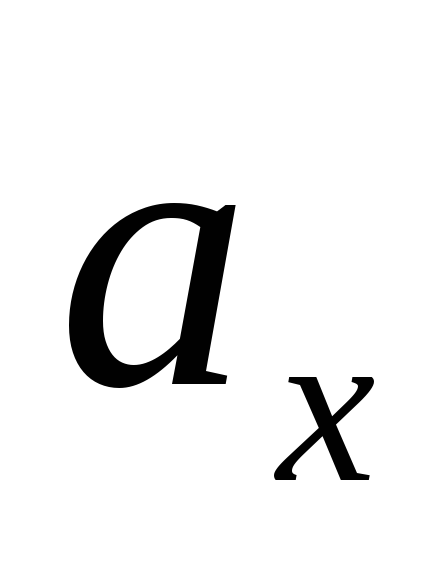на различных расстояниях от передней кромки пластины;

4. Средние коэффициенты теплоотдачи для участков с различными режимами течения;

5. Построить графики , , .

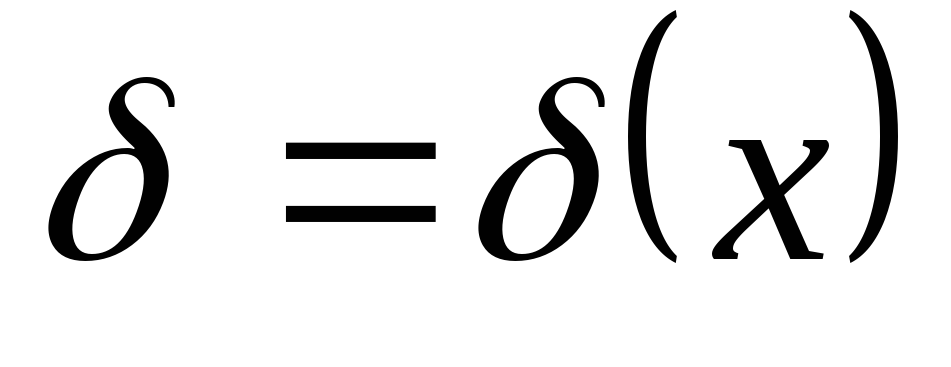1. Вычисление критической координаты точки перехода ламинарного пограничного слоя в турбулентный

Определим теплофизические параметры ТМ при температуре :

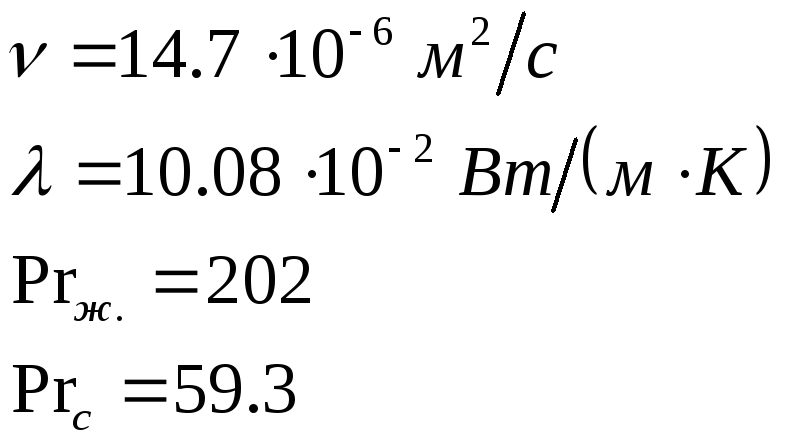
Вычислим число Рейнольдса:

Критическое число Рейнольдса:

Т.к. , то режим течения в пограничном слое на конце пластины - турбулентный.

Вычислим координату точки перехода ламинарного течения в пограничном слое в турбулентное:

2. Вычисление толщин динамического и теплового пограничных слоёв на различных расстояниях от передней кромки поверхности

2.1. Расчёт ламинарного режима течения

2.1.1. Вычисление толщин динамического и теплового пограничных слоёв, а также коэффициентов теплоотдачи для различных точек

Для точки вычислим:

Для других точек ламинарного режима течения вычисления производим по этим же формулам, результаты записываем в таблицу.

2.1.2. Вычисление среднего коэффициента теплоотдачи и плотности теплового потока

2.2. Расчёт турбулентного режима течения

2.2.1. Вычисление толщины динамического пограничного слоя, а также коэффициентов теплоотдачи для различных точек

Для точки вычислим:

Для других точек турбулентного режима течения вычисления производим по этим же формулам, результаты записываем в таблицу

2.2.2. Вычисление среднего коэффициента теплоотдачи и плотности теплового потока

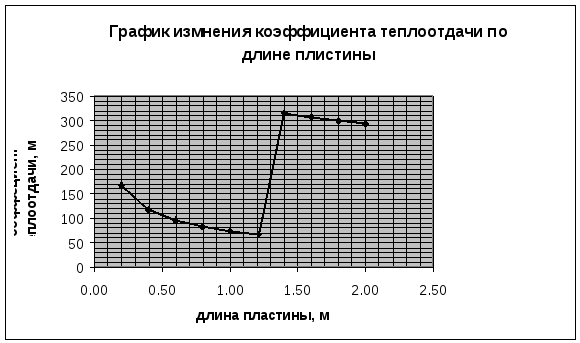
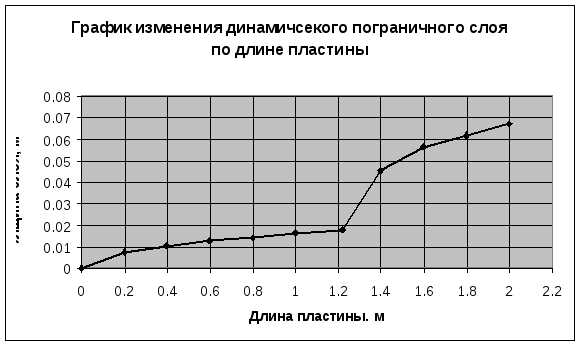
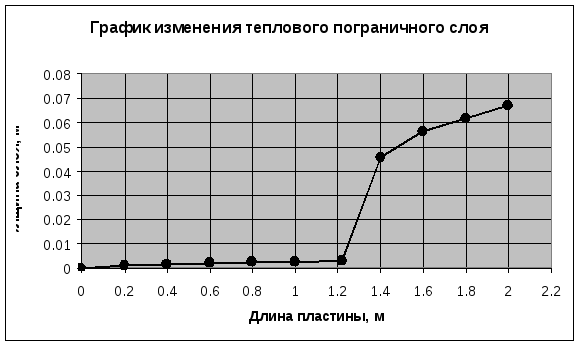
2.3. Результаты вычислений

	Ламинарный						Турбулентный
	0,2	0,4	0,6	0,8	1	1,22	1,4	1,6	1,8	2
	1,63	3,26	4,89	6,53	8,16	9,95	11,4	13,0	14,7	16,3
	0.0072	0.0102	0.0126	0.0145	0.0162	0.0179	0.0454	0.0562	0.0617	0.0671
	0,0013	0.0018	0.0022	0.0025	0.0028	0.0031	0.0454	0.0562	0.0617	0.0671
	331.79	469.23	574.68	664.1	742.37	819.76	4375.08	4859	5361.9	5823.9
	167.22	118.25	96.54	83.67	74.83	67.73	315	306.12	300.27	293.52

Построение графиков по результатам вычислений

Задача 3. Теплообмен излучением между газом и твёрдой ограждающей поверхностью

Вычислить плотность теплового потока, обусловленного излучением дымовых газов к поверхности газохода сечением . Состав газов задан. Общее давление газа . Температура газов на входе в газоход и на выходе . Средняя температура поверхности газохода .

Степень черноты чугуна окисленного:

Вычислим приведённую степень черноты чугуна окисленного:

Вычислим среднюю температуру газов по тракту:

Средняя длина пути луча:

Парциальные давления двуокиси углерода и водяного пара:

Первый метод (с использованием диаграмм)

Произведение парциального давления на двуокиси углерода и водяного пара на длинну луча:

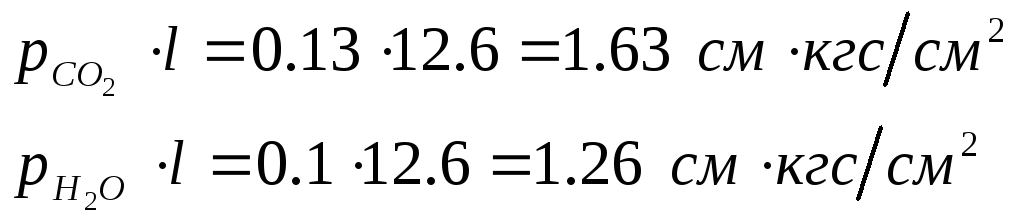
По графикам определяем степени черноты двуокиси углерода и водяного пара:

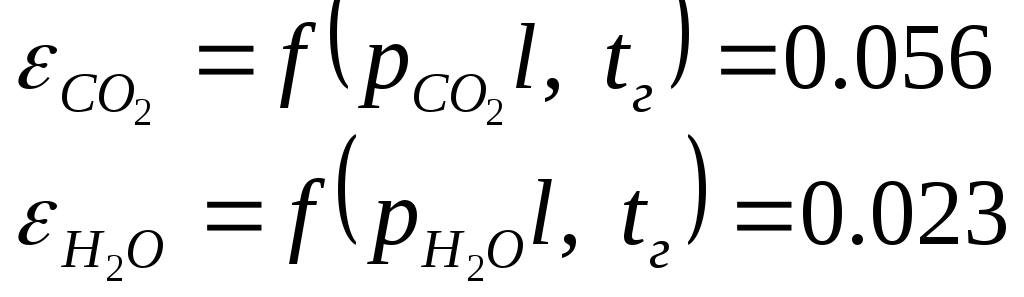
По графику определяем поправочный коэффициент на парциальное давление для водяного пара:

Степень черноты газовой смеси:

По графикам определяем степени черноты двуокиси углерода и водяного пара по температуре стенки :

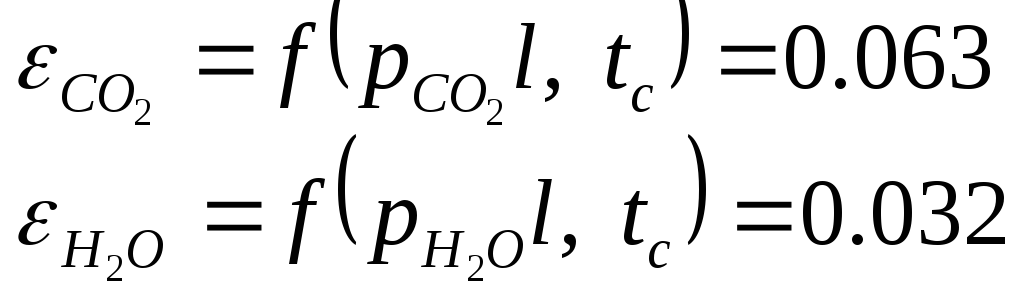
Поглощательная способность газовой смеси:

Плотность теплового потока:

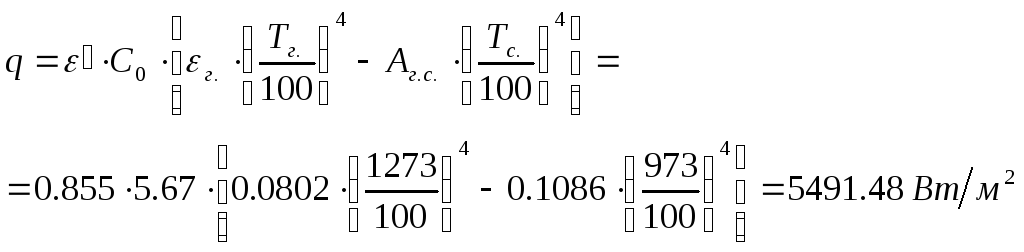
Второй метод (аналитический)

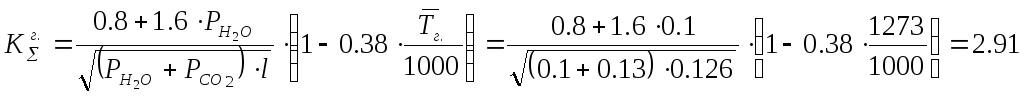
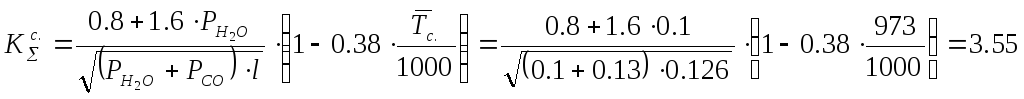
Суммарное парциальное давления водяного пара и двуокиси углерода:

Степень черноты газовой смеси:

Поглощательная способность газовой смеси:

Плотность теплового потока:

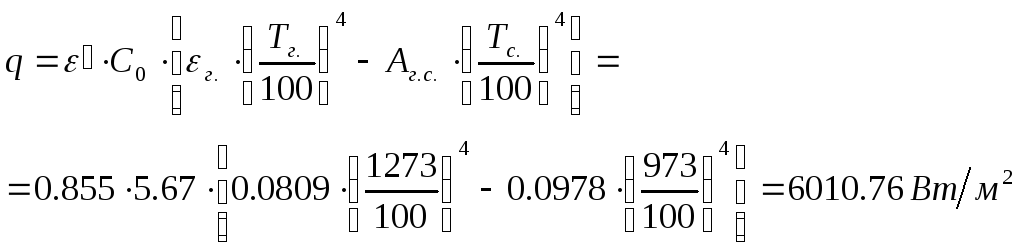
Задача 4. Тепловой расчёт экономайзера

Змеевиковый экономайзер парового котла предназначен для подогрева питательной воды в количестве от температуры до . Вода движется верх по трубам диаметром . Коэффициент теплопроводности материала стенки . Средняя скорость движения воды .

Дымовые газы () движутся сверху вниз в межтрубном пространстве со средней скоростью в узком сечении трубного пучка . Расход газов . Температура газов на входе в экономайзер , на выходе (одна из четырех температур неизвестна). Задано расположение труб в пучке (шахматное или коридорное) и относительные шаги: поперечный и продольный . Со стороны газов поверхность труб покрыта слоем сажи толщиной , со стороны воды – слоем накипи толщиной . Коэффициенты теплопроводности принять: для сажи , для накипи

Определить поверхность нагрева, количество и длину отдельных секций (змеевиков)

Схема движения теплоносителей в экономайзере