Курсовая работа по тепломассообмену

─ 14 ─

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

МАГНИТОГОРСКИЙ ГОСУДАРСТВЕННЫЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Г.И.НОСОВА

КАФЕДРА ТЕПЛОТЕХНИЧЕСКИХ И ЭНЕРГЕТИЧЕСКИХ СИСТЕМ

КУРСОВАЯ РАБОТА

ПО ТЕПЛОМАССООБМЕНУ

ВЫПОЛНИЛ:	студент гр. Эт-06-1 Бураншин З.А
ПРОВЕРИЛ:	ст. преподаватель, д.т.н. Матвеева Г.Н.

МАГНИТОГОРСК

2008

Задача 1. Нестационарная теплопроводность

Металлическая заготовка, имеющая форму пластины (циллиндра), неограниченной длинны, с начальной температурой , нагревается в печи, температура которой поддерживается постоянной до конечной температуры по оси заготовки . Считая длинну (и высоту) заготовки большими большими по сравнению с толщиной, определить:

1. Время нагревания заготовки до данной конечной температуры;

2. Температуры на оси и на поверхности заготовки для различных моментов времени (с использование монограмм Будрина);

3. Распределение температуры по толщине заготовки для четырёх моментов времени (с использованием аналитических формул);

4. Количество теплоты, подведённой к телу в течении всего периода нагревания (на 1 поверхности пластины или на 1 длинны циллиндра);

5. По результатам (2) и (3) построить графики.

Форма тела: ЦИЛИНДР

Материал: СТАЛЬ У12

1._Определение времени нагревания заготовки до конечной температуры

Сначала найдем из справочных таблиц теплофизические параметры пластины (теплоёмкость, коэффициент теплопроводности, коэффициент температуропроводности и плотность) при начальной температуре и конечной температуре центра пластины , и вычислим их средние значения:

Параметр			Среднее
	0,544	0,695	0,62
	37,2	27,2	32,2
	0,029	0,021	0,025
	7,713	7,388	7,55

Вычислим число и безразмерную температуру для центра пластины в последний момент времени нагрева:

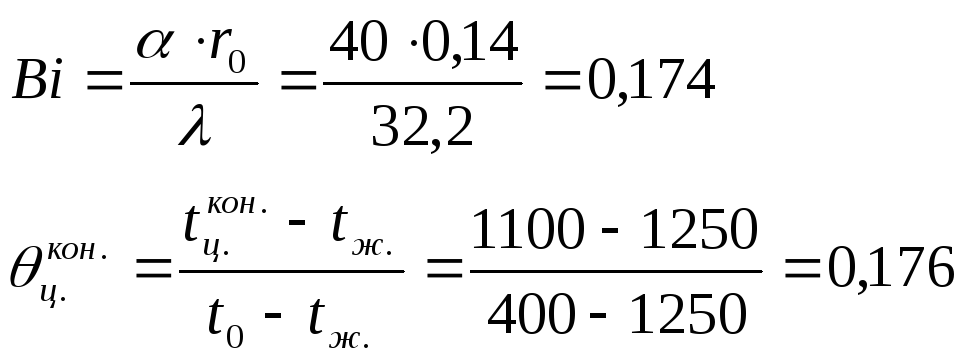
По номограмме Будрина для центра пластины определим:

Вычислим время нагревания заготовки:

2._Определение температур на оси и на поверхности заготовки для различных моментов времени

Интервал времени нагревания заготовки разобьём на несколько промежутков. Для каждого значения вычислим время (в часах), найдём безразмерные температуры в центре и на поверхности пластины по номограммам Будрина (в зависимости от и ). По безразмерным температурам вычислим температуры в центре и на поверхности пластины в градусах Цельсия.

Для :

1. Время нагревания

2. Безразмерная температура в центре пластины (определяем по соответствующей диаграмме Будрина в зависимоси от и ):

3. Безразмерная температура на поверхности пластины (определяем по соответствующей диаграмме Будрина в зависимоси от и ):

4. Температура на оси циллиндра:

5. Температура на поверхности циллиндра:

Для остальных значений критерия Фурье вычисления производим по этим же формулам, результаты вычислений заносим в таблицу.

	0,5	1	1,5	2	3	4	5,45
	0,39	0,78	1,18	1,57	2,35	3,14	4,27
	0,94	0,76	0,65	0,55	0,38	0,27	0,176
	0,9	0,68	0,58	0,54	0,36	0,26	0,16
	451	604	698	783	927	1021	1100
	485	672	757	791	944	1029	1114

3._Определение распределения температуры по толщине заготовки для четырёх моментов времени

При определяем из таблиц:

При

При

При

Найдём безразмерные температуры в момент времени

Температура для этой точки:

Для остальных точек и в другие моменты времени вычисления производим аналогичным образом, результаты записываем в таблицу.

	0,8825	0,5353	0,3836	0,1695
	500	798	926	1107
	0,8774	0,5322	0,3814	0,1686
	504	803	929	1108
	0,8675	0,5262	0,3771	0,1667
	513	803	929	1108
	0,841	0,5102	0,3656	0,1616
	535	816	939	1113
	0,81	0,4915	0,3522	0,1557
	562	832	951	1118

4._Определение количества теплоты, подведённого к телу за весь период нагревания (в расчёте на 1 метр длинны цилиндра)

Полное количество теплоты, которое было бы подведено к цилиндру (на 1 метр её длинны), если бы нагревание длилось до наступления полного теплового равновесия между цилиндром и воздухом печи:

Средняя безразмерная температура в последний момент времени нагрева:

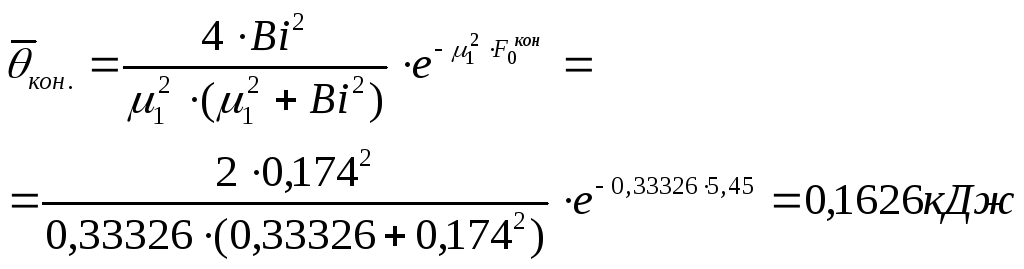
Полное количество теплоты, подведённого к цилиндру (на 1 метр её длинны) за весь период нагрева:

5._Графики, построенные по данным пунктов 2 и 3

Задача 2. Конвективный теплообмен при вынужденном продольном обтекании плоской поверхности

Плоская пластина м. обтекается продольным потоком жидкости (газа) со скоростью м/с. Температура набегающего потока . Задана температура поверхности пластины . Найти:

1. Критическую координату точки перехода ламинарного пограничного слоя в турбулентный;

2. Толщины динамического и теплового пограничных слоёв на различных расстояниях от передней кромки поверхности;

3. Значения местных коэффициентов теплоотдачи на различных расстояниях от передней кромки пластины;

4. Средние коэффициенты теплоотдачи для участков с различными режимами течения;

5. Построить графики , , .

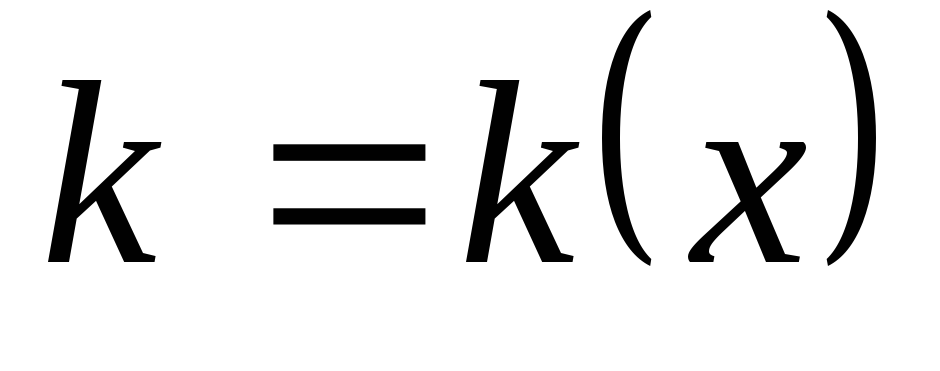Жидкость: Воздух

1. Вычисление критической координаты точки перехода ламинарного пограничного слоя в турбулентный

Определим теплофизические параметры воздуха при температуре :

Определим число Прандтля воздуха при температуре :

Критическое число Рейнольдса:

Вычислим координату точки перехода ламинарного течения в пограничном слое в турбулентное:

2. Вычисление толщин динамического и теплового пограничных слоёв на различных расстояниях от передней кромки поверхности

2.1. Расчёт ламинарного режима течения

2.1.1. Вычисление толщин динамического и теплового пограничных слоёв, а также коэффициентов теплоотдачи для различных точек

Для точки вычислим:

Для других точек ламинарного режима течения вычисления производим по этим же формулам, результаты записываем в таблицу.

2.1.2. Вычисление среднего коэффициента теплоотдачи и плотности теплового потока

2.2. Расчёт турбулентного режима течения

2.2.1. Вычисление толщины динамического пограничных слоя, а также коэффициентов теплоотдачи для различных точек

Для точки вычислим:

Для других точек турбулентного режима течения вычисления производим по этим же формулам, результаты записываем в таблицу.

2.2.2. Вычисление среднего коэффициента теплоотдачи и плотности теплового потока

2.3. Результаты вычислений

Параметр	Ламинарный участок					Турбулентный участок
	0,1	0,4	0,7	1	1,38	1,4	1,8	2,2	2,6	3
	7242	28968	50693	72419	100000	101386	130353	159321	188289	217256
	0,0055	0,011	0,015	0,017	0,019	0,052	0,063	0,074	0,085	0,095
	0,006	0,0125	0,017	0,0193	0,0216	0,052	0,063	0,074	0,085	0,095
	24,79	49,57	65,58	78,38	92,1	252,5	308,7	362,5	414,3	465
	11,4	5,7	4,31	3,61	3,07	8,296	7,889	7,58	7,33	7,13
	184,2					315,6
	6,14					7,645
	921					1146,75

3. Построение графиков по результатам вычислений

График изменения коэффициента теплоотдачи

Задача 3. Тепловой расчёт пароперегревателя

В пароперегреватель поступает сухой насыщенный водяной пар. Пар движется по стальным трубам диаметром . Коэффициент теплопроводности стали . Средняя скорость движения пара , расход пара , давление . Температура и энтальпия перегретого пара соответственно и . Дымовые газы (13% и 11% ) в количестве движутся вдоль трубного пучка. Температура газов на входе . Средняя скорость газов в узком сечении пучка . Заданы расположение труб (шахматное или коридорное) и относительные шаги: поперечный и продольный . Со стороны газов трубы пароперегревателя покрыты слоем сажи толщиной . Теплопроводность сажи можно принять . Изменением давления по длинне пароперегревателя в расчётах можно пренебречь.

Определить поверхность нагрева, количество и длину змеевиков пароперегревателя парового котла. Схема движения теплоносителей в пароперегревателе показана на рисунке.

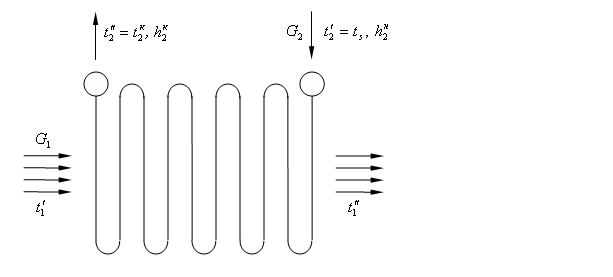
Рис. Схема движения теплоносителей в пароперегревателе.

Дымовые газы: Водяной пар:

Коэффициент теплопроводности стенки: Диаметры труб: Расположение труб: шахматное

Поперечный относит. шаг: Продольный относит. шаг: Слой сажи: Коэффициент теплопроводности сажи: