
задания / Инф.каскады / Information_Cascades_and_Expert_Opinion_web
.pdfИнформационные каскады и экспертное мнение: лабораторный эксперимент
А.А. Коновалов, Е.В. Попов
Институт экономики УрО РАН
Аннотация
В статье представлены результаты серии экспериментов, посвященных проблеме влияния экспертов на устойчивость информационных каскадов. Авторы модифицировали эксперимент Anderson and Holt (1997), разделив участников на два типа с разной точностью частного сигнала. Результаты подтвердили неустойчивость классических информационных каскадов, но показали, что введение агентов-«экспертов», обладающих более точным сигналом, о котором осведомлены остальные участники эксперимента, приводит к росту вероятности появления каскада. Показано, что агенты, принимавшие решение до «экспертов», совершали меньше ошибок с точки зрения байесовской модели, при этом участники, принимавшие решение после, чаще формировали каскад, что может служить объяснением невыской доли верных решений среди этой категории участников.
В своей классической статье Бикчандани, Хиршлайфер и Уэлш показали, что стадное поведение может иметь рациональную основу (Bikhchandani et al., 1992). Если агенты принимают байесовские решения в очереди, заданной экзогенно, основываясь на собственном частном сигнале и наблюдаемом выборе других, то в определенный момент для одного из них (и всех последующих) будет более рационально отказаться от выбора по собственному сигналу и ориентироваться на действия большинства. С этого момента возникает информационный каскад: агенты игнорируют частные сигналы, руководствуясь байесовским принципом выбора. Anderson and Holt (1997) провели первое экспериментальное исследование, подтвердившее возможность формирования информационных каскадов в лабораторных условиях.
Бикчандани, Хиршлайфер и Уэлш отмечали, что агенты с более высокой точностью сигнала («лидеры моды») могут прервать информационный каскад. При байесовском выборе их мнение будет обладать большим влиянием, нежели агрегированный выбор «обычных» агентов. В данном исследовании мы представляем экспериментальные результаты, связанные с появлением в очереди агентов-«экспертов», оценивая их влияние на формирование или свертывание информационных каскадов.
Мы воспроизводим эксперимент Anderson and Holt (1997), разделив его на две сессии. Первая (контрольная) — типичная игра типа
1
observational learning с бинарным выбором: агенты угадывают одну из двух урн, поочередно извлекая из нее черные и белые шары. Ее структура — очередь из девяти участников, обладающих точностью сигнала, равной 0.6. Во второй сессии экспериментаторы случайным образом выбирали одного из агентов, повысив точность его частного сигнала до 0.9 и сообщив об этом остальным участникам.
Результаты эксперимента показали, что в случае участия экспертов (высокоинформированных игроков) информационные каскады возникают в 73% случаев (в контрольной сессии — в 25%). При этом процент верных решений остается на том же уровне. Вероятно, это связано с высокой долей неверных каскадов (18%) в экспериментах с участием экспертов. Тем не менее эконометрический анализ с использованием логит-функции ошибок показал, что агенты, принимавшие решения до агентов-«экспертов», чаще следовали байесовской модели принятия решений. Впрочем, ни в одном из раундов второй сессиии эксперимента каскад не возникал до выбора агента-«эксперта». При этом обусловленные их выбором каскады были достаточно устойчивыми, и вторая сессия демонстрирует большую глубину этих каскадов (глубиной мы называем разницу между числом агентов, выбравших один из двух вариантов).
Полученные результаты согласуются с достаточно обширным числом экспериментальных работ в области информационных каскадов. Среди них первые эксперименты (Anderson and Holt, 1997), исследования влияния размера платежей(Anderson, 2000), институционального дизайна (Hung and Plott, 2001), эксперименты в приложении к рынку труда (Kurbler and Weizsacker, 2003), сетевым структурам (Choi et al., 2004) и другие. Alevy et al. (2007) показали, что профессионалы по сравнению с лабораторными испытуемыми (обычно студентами) склонны больше доверять собственному сигналу, нежели выбору окружающих. Наши результаты подтверждают выводы работы Goeree et al. (2007), в которой показано, что информационные каскады весьма неустойчивы и носят исключительно локальный характер. Авторы показывают, что экспериментальные результаты лучше согласуются не с традиционной байесовской моделью, но с концепцией QRE-равновесия (quantal response equilibruim). Аналогичные наблюдения представлены
встатье Choi et al. (2004). В работе Ziegelmeyer et al. (2010)также представлены два типа агентов — слабо- и высокоинформированные. Авторы отмечают, что агенты с низкой точностю сигнала склонны к поведению, предсказываемому равновесной моделью, тогда как высокоинформированные участники эксперимента отклоняются от этой модели, и редко вызывают свертывание каскада (не более чем
в15% случаев). В работе Sasaki (2007) представлены результаты эксперимента, в котором точность сигнала в очереди игроков либо возрастает, либо снижается. Автор отмечает, что во втором случае участники делают более точные предсказания.
Среди других наблюдений: наши результаты подтверждают, что следование байесовскому правилу не является наиболее эффективной стратегией, поскольку участники эксперимента действуют далеко не рационально. Это согласуется с результатами мета-исследования, представленного в работе Weizsacker (2008).
2

В первой части статьи представлена базовая модель информационных каскадов и дизайн проведенного эксперимента. Вторая и третья части содержит эмпирические результаты и эконометрические оценки, в заключении содержатся выводы и потенциальные направления будущих исследований.
1Информационные каскады с участием экспертов
Опишем классическую модель информационных каскадов Бикчандани, Хиршлайфера и Уэлша (далее BHW-модель) и экспериментальный дизайн. Природа случайным образом ( = 0.5) выбирает одно из двух состояний мира = ( , ). Состояние мира реализуются с помощью двух урн, отмеченных и и содержащих белые и оранжевые шары в разных соотношениях (три оранжевых и два белых для , два оранжевых и три белых для ). Выбранное состояние неизвестно игрокам, но они обладают общим знанием относительно( ) = 1 − ( ) = 0.5. Цель игроков — угадать истинное состояние мира .
Игроки случайным образом располагаются в экзогенно заданной очереди (1.. ). В -м раунде игрок получает частный сигнал = { , }, извлекая шар из урны и возвращая его на место ( — оранжевый шар,
— белый шар). Этот сигнал обладает точностью = 0.6 — сотношением белых и оранжевых шаров в урнах. Кроме того, каждый игрок обладает информацией о выборе, сделанном предыдущим игроками (1, ..., − 1). Эта информация формирует общий сигнал = { , }, где— число игроков, назвавших урну А (с учетом частного сигнала-го игрока), — урну (аналогично). Тогда -й игрок обладает апостерориорной верой:
( |
| |
( , )) = |
( , | ) · ( ) |
= |
|
|
|
|
( , ) |
||
|
|
= |
|
( , | ) · ( ) |
|
|
|
( , | ) · ( ) + ( , | ) · ( ) |
|||
|
|
|
|||
(1)
(2)
С учетом ( ) = ( ) = = 0.5 и точности , единой для всех игроков (Birchler and Butler, 2007):
( |
| |
( , )) = |
(1 − ) |
(3) |
|
(1 − ) + (1 − ) |
|||||
|
|
|
В BHW-модели рациональный игрок, принимающий байесовское решение, называет урну , если ( | ( , )) > 0.5, и , если( | ( , )) < 0.5. В случае равенства вероятностей игрок следует частному сигналу. Подобная модель приводит к формированию информационного каскада (выбору одного и того же состояния мира при любом собственном сигнале) с очень высокой вероятностью уже для первых игроков (для пятого игрока вероятность следования частному сигналу меньше 5% (Ziegelmeyer et al., 2010)).
3

Таблица 1: Общие результаты экспериментов
|
Эксперимент с участием |
Контрольный |
|
экспертов |
эксперимент |
|
|
|
|
|
|
Всего принятых решений |
135 |
108 |
|
|
|
Правильные решения |
63,7% |
61,6% |
(%), из них: |
|
|
|
|
|
соответствующие |
63,7% |
58,3% |
частной информации; |
|
|
|
|
|
по Байесу |
70,3% |
57,5% |
|
|
|
Информационные |
73% |
25% |
каскады (%), из них |
|
|
|
|
|
верных |
82% |
100% |
Во второй сессии эксперимента среди игроков случайным образом выбирался агент-«эксперт», для которого распределение шаров в урнах было изменено. Урна содержала один белый шар и четыре оранжевых, урна — четыре белых и один оранжевый. Таким образом, точность сигнала для этого игрока повышалась до = 0.8. Повышенная точность сигнала в ряде раундов приводила к смене рациональной веры на противоположную и приводила к возникновению каскада.
Эксперименты состояли из двух сессий, в которых приняли участие 70 студентов экономических специальностей Уральского государственного университета им. А.М. Горького, не имевших подготовки в области теории игр или экономики информации. В каждой сессии случайным образом отбирались девять участников, которые использовали компьютеры с установленным экспериментальным интерфейсом, созданным в программном пакете zTree (Fischbacher, 2007). Первая сессия состояла из 12 периодов, вторая — из 15 периодов, в каждом из которых 9 участников делали свой выбор. Перед началом экспериментов участники знакомились с правилами игры и участвовали в пробном раунде. Перед компьютерным экспериментом принципы игры демонстрировались на физических объектах. Впоследствии выбор урны и частного сигнала осуществлялись с помощью генератора случайных чисел. Каждый участник мог наблюдать на своем мониторе изображение урн, частный сигнал и выбор остальных игроков, после чего принимал решение с помощью мыши. В сессии с участием «экспертов» игрок с более высокой точностью сигнала объявлялся остальным участникам. Участники, верно угадавшие тип урны, получали вознаграждение в размере 25 рублей за раунд.
4

2Экспериментальные результаты
Общие результаты экспериментальных сессий представлены в таблице 1. В обеих сессиях уровень правильных ответов был примерно одинаков: 62 — 63%. При этом в эксперименте с участием экспертов игроки чаще выбирали в соответствии с правилом Байеса (или счетом большинства) и чаще следовали собственному сигналу (63,7% против 58,3%). Основной результат: если в базовом эксперименте, повторяющем дизайн Anderson and Holt (1997) (с уменьшенной точностью сигнала и увеличенной до девяти человек длиной очереди), каскады наблюдались лишь в 25% случаев, то в эксперименте с участием агентов-«экспертов» в 73% случаев выбор эксперта приводил к формированию каскада, соответствующего этому выбору. В 18% случаев этот выбор был неверным. Таким образом, появление агента-«эксперта» с точностью сигнала, близкой к 1, однозначно стимулировало испытуемых к копированию выбора эксперта, в незавимимости от выбора предыдущих участников. В более поздних раундах эксперимента этот эффект начинает проявляться все более явно. Общий доход участников в базовом эксперименте составил 84% от максимального общего дохода (если бы все агенты принимали байесовские решения), в эксперименте с экспертами — 92% от максимального.
Следуя Anderson and Holt (1997), мы рассчитали реальную эффективность принятых решений и эффективность частного сигнала
— выигрыш потенциальных решений, которые могли бы быть приняты исключительно на основании частного сигнала. Реальная эффективность равна разнице между действительным выигрышем участников и выигрышем , которые они получили бы в случае рандомизированного принятия решений (просто подкидывая монету), с нормализацией по разнице между оптимальным выигрышем (на основании байесовских решений) и рандомным выигрышем. Эффективность равна 100%, если все решениях, следующих правилу Байеса, и 0% при случайных решениях:
= |
− |
% |
(4) |
|
− |
|
|
В первой сессии эксперимента мы получили крайне низкую реальную эффективность — 36.8%, тогда как в сессии с участием экспертов она достигла уровня в 56.9%; решения около 70% участников соответствовали байесовским (в первой сессии — 57.5%).
Эффективность частного сигнала показывает, насколько ожидаемый выигрыш при следовании частному сигналу превосходит случайный ( — ожидаемый выигрыш при следовании частному сигналу):
= |
− |
% |
(5) |
|
− |
|
|
Первая сессия показала более высокую эффективность частного сигнала в 47.3%, во второй сессии этот показатель составил 29.2%. Таким образом, в случае появления высокоинформированных игроков более эффективной стратегией является следование байесовским
5

Рис. 1: Зависимость между вероятностью выигрыша и номером
участника в очереди
|
.8 |
|
|
|
|
|
|
.7 |
|
|
|
|
|
of Win |
.6 |
|
|
|
|
|
Probability |
.5 |
|
|
|
|
|
|
.4 |
|
|
|
|
|
|
.3 |
2 |
4 |
6 |
8 |
10 |
|
0 |
|||||
|
|
|
Player Number |
|
|
|
|
|
With experts |
|
|
|
|
|
|
|
No experts |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
Таблица 2: Частичные результаты эксперимента с участием агентов- «экспертов»
Раунд |
Урна |
|
Номер участника: решение (сигнал) |
|
Результат |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
B |
4: A (b) |
5: A (b) |
6: B (a) |
7*: B |
8: B (b) |
9: B (a) |
Локальный |
|
|
|
|
|
(b) |
|
|
каскад |
|
|
|
|
|
|
|
|
|
5 |
B |
4: A (a) |
5 : B |
6*: B |
7: В (a) |
8: B (a) |
9: B (a) |
Явный каскад |
|
|
|
(b) |
(b) |
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
B |
4: A (b) |
5: B (b) |
6: A (a) |
7: A (a) |
8:A (b) |
9*:A (b) |
Неверный |
|
|
|
|
|
|
|
|
каскад |
|
|
|
|
* — «Эксперт» |
|
|
|
|
правилам, нежели ориентация на слабый частный сигнал. На рис. 1 представлены зависимости между средней вероятностью выигрыша и номером участника в очереди для обеих сессий эксперимента.
Втаблице 2 представлены некоторые результаты эксперимента
сучастием экспертов. Мы используем терминологию, введенную Goeree et al. (2007). Локальный каскад — это каскад небольшой продолжительности, направление которого было впоследствии изменено; это наиболее часто встречающийся тип каскада (Goeree et al. (2007)показали, что в случае низкой точности сигнала и длинной очереди такие каскады появляются в 96 — 98% случаев). Такой тип каскада наблюдался в раунде 2 еще до появления эксперта. Явный каскад — каскад, соответствующий BHW-модели, когда все участники отказываются от собственного сигнала в пользу выбора большинства. Пример — пятый раунд эксперимента. Наконец, некоторые результаты подтверждают, что эксперт не всегда способен изменить направление каскада, но следует ему — см. раунд 6, в котором эксперт, делавший выбор последним, отказался от следования частному сигналу.
6

Рис. 2: Зависимость между средней глубиной каскада и номером
участника в очереди
4 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
Av. |Nb−Na| |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
|
|
Number in line |
|
|
|
|
|
|
|
With experts |
|
No experts |
|
|
|
По сравнению с базовым экспериментом каскады во второй сессии имели большую глубину. Следуя Ziegelmeyer et al. (2010), под глубиной мы понимаем | − |, где — число агентов, выбравших урну , а — число агентов, выбравших урну . Эта величина показывает смещение по сравнению с ситуацией, когда агенты делают выбор наугад, и общее мнение стремится к одной из альтернатив; она не является однозначным показателем информационного каскада, но служит косвенным подтверждением. В обеих сессиях наблюдалось отклонение от медианного распределения, но только в сессии с «экспертами» к концу раунда (девятому номеру участника) наблюдались однозначные явные каскады (см. рис. 2).
В течение второй сессии эксперимента участники, принимавшие решение после «экспертов» (вследствие случайного распределения таких решений оказалась ровно половина), следовали байесовскому решению так же часто, как и участники, делавшие выбор до них (примерно в 68% случаев). При этом первые реже следовали собственному сигналу (51,6%), чем последние (71,6%). Более того, вероятность следования частному сигналу для игроков во второй сессии статистически значимо снижалась при при увеличнии номера участника в очереди. Для контрольной сессии никакой значимой зависимости не наблюдалось (см. рис. 3). Сами «эксперты» продемонстрировали относительно низкий процент байесовских решений (66%, см. таблицу 1 в приложении). При этом в 86% случаев они сделали правильный выбор, что гораздо выше средних по эксперименту 64%.
3Оценка ошибок
Для оценки ошибок при выборе урн в экспериментах мы используем логистическую GLM-модель, связывающую реальную эмпирическую вероятность выбора урны A в экспериментах ( )
7
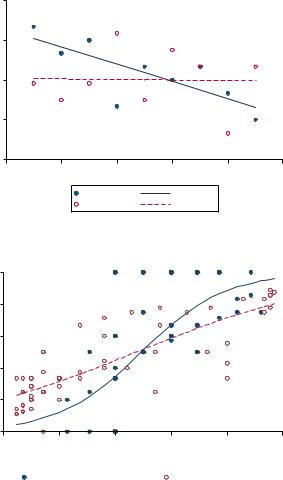
Рис. 3: Зависимость между вероятностью следования частному |
||||||
сигналу и номером игрока |
|
|
|
|
||
|
1 |
|
|
|
|
|
private signal |
.8 |
|
|
|
|
|
following |
.6 |
|
|
|
|
|
Probability of |
.4 |
|
|
|
|
|
|
.2 |
2 |
4 |
6 |
8 |
10 |
|
0 |
|||||
|
|
|
Number in line |
|
|
|
With experts |
Fitted OLS |
No experts |
Fitted OLS |
|
|
Рис. 4: Логит-оценка ошибок |
|
|||
|
1 |
|
|
|
|
|
|
.8 |
|
|
|
|
|
said A |
.6 |
|
|
|
|
|
of people |
.4 |
|
|
|
|
|
% |
|
|
|
|
|
|
|
.2 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
.2 |
.4 |
.6 |
.8 |
1 |
|
|
|
Probability of Urn A |
|
|
|
|
Logit estimate (Before experts) |
|
|
|
|
|
|
|
Logit estimate (After experts) |
|
|
|
|
|
|||||
|
Actual percentage |
|
|
|
|
|
|
|
Actual percentage |
|
|
|
|
|
|
|
|
|
|
и апостериорную вероятность ( ), предсказываемую байесовским решением. Логит-модель выглядит как возрастающая функция:
( ) = |
1 |
(6) |
|
|
|||
1 + − ( ) |
|||
|
|
Чем выше , тем ближе поведение участников эксперимента к рациональному. Как отмечают Anderson and Holt (2008), в случае совершенной рациональности эта функция имеет ступенчатый график: если вероятность, что в эксперименте используется урна , по Байесу больше 0.5, то игрок давать ответ , и B в случае если эта вероятность меньше 0.5. Соответственно, чем ближе график к вертикали, тем меньше отклонение поведения участников эксперимент от рациональности. На рис. 3 представлен график оценки для второй сессии эксперимента. Сплошная линия обозначает оценку логит-модели для
8

Таблица 3: Результаты логистической оценки
|
Эксперимент |
|
(1) |
(2) |
(3) |
(4) |
(5) |
|
|
|
|
|
|
|
|
|
|
|
|
|
3.08 |
3.49 |
6.73 |
2.82 |
3.29 |
|
|
|
|
|
|
|
|
|
|
|
(Стандартная ошибка) |
(0.97) |
(0.77) |
(2.06) |
(0.96) |
(0.60) |
|
|
|
|
|
|
|
|
|
||
|
Log-likelihood |
|
-55.73 |
-60.11 -26.86 -24.92 |
-116.16 |
|
||
|
|
|
|
|
|
|
|
|
|
Число ошибок, % |
42.5 |
29.6 |
31.7 |
30 |
35.7 |
|
|
|
|
|
||||||
|
Таблица 4: Результаты оценки линейных регрессий |
|||||||
|
Эксперимент |
|
(1) |
(2) |
|
(3) |
(4) |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
0.71 (0.08) |
0.77 (0.07) |
1.33 (0.20) |
0.64 (0.05) |
|||
|
|
|
|
|
|
|||
|
|
0.13 (0.05) |
0.15 (0.04) |
-0.17 (0.11) |
0.20 (0.03) |
|||
|
|
|
|
|
|
|
|
|
Число наблюдений |
|
120 |
135 |
|
60 |
60 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0.36 |
0.48 |
|
0.44 |
0.69 |
|
|
Стандартные ошибки даны в скобках
участников, принимавших решение до игроков-«экспертов», пунктирная — для участников, принимавших решений после экспертов. Наиболее сильные отклонения от рациональности наблюдаются в районе 50-процентной вероятности, при этом более рационально вели себя участники, принимавшие решение до экспертов.
Результаты эконометрической оценки логистической модели представлены в таблице 3, где (1) базовый эксперимент (первая сессия),
(2) эксперимент с участием экспертов (вторая сессия), (3) участники, принимавшие решения до экспертов во второй сессии, (4) участники, принимавшие решения после экспертов во второй сессии, (5) результаты всего эксперимента (две сессии). Оценочные кривые изображены на рис. 1 приложения.
Данные эксперимента в целом свидетельствуют скорее о линейной, нежели логистической зависимости между эмпирической и байесовской вероятностью: участники редко склонны к рациональным решениям, и в случае небольших отклонений от 50-процентной теоретической вероятности эмпирическая вероятность отклоняется соответствующим образом. Оценим простейшей линейной регресией связь эмпирической и теоретической вероятностей выбора урны А:
( ) = ( ) + + |
(7) |
На общих данных эксперимента эта регрессия показывает 2 = 0.43
и дает следующее уравнение: |
|
( ) = 0.74 ( ) + 0.14 |
(8) |
Результаты оценки линейных регрессий между эмпирической и теоретической вероятностью даны в таблице 4: (1) базовый эксперимент, (2) эксперимент с участием экспертов, (3) участники,
9
принимавшие решения до экспертов во второй сессии, (4) участники, принимавшие решения после экспертов во второй сессии. Оценки участников, принимавших решение после игроков-«экспертов», лучше ложатся в линейную модель: они менее рациональны в байесовском смысле, но эмпирическая вероятность выбора верной урны очень близка к теоретической.
Таким образом появление высокоинформированных участников стимулировало игроков к отказу от следования собственному сигналу и следованию сигналу эксперта вне зависимости от выбора предыдущих игроков, что почти всегда приводило к формированию каскада. Среди участников, принимавших решение после «эксперта», почти 77% следовали его выбору, 70% принимали решению, соответствующее байесовскому, и лишь 52% следовали собственному сигналу.
4Заключение
Информационные каскады чрезвычайно редко возникают в лабораторных условиях, особенно если точность сигнала достаточно невелика (об этом свидетельствует, в частности, обширное исследование Goeree et al. (2007)). Гораздо более распространенный случай
— локальные каскады, которые достаточно быстро сворачиваются; впрочем, практически невозможно точно определить, что подобные короткие последовательности схожих выборов являются каскадами. Участники экспериментов не склонны к принятию рациональных решений следуют собственным сигналам — следовательно, рациональное следование байесовскому выбору в таких условиях вряд ли можно назвать эффективной стратегией.
Появление агентов с более высокой точностью сигнала определенно меняет ситуацию. При этом вряд ли будет справедливо утверждать, что их появление вызывает классический информационный каскад BHW-модели, основанный на байесовском принятии решений. Возникает каскад иного типа — подражание выбору агента-«эксперта», вера о точности сигнала которого достаточно высока. Поэтому для агентов, делающих выбор до «эксперта», коэффицент корреляции между выбором и частным сигналом равен 0.44, для выбирающих после — нет никакой статически значимой корреляции. В то же время наблюдается весьма сильная значимая корреляция с выбором высокоинформированного агента (0.55).
Таким образом мы можем предположить, что возникновение «лидеров моды» или участников рынка с высокой точностью сигнала нивелирует эффекты конформизма и следованию большинству, вызывая эффект подражания. При этом вполне возможно, что на определенном этапе влияние лидера уже не оказывает воздействия на игроков (они могут быть вообще не осведомлены о его существовании), и возникнет эффект традиционного каскада. В этом случае основная функция и характеристика «лидеров» — возможность не изменять направление каскадов, но создавать их.
10
