задания / Инф.каскады / СИНЕРГЕТИЧНІ ТА ЕКОНОФІЗИЧНІ МЕТОДИ ДОСЛІДЖЕННЯ - монографія Дербенцев, Сердюк, Соловьйов, Шарапов

Оскільки рівняння (2.6) є таким, що строго виконується лише для L і N , необхідно перевірити також відхилення від ідеального випадку, оскільки на практиці використовуються лише скінчені ряди. Виявляється, що для кількох найбільших (найменших) власних значень ефект впливу скінчених величин L і N відсутній.

Якщо звернути увагу на компоненти власних векторів, які відповідають найбільшим власним значенням, то ми пересвідчимося, що максимальному власному значенню відповідає власний вектор, компонентами якого є найбільш стійкі валюти. Наступним за максимальним власним векторам відповідають компоненти векторів, які містять регіональні валюти.

Обернене відношення участі

Визначившись з інтерпретацією найбільшого власного значення, що значно відхиляється від результатів ТВМ, зосередимось на дослідженні інших власних значень. Відхилення розподілу компонентів власного вектора

uk від ТВМ (Гаусового розподілу) більш явне, коли відстань від верхньої границі ТВМ k збільшується. Оскільки близькість до збільшує

ефекти невизначеності, необхідно виділити кількість компонентів, які „беруть значну участь” в кожному власному векторі, що, у свою чергу, відображає ступінь відхилення від ТВМ для розподілу компонентів власного вектора. Для цього використовується поняття оберненого відношення участі (ОВУ), що часто застосовується в теорії локалізації. ОВУ власного вектора

uk визначається як

t 1

де ulk , l 1,..., N – компоненти власного вектора uk . Значення I k може бути проілюстровано двома граничними випадками:

ii)вектор з одним компонентом u1k 1 і нульовими іншими має ik 1.

Таким чином, ОВУ визначає кількість даних з набору компонентів власного вектора (кількість елементів системи), що значно впливають на властивості системи в цілому, яка описана часовими рядами динаміки її елементів.

Наявність векторів з великими значеннями I k також виникає в теорії локалізації Андерсона. У контексті теорії локалізації часто знаходять „множину випадкових матриць”, що містять узагальнені стани з невеликими

I k в більшій частині спектра власних значень, тоді як основні стани

41

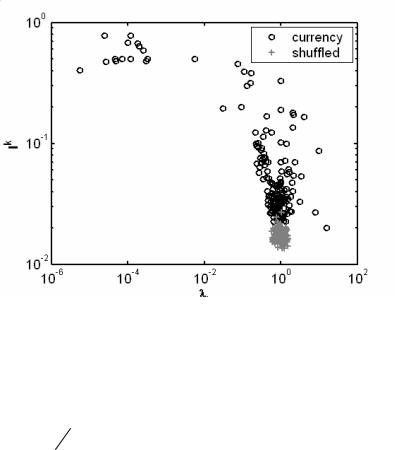
локалізовані і мають великі I k . Виявлення локалізованих станів для малих та великих власних значень матриці крос-кореляцій C нагадує про локалізацію Андерсона та припускає, що C може мати випадкову зону матричної структури.

На рис. 2.4 компоненти власних векторів випадкової матриці згруповані у вигляді вузької смужки. Навпаки, для валютної матриці мають місце значні відхилення оберненого відношення участі саме для тих власних значень, які лежать за межами .

Рис. 2.4. Обернене відношення участі для матриці крос-кореляцій, отриманої для валютного ринку, поданих з 1990 по 2010 рр., у порівнянні з випадковою матрицею (shuffled)

Інтерпретація власних значень та власних векторів, що відхиляються від ТВМ

Кількість істотних внесків у власний вектор визначається за допомогою ОВУ, для отримання ж загальних властивостей досліджуються

компоненти 1I k власного вектора uk . Безпосередній аналіз таких власних

векторів, однак, не приводить до прозорої інтерпретації їх економічного змісту. Щоб інтерпретувати їх значення, необхідно звернути увагу, що найбільше власне значення значно більше, ніж інші N 1 власні значення, тоді як розмірність матриці С є N N . Тому для аналізу власних векторів,

42

що відхиляються, необхідно видалити ефект найбільшого власного значення

max .

Щоб нівелювати ефект max , і, відповідно, Gmax t , для прибутковостей кожної акції Gi t складається рівняння регресії

або ж, у нашому випадку просте визначення тренду часового ряду, що відповідає max та вилучення його з кожної часової послідовності. Тоді

обчислюється матриця кореляції С, використовуючи формули (2.1)-(2.3).

учасників.

Далі проводиться аналіз істотних учасників іншої частини власних векторів. Результатами аналізу у нашому випадку є те, що кожний з власних векторів, що відхиляється від ТВМ, містить валюти, які належать валютам країн певного регіону, або країн торговельних партнерів. Ці власні вектори поділяють набір всіх валют у різні групи, що містять валюти найбільш розвинених країн (uN-1), а також регіональні коаліції (uN-2 – uN-9).

2.1.3 Кластерний аналіз на основі часових рядів

Головна ідея кластерного аналізу на основі часових рядів полягає в дослідженні кількох часових послідовностей одночасно, тобто, дослідження зміни коефіцієнта кореляції прибутковостей пар індексів i та j з плином часу згідно з (2.1) – (2.3).

Побудова матриці відстаней на основі матриці крос-кореляцій

Для отримання інформації з часових рядів, яку можна інтерпретувати з точки зору топологічної структури досліджуваної системи, необхідно спочатку визначити метрику, в межах якої проводитиметься інтерпретація. В якості функції від коефіцієнтів кореляції можна використати узагальнену відстань, експериментальним визначенням якої є

ij

Замість (2.10) можна використовувати також формулу:

43

У цьому випадку d i, j чисельно задовольняє трьом аксіомам Евклідової метрики:

(i)d i, j 0 якщо і лише якщо i=j;

(ii)d i, j d j,i ;

(iii)d i, j d i, k d k, j .

Перша аксіома виконується внаслідок того, що d i, j 0 лише для випадку, коли кореляція повна ( 1). Друга аксіома виконується, оскільки

матриця коефіцієнтів крос-кореляцій і, відповідно, матриця відстаней D є симетричними за означенням. Третя аксіома виконується, оскільки вираз

~ ~

(2.11) еквівалентний Евклідовій відстані між двома векторами Gi та G j , отриманими із часових рядів Gi та G j , якщо інтерпретувати кожний запис

часового ряду як компоненту вектора. Отриманий вектор повинен мати одиничну норму, а саме, він має бути отриманий відніманням від кожного запису середнього значення для всього ряду та нормалізацією його стандартним відхиленням.

Тепер, зважаючи на наведені міркування, можна дати практичне визначення метричної відстані між валютними індексами (курсами) двох країн. Однак, метрична відстань є недостатньою для однозначного визначення таксономії (з математичної точки зору таксономією є деревоподібна структура класифікацій певного набору об’єктів).

Тому необхідно ввести більш обмежуючий топологічний простір, який буде однозначно асоційовано з таксономією. Таким обмежуючим топологічним простором є субдомінантний ультраметричний простір,

асоційований з матрицею Евклідових відстаней. Ультраметрична відстань визначається також трьома аксіомами. Перші дві співпадають з аксіомами метрики Евкліда, тоді як нерівність трикутника (iii) замінюється більш сильною нерівністю, яка називається ультраметричною нерівністю

В просторі елементів, де визначена метрика, завжди можна отримати субдомінантну ультраметрику. В ультраметричному просторі елементи розміщуються не вздовж однієї лінії, а на ієрархічному дереві. Набір індексів країн може інтерпретуватись як абстрактний простір, N елементів якого можуть бути з’єднані графом. У з’єднаному графі із взятими відстанями між усіма точками абстрактного простору мінімальне остівне дерево – МОД (minimal spanning tree – MST) має ( N 1) ребро і найменшу

44

довжину із довжин всіх остівних дерев, виходячи з суми відстаней між двома точками. Структура ієрархічного дерева отримується з матриці ультраметричних відстаней та МОД, асоційованого з нею.

Мінімальне остівне дерево та асоційоване з ним ієрархічне дерево показують існування кластерів будь-яких активів ринків, відомості про які мають значення з економічної точки зору. Отримана таксономія дозволяє групувати економічні об’єкти, що є гомогенними у сенсі економічної активності.

Розглянемо методику побудови мінімального остівного та асоційованого з ним ієрархічного дерева на прикладі системи індексів MSCI, яка включає 49 країн, з яких – 23 розвинених [74]. Для побудови мінімального остівного дерева, асоційованого з Евклідовою відстанню, необхідно виконати наступні дії [202].

Спочатку усі елементи матриці відстаней D розташовуються у порядку неспадання. Наприклад, маємо наступні вісім відстаней:

Spain-Italy d=0.61177

France-Italy d=0.64137

Nedherlands- d=0.6462

France

Germany- d=0.65383

France

France-Spain d=0.69175

Argentina- d=0.73039

Brazil

Switzerland- d=0.77672

Italy

Belgium- d=0.80568

France

Mexico- d=0.8217

Argentina

Мінімальне остівне дерево послідовно будується шляхом з’єднання усіх елементів у граф, виходячи із мінімальних відстаней між країнами на ринку.

Почнемо із пари елементів із найменшою відстанню. У даному випадку це дві країни: Spain та Italy (d=0.61177). Наступною найменшою за величиною відстанню є відстань між елементами France та Italy (d=0.64137), тому додаємо до МОД елемент France та з’єднуємо його з елементом Italy. Таким чином, отримане дерево вже буде мати вигляд France-Italy-Spain. Наступною парою елементів у відсортованому списку є країни Nedherlands- France, включаємо елемент Nedherlands до дерева. Аналогічно додаємо країну Germany. Наступною парою країн з найменшою відстанню є France-

45

Spain, проте обидві країни вже включено в мінімальне остівне дерево, тому для цієї пари нічого не робимо. Аналогічно продовжуємо процедуру, поки всі елементи не будуть включені в дерево.

Таким чином, у результаті перебору всіх відстаней отримаємо мінімальне остівне дерево, що буде характеризувати взятий фрагмент фінансового ринку стосовно того, які країни корелюють між собою тісніше, на скільки груп (кластерів) розподілений ринок і якого характеру цей розподіл тощо.

Якщо провести кластерний аналіз валютного ринку, то ми одержимо кластери груп країн, валютні ринки яких більш корельовано між собою: європейський кластер, азійсько-тихоокеанський, американський тощо. Кластерний аналіз можна проводити у вигляді динамічної процедури. При цьому аналіз продиться для вибраного часового вікна, вікно переміщується вздовж часового ряду, а процедура повторюється до тих пір, поки часовий ряд не вичерпано.

У роботі [295] із застосуванням кластерного аналізу ми провели порівняльне дослідження конкурентоспроможних кластерів в економіці України і США за даними фондових ринків.

Таким чином, ми одержали потужний інструмент для візуалізації кореляційних зв’язків між ринковоми агентами. У розділі 4 ми покажемо, що динамічний кластерний аналіз можна використати для дослідження кризових явищ.

Рис. 2.5. Мінімальне остівне (зліва) та ієрархічне (справа) дерева, побудовані для матриці індексів MSCI. Чітко виділяються європейський, азійський ринки, а також пари Канада-США і Австралія-Нова Зеландія

Аналіз структури складної системи шляхом побудови розглянутих вище графів має суб’єктивний характер, оскільки важко визначити зміни в

46

усій системі, розглядаючи лише її граф. Необхідно оперувати певними числовими характеристиками системи, по зміні яких можна робити висновок про стан системи [25]. Такими характеристиками можуть бути коефіцієнт кластеризації, діаметр графа, середня довжина шляху на графі [17]. Розглянемо докладніше ці коефіцієнти та спосіб їх обчислення.

Коефіцієнт кластеризації (транзитивності) графа

Існують різні способи визначення коефіцієнту кластеризації. Розглянемо деякі з них.

1) Візьмемо деяку вершину з графу та будемо обчислювати коефіцієнт кластеризації цієї вершини. До цієї вершини безпосередньо приєднані ki вершин. Між цими вузлами існує Еі ребер. Максимально можлива кількість ребер, при якій ці вершини утворюють кластер, дорівнює ki(ki+1)/2.

Коефіцієнт кластеризації вершини є відношенням кількості Ei ребер, які фактично існують між даними вершинами, до кількості ребер, при якому б ці вершини утворили кластер:

Будемо обчислювати коефіцієнт кластеризації елемента France. Безпосередньо з ним з’єднано 5 країн. Між 6 країнами максимально

47

2.2 Ентропійні методи дослідження фінансово-економічних систем

Уроботах по дослідженню критичних явищ, зокрема, в [161, 162], висловлюється та підтверджується гіпотеза про колективну зміну поведінки суб’єктів (елементів) систем, що й приводить до загальної зміни їх структури. Так, перед кризою в економічній системі починає спостерігатись спільний рух трейдерів в одному напрямку на великих масштабах, в той час як на малих спостерігаються хаотичні дії, що загалом приводить до зростання складності системи та її невизначеності. На основі такої гіпотези можна зробити висновок про ймовірність дослідження критичних явищ за допомогою методів, що дозволяють визначати характеристики складності та невизначеності систем. Однією з характеристик складності системи є ентропія.

Розглянемо сучасні підходи до використання ентропійних характеристик системи для вимірювання динамічних властивостей складних систем.

Утермодинаміці величина ентропії S є мірою кількості енергії у фізичній системі, яка не може бути використана для виконання роботи і є мірою безладдя, присутнього в системі. Поняття ентропії було вперше введено у 1865 році Рудольфом Клаузіусом [28]. Він визначив зміну ентропії термодинамічної системи для процесу, що характеризується властивістю

зворотності, як відношення зміни загальної кількості тепла Q до величини абсолютної температури T:

S Q /T .

Р. Клаузіус дав величині S назву „ентропія”, що походить від грецького слова τρoπή (зміна, перетворення). У 1877 р. Людвіг Больцман з’ясував, що ентропія системи може мати відношення до кількості можливих мікроскопічних станів („мікростанів”), що узгоджуються з їх термодинамічними властивостями [19]. Больцман постулював що,

S kB ln ,

де константу kB =1.38·10–23 Дж/К ми знаємо тепер як постійну Больцмана, а

Ω є кількістю мікростанів, які можливі в наявному макроскопічному стані. Цей постулат, відомий як принцип Больцмана, є витоком статистичної механіки, яка описує термодинамічні системи, використовуючи статистичну поведінку компонентів, із яких вони складаються. Принцип Больцмана пов’язує мікроскопічні властивості системи ( ) з однією з її термодинамічних властивостей ( S ).

50