4. Практическое применение программного комплекса в качестве системы поддержки принятия решений

Архитектура разработанной системы поддержки принятия решений была разобрана в предыдущей главе. Эта часть работы посвящена анализу работы системы.

1. Математические критерии оценки качества прогнозов

Для оценки качества прогнозов необходимо выделить ряд количественных и статистических критериев. Чамкина Елена в своей статье «Сравнение моделей временных рядов» предложила использовать следующий набор показателей [44]:

1. Модельная погрешность(модельный остаток):

,

(3.30)

где — фактическое значение показателя на -й момент времени;

— значение показателя, полученное с помощью модели на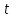 -й момент времени;

2. Абсолютная ошибка прогноза:

   (3.31)

3. Средняя абсолютная ошибка прогноза MAE(meanabsoluteerror):

,

(3.32)

где — число ретроспективных наблюдений.

4. Среднеквадратичное отклонение RMSE (root mean squared error):

(3.33)

Однако у этого способа есть несколько особенностей, например, большая чувствительность к большим отклонениям прогнозируемого значения от реального. Пусть построенная модель в целом довольно хорошо повторяет реальные данные о продажах, но имеются несколько точек, где отклонение от реальных данных большое. Рассчитывая для модели среднеквадратическую ошибку, в таком случае оценка качества модели может быть неудовлетворительной, и в результате принимается неправильное решение при выборе модели. Для устранения этого недостатка необходимо компенсировать величину ошибки значимостью этой ошибки. В таком случае возможность перевеса множества мелких ошибок одной крупной удастся избежать.

5. Средний процент ошибки MPE (mean percentage error):

(3.34)

MPE характеризует относительную степень смещённости прогноза. При условии, что потери при прогнозировании, связанные с завышением фактического будущего значения, уравновешиваются занижением, идеальный прогноз должен быть несмещенным, и обе меры должны стремиться к нулю. Средняя процентная ошибка не определена при нулевых данных и не должна превышать 5%.

6. Относительная ошибка прогноза:

   (3.35)

7. MAPE–meanabsolutepercentageerror,средний абсолютный процент ошибки(средняя относительная ошибка прогноза):

(3.36)

Отрицательные и положительные ошибки подавляют друг друга, поэтому для оценки качества построенной модели необходимо использовать среднюю абсолютную относительную ошибку.

8. Абсолютное отклонение от средней:

   (3.37)

9. Среднее абсолютное отклонение MAD(meanabsolutedeviation):

   (3.38)

10. —коэффициент детерминации. Характеризует степень сходства исходных данных и предсказанных. Не зависит от единиц измерения данных, поэтому поддается сравнению:

(3.39)

Если , это означает, что регрессия ничего не дает, т.е. знаниене улучшает предсказания дляпо сравнению с тривиальным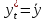. Другой крайний случайозначает точную подгонку: все точки наблюдений лежат на регрессионной прямой. Чем ближе к 1 значение, тем лучше качество подгонки.

11. Коэффициент несоответствия Тейла:

(3.40)

Индекс Тейла показывает степень схожести временных рядов и. Чем ближе он к нулю, тем ближе сравниваемые ряды.

Алгоритм вычисления критериев:

1. Вычислить модельную погрешность по формуле (3.30).

2. Вычислить абсолютную ошибку прогноза по формуле (3.31).

3. Вычислить среднюю абсолютную ошибку прогноза MAE по формуле (3.32).

4. Вычислить среднеквадратичное отклонение RMSE по формуле (3.33).

5. Вычислить относительную ошибку прогноза по формуле (3.35).

6. Вычислить среднюю относительную ошибку прогноза MAPE по формуле (3.36). Показатель MAPE, как правило, используется для сравнения точности прогнозов разнородных объектов прогнозирования, поскольку он характеризует относительную точность прогноза. Для прогнозов высокой точности 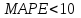, хорошей – (), удовлетворительной – (MAPE). Целесообразно пропускать значения ряда, для которых.

7. Вычислить абсолютное отклонение от средней по формуле (3.37).

8. Вычислить коэффициент детерминации по формуле (3.39).

9. Вычислить коэффициент несоответствия Тейла по формуле (3.40).

Из всех вычисленных показателей только средний абсолютный процент ошибки (MAPE), коэффициент детерминации () и коэффициент несоответствия Тейла () являются относительными и не зависят от абсолютных показателей анализируемых временных рядов. Поэтому, именно они были выбраны в качестве критериев оценки качества прогнозов.