Критерии согласия распределения Коши с распределением данных на виртуальном рынке по результатам 20 независимых экспериментов

Критерий	Количество экспериментов, подтвердивших гипотезу с уровнем значимости равным или меньше 5%
Кси квадрат (Пирсон)	16/20
Колмогоров	19 / 20
Критерий	Количество экспериментов, подтвердивших гипотезу
Романовский	20/20
Ястремский	20/20

Всего было проведено 20 экспериментов, в ходе которых параметры распределения Коши подстраивались под данные симуляции, а потом проводились расчёты критериев Пирсона, Колмогорова, Романовского и Ястремского. Результаты этих экспериментов представлены в таблице Таблица 3.7.

По результатам 20 экспериментов был сделан вывод, что , а из этого согласно формулам (3.14) и (3.25) следует, что

(3.26)

Иными словами, распределения реального и виртуального рынка совпадают. А это является одним из доказательств того, что процессы, происходящие на реальных рынках ценных бумаг и виртуальном рынке «FIMAS» имеют одинаковую природу.

4. Фрактальность рыночных процессов

Рынок ценных бумаг является сложной системой, процессы которого не могут быть описаны простыми линейными законами. Для нелинейных процессов Хёрст предложил вычислять экспонентукак наиболее важную характеристику. Логарифм отношения размаха (т.е. разность между максимальным и минимальными значениями временного ряда на некотором интервале) к среднему квадратичному отклонению, делённый на логарифм длительности временного интервала, является оценка.

Для её вычисления сначала надо подготовить исходный ряд. В рамках эксперимента было рассмотрено 5 вариантов такой подготовки:

, , , ,

(3.27)

где – исходный ряд, при .

В рамках этой исследовательской работы анализировались лишь варианты, использующие приращения (т.е. 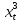,,), все из которых давали примерно одинаковые результаты.

После предварительной подготовки ряд делится наинтервалов:

(3.28)

После этого можно вычислять показатели ,и экспоненту Хёрста:

(3.29)

В зависимости от значения экспоненты Хёрста свойства процесса различают следующим образом:

При имеет место процесс случайных блужданий, который подтверждает гипотезу эффективного рынка.

При процесс имеет долговременную память и является персистентным, т.е. имеет положительную корреляцию для различных временных шкал.

При временной ряд является антиперсистентным с переключающимся время от времени средним значением.

Эксперимент

В ходе эксперимента были проанализированы 3 типа временных рядов: случайный ряд с равномерным распределением, данные с реального рынка ценных бумаг (NASDAQ) и данные с виртуального рынка в сценарии «FundamentalTradersExperiment.fmp». Для каждого типа проводилось от 10 до 30 экспериментов.

В рамках моих предыдущих работ на эту тему [81] была разработана специальная утилита, позволяющая рассчитывать экспоненту Хёрста для любого временного ряда. В таблице Таблица 3.8 приведены итоги расчётас помощью этой программы, а на рисунке Рис. 3.46 представлены примеры графиков экспоненты Хёрста в зависимости от разных значений.
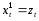