2. Критерий Колмогорова

Критерий согласия Колмогорова основан на другой мере близости распределений. Для оценки близости эмпирического распределения к теоретическому используется максимальная разница между накопленными эмпирическими и накопленными теоретическими частотами. Расчетное значение «лямбда-критерия» определяется по формуле:

(3.22)

где — максимальная разница между накопленными эмпирическими и теоретическими частотами,

— сумма всех эмпирических частот,

— количество интервалов,

— количество попаданий в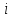-ый интервал эмпирического распределения,

— накопленная к-ому интервалу эмпирическая частота,

— накопленная к-ому интервалу теоретическая частота.

По рассчитанному значению 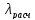по специальной таблице вероятностей «лямбда-критерия» определяется вероятность того, что рассматриваемое эмпирическое распределение подчиняется закону теоретического распределения.

3. Критерий Романовского

На основе ­ - критерия может быть рассчитан критерий Романовского:

(3.23)

где — количество интервалов,

— расчётное значение критерия.

В этой формуле число степеней свободы часто обозначают как . Эмпирическое и теоретическое распределения признаются близкими друг другу, если.

4. Критерий Ястремского

На основе ­ - критерия может быть рассчитан ещё один критерий согласия – критерий Ястремского:

(3.24)

где — расчётное значение критерия Пирсона,

— число групп,

, при.

В этой формуле число степеней свободы часто обозначают как . Эмпирическое и теоретическое распределения признаются близкими друг другу, если.

Результаты эксперимента

В приложениях Приложение 20-Error: Reference source not found представлены результаты сравнения двух теоретических распределений иcраспределением на реальном рынке.

– нормальное распределение при ,и мультипликаторе, вычисленное на интервалес шагом(32 интервала).

– распределение Коши при ,и мультипликаторе, вычисленное на интервалес шагом(32 интервала).

– распределение средней дневной цены акций компании «Юкос» за период с 25.05.2005 по 19.09.2006 (330 значений, 32 интервала).

Краткие результаты эксперимента можно посмотреть в таблице Таблица 3.3, полную версию расчётов – в приложениях Приложение 20-Error: Reference source not found.

Как видно, нормальное распределение, хоть по внешнему виду напоминает распределение реальных данных (Рис. 3.44), но по результатам эксперимента не удовлетворяет ни одному из критериев согласия.

Критерии согласия двух теоретических распределений с распределением приращения максимальной цены за день для акции компании «Юкос» за период с 25.05.2005 по 19.09.2006

Критерий	Теоретич. распред, сравниваемое с распределением реальных данных	Значение	Уровень знач.	Подтверждает гипотезу?
Кси квадрат (Пирсон)	Коши	8,783	0,003	Да
	Нормальное	43,364	0,99993	Нет
Колмогоров	Коши	0,542	0,001	Да
	Нормальное	2,015	1	Нет
Критерий	Теоретич. распред, сравниваемое с распределением реальных данных	Значение	Порог критерия	Подтверждает гипотезу?
Романовский	Коши	1,885	должен быть меньше 3	Да
	Нормальное	6,402		Нет
Ястремский	Коши	2,253		Да
	Нормальное	5,399		Нет

С другой стороны, распределение Коши удовлетворяет критерию Пирсона с уровнем значимости , критерию Колмогорова с уровнем значимости, а также критериям Романовского и Ястремского.

Всего было проведено 20 экспериментов, в ходе которых параметры теоретических распределений подстраивались под реальные данные, а потом проводились расчёты критериев Пирсона, Колмогорова, Романовского и Ястремского. Результаты этих экспериментов представлены в таблице Таблица 3.4.

Рис. 3.44. Плотность вероятности распределения Коши, нормального распределения и реальных данных