3. Сходство статистических характеристик изменения цен и объёма торгов

Чтобы иметь возможность правильно оценивать показатели виртуального рынка, в рамках диссертационного исследования был проведён анализ динамики технических показателей торгов на реальном рынке. В рамках него были рассмотрены изменение средней, максимальной и цены закрытия, а также объема торгов компаний РАО ЕЭС, ЮКОС и КАМАЗ за различные промежутки времени: от одного месяца до трёх лет.

Все три компании совершенно разные. Акции компании РАО ЕЭС вели себя достаточно стабильно за весь промежуток времени. Акции ЮКОСа и Камаза резко меняли свою цену на некоторых промежутках (приложения Приложение 8-Приложение 13). Такой выбор компаний в некоторой степени гарантировал, что обнаруженные закономерностями будут не просто случайными совпадениями.

Как и ожидалось, такие параметры как среднее, дисперсия, СКО и ковариация были совершенно разными у всех акций. Единственный статистический параметр, который был примерно одинаковый – это вид графика плотности распределения (рис. 3.40). Он имеет заметный пик, который может быть смещён к одному или другому краю. График плотности распределения выглядит примерно одинаково как для цен, так и для объемов торговли (рис. 3.41), именно поэтому на него будет обращено особое внимание в рамках данного исследования.

Рис. 3.40. График распределения средней, максимальной и цены закрытия акций компании «Юкос» за период с 25.05.2005 по 19.09.2006

Рис. 3.41. График распределения объема торгов акций «Камаз» за период с 19.02.2007 по 25.05.2007

Было отмечено, что график плотности распределения этих параметров мог быть смещён в ту или иную сторону; также могли отличаться размер пика и толщина хвостов. В связи с этим, выдвинута гипотеза о том, что процессы, происходящие на виртуальном и реальных рынках могут быть описаны одним и тем же законом распределения , параметры которого отличаются в зависимости от условий эксперимента (конкретной конъюнктуры рынка).

Если доказать, что распределение на реальном рынке ценных бумаг соответствуети распределение на виртуальном рынке ценных бумагсоответствует, то можно с уверенностью утверждать, чтосоответствует. Это, в свою очередь, будет свидетельствовать о том, что процессы, происходящие на реальных рынках ценных бумаг и виртуальном рынке «FIMAS» имеют одинаковую природу.

(3.14)

Чтобы найти этот закон распределения , было рассмотрено 12 различных типов распределений, из которых 10 были сразу отброшены по причине непохожей формы. Для окончательного сравнения были взяты два распределения: нормальное распределение Гауса и распределение Коши.

Нормальное распределение, также называемое распределением Гаусса, — распределение вероятностей, которое играет важнейшую роль во многих областях знаний. Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть является с математической точки зрения не одним распределением, а целым их семейством. Значения параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения).

Стандартнымнормальным распределением называется нормальное распределение с математическим ожиданием 0 и дисперсией 1.

Рис. 3.42. Плотность вероятности нормального распределения

Плотность вероятности нормального распределения имеет следующий вид (Рис. 3.42):

,

(3.15)

где- математическое ожидание,

- дисперсия.

Функция распределения для него имеет следующий вид:

,

(3.16)

где - математическое ожидание,

- дисперсия.

Распределение Кошизадаётсяплотностью, имеющей вид:

,

(3.17)

где — параметр сдвига;

γ > 0 — параметр масштаба.

Если x₀= 0 и γ = 1, то такое распределение называетсястандартнымраспределением Коши. Стандартное распределение Коши является частным случаем распределения Стьюдента:

(3.18)

Рис. 3.43. Плотность вероятности распределения Коши

Случайная величина, имеющая распределение Коши, является стандартным примером величины, не имеющей математического ожидания и дисперсии. Функция распределения Коши имеет вид (Рис. 3.43):

,

(3.19)

где — параметр сдвига;

γ > 0 — параметр масштаба.

Реальные данные– это цены акций различных российских и зарубежных компаний за периоды от трёх месяцев до десяти лет.

Распределение реальных данных (а также любое другое распределение котировок акций и объёма торгов в рамках этой диссертационной работы) вычислялось по следующей методологии:

Для исходного ряда размером вэлементов надо создать новый ряд размеромэлементов. Тогда значения конечного ряда будут рассчитываться по формуле

(3.20)

где – конечный ряд,.

После этого надо найти распределение получившегося ряда стандартным способом.

В данном случае к конечному распределению был применён понижающих коэффициент , чтобы искусственно уменьшить количество данных в исходной выборке, приведя сумму частот максимально близко к сумме частот теоретических распределений. Для этих же целей использовались мультипликаторы для теоретических распределений.

Методика расчёта статистических критериев согласия

1. Критерий Пирсона, или критерий— наиболее часто употребляемый критерий для проверки гипотезы о законе распределения. Обозначим через X исследуемую случайную величину. Пусть требуется проверить гипотезуо том, что эта случайная величина подчиняется закону распределения. Для проверки гипотезы произведём выборку, состоящую изнезависимых наблюдений над случайной величиной.

Для проверки критерия вводится статистика:

(3.21)

где — количество интервалов,

— количество попаданий вi-ый интервал теоретического распределения,

— количество попаданий вi-ый интервал эмпирического распределения.

Эта величина в свою очередь является случайной (в силу случайности X) и должна подчиняться распределению . Чем меньше эмпирические и теоретические частоты в отдельных группах отличаются друг от друга, тем меньше эмпирическое распределение отличается от теоретического, то есть тем в большей степени эмпирическое и теоретическое распределения согласуются между собой.

Для оценки существенности расчетной величины «хи-квадрат» оно сравнивается с табличным (критическим) значением, определяемым по статистическим таблицам значенийопределяют в зависимости от уровня значимостии параметра, где— вероятность ошибки,— число оцененных параметров теоретического распределения по наблюдаемым значениям признака.

Если 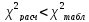, то считают, что распределения близки друг другу, различия между ними несущественны.

Для более точного расчёта уровня значимости в рамках данного исследования была использована статистическая функция«ХИ2ТЕСТ»(«CHITEST»)из программного продуктаMicrosoftExcel2007.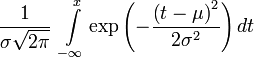