Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Запорожская Государственная Инженерная Академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

АКР1 по МЭС / zuiev

.pdf

Скачиваний:

Добавлен:

27.05.2015

Размер:

419.17 Кб

Скачать

☆

Зуев В. А., Горыня Л. М. Переходные процессы в МДП-системах

▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬

УДК 621.315.592

Зуев В. А., д.ф.-м.н.; Горыня Л. М., к. ф.-м.н.

(Государственный университет информационно-коммуникационных технологий)

ПЕРЕХОДНЫЕ ПРОЦЕССЫ В МДП-СИСТЕМАХ

Зуєв В. О., Гориня Л. М. Перехідні процеси в МДН-системах. Теоретично вивчений малосигнальний ефект поля. Прийнята до уваги модуляція провідності області приповерхневого просторового заряду. Теорія перехідних процесів в МДН-структурах може бути використана для аналізу телекомунікаційних детекторів, включаючи фотодетектори в системах оптичного зв’язку.

Ключові слова: МДН-СИСТЕМА, МОДУЛЯЦІЯ ПРОВІДНОСТІ, ЕФЕКТ ПОЛЯ, ПРИПОВЕРХНЕВИЙ ПРОСТОРОВИЙ ЗАРЯД

Зуев В. А., Горыня Л. М. Переходные процессы в МДП-системах. Теоретически изучен малосигнальний эффект поля. Принята во внимание модуляция проводимости области приповерхностного пространственного заряда. Теория переходных процессов в МДП-структурах может быть использована для анализа телекоммуникационных детекторов, включая фотодетекторы в системах оптической связи.

Ключевые слова: МДП-СИСТЕМА, МОДУЛЯЦИЯ ПРОВОДИМОСТИ , ЭФФЕКТ ПОЛЯ , ПРИПОВЕРХНОСТНЫЙ ПРОСТРАНСТВЕННЫЙ ЗАРЯД

Zuiev V. O., Gorynia L. M. Transition processes in MOS-structures. Small signal field-effect was theoretically studied. It was takes into account the conductivity modulation at the surface space charge region. The theory of the transition processes in MOSstructures may be used for analysis of telecommunication detectors including optical communication system photodetectors.

Key words: MOS-SYSTEM, ACCOUNT CONDUCTIVITY, FIELDEFFECT, SURFACE SPACE CHARGE

Введение. Как известно, системы металл-диэлектрик-полупроводник (МДП) наиболее перспективны для использования в электронных системах связи, в частности в качестве приемников оптической информации. Речь идет о приборах с зарядовой связью и об МДПтранзисторах и фототранзисторах. Поскольку оптическая информация поступает по волоконным световодам обычно в виде световых импульсов, принципиальным является анализ переходных процессов в фотоприемниках.

В МДП-системах управление приповерхностной областью происходит обычно путем подачи синусоидального или импульсного электрического поля. Указанное поле позволяет управлять электропроводностью приповерхностной области (так называемый эффект поля). Ранее кинетика эффекта поля рассматривалась без учета модуляции проводимости непосредственно в области приповерхностного пространственного заряда. В настоящей работе рассматривается такая модуляция.

1. Анализ кинетики эффекта поля с учетом модуляции проводимости в области приповерхностного пространственного заряда

1.1. Граничные условия. Рассмотрим поверхностные электронные состояния (ПЭС) с концентрацией Nt , см-2, сечениями захвата электронов и дырок Cnt , Cpt , см-2, энергетическим положением Et , kT , отсчитанным от середины запрещенной зоны на поверхности. Изменение во времени концентрации электронов, захваченных на ПЭС ((nt ), описывается следующим уравнением:

dnt	v cnt (pt ns nt p1t ) cpt (nt ps pt n1t ) .	(1)
dt

Члены в правой части (1) описывают захват и выброс электронов из ПЭС, а также захват и выброс дырок с тепловой скоростью v. Индекс s относится к величинам, взятым на геометрической поверхности полупроводника. Величины n1t , p1t соответствуют поверхностным концентрациям электронов и дырок при совпадении уровня Ферми на

поверхности полупроводника us с t и описываются формулой	n1t, p1t ni	exp( t ) ,
где ni –концентрация носителей заряда в собственном материале.

Вісник ДУІКТ. – 2012. – Т.10, №2. – Стор. 36

Зуев В. А., Горыня Л. М. Переходные процессы в МДП-системах

Отметим, что связь us

с положением уровня Ферми в объеме

и изгибом зон ys

определяется как

us ub ys .

Для напряженности поля на поверхности согласно теореме Остроградского-Гаусса имеем:

(суммирование по числу ПЭС)

(2)

П 0kT

В линейном режиме ( ps ps ;

ns ns ;

1) при воздействии на полупроводник

света или электрического поля с частотой

(в

направлении,

перпендикулярном

поверхности) имеем из (1)

d nt

r n

) n r p

(3)

где

v cnt Nt fpt и

– скорости захвата электронов и дырок на ПЭС;

rnt

rpt

v cpt Nt

fnt

v c

v c n

f 1

– обратные времена выброса электронов и

дырок из ПЭС;

fnt

fpt

– равновесные функции заполнения уровней электронами и

дырками:

fnt

1 fpt

1 exp( t us

ys).

Для

поверхностных

потоков

носителей

из

(3)

имеем:

jns snp ps

snn ns ,

jps

spp ps

spn ns , где snp,

snn,

spp,

spn,

– коэффициенты мономолекулярной поверхностной

рекомбинации: snp

gntrpt

;

snn

(gpt

i )rnt

; spp

(gnt

i )rpt

;

spn

gptrnt

gt i

Для добавочного электрического поля при возбуждении светом на поверхности в

линейном

режиме из

(2)

получаем:

d y

( n

где

n –

концентрация

равновесных

носителей

квазинейтральном

объеме;

kT /(2e2n )

–

длина

экранирования; коэффициенты

связаны

со

скоростями

захвата

носителей и

обратными временами их выброса соотношениями

;

rpt

При возбуждении неравновесных носителей заряда синусоидально-модулированным поперечным электрическим полем с амплитудой Qs имеем:

d y

(

) Q .

2l2n

Распределение неосновных носителей в области пространственного заряда (ОПЗ)

определяется

как p1(x) ps exp(ys y) pv exp( y)[ ys y(x)]

[1]; распределение в

объеме – p

(x) C exp

exp

, где L

– длина диффузии.

LД

1.2. Неравновесный эффект поля.

При синусоидальной модуляции поля для

подвижности эффекта поля

имеем следующую связь между изменением проводимости

и величиной Q :

или

eП

skT

d y

(1 b) p1dx p1dx b

eП

4 l

(4)

Вісник ДУІКТ. – 2012. – Т.10, №2. – Стор. 37

Зуев В. А., Горыня Л. М. Переходные процессы в МДП-системах

ey1 1

e y1 1

Далее: y ys

nse

dy1

pse

dy1

ps , где

F3(y )

F(y) ey y 1 e 2uB(e y 1) . Далее, согласно [1] имеем:

ey0s

) p

2(u

)

spne

i LpL

y0s

2(uB y0s )

sppe

(1 e

(ys)) i LpL (1 f1 f2Ns)

ne y0s p Qs

d y

(5)

(6)

pe ys l

; l

Lsc

e y0s

y0s

знак

" "

где

;

n l

(ey0s y 0s

y0s

знак

" "

Lsc

1 L

e y2

Для функции f1,2

имеем:

f1,2

dy2dy1

. Используя (4), получаем:

2 Lp

F(y2)

eП

(y i ) bB( ) (1 b)A( )

(7)

(i k 1)(i g1)

где A( ) (l d ) 1 L0p

D d

L (1 f1)(Spn

e 2uB

ys ) d(Spn i L0pL f2e ys ) L0pL f2e 2ys

Dpd

2ys

Dpd

2uB ys

(Spp

) LpL f2e

(Spp

) de

Sppe

i LpL (1 f1)

;

Dpd

B( ) (d ) 1 i L0

L (1 f f

e ys ) S

E ys

(1 e uB ys ) ;

L0p

d(1 e

2uB ys ) 2L0

L (1 f f

e ys ).

Времена k

и g

описывают биекспоненциальную релаксацию эффекта поля. Запишем

их комбинацию

(8);

gn(1 e

2uB

)

(9),

k g

rp rn

		r e ys
где	r	p	;	r
где	r	d	;	r
	p	d		n

Из формулы (7) следует:

rn ; l

Re eП

Jm eП

2uB

d(1

) LpL

(1 f1

)( 1 1

) ( 1

k g

;

( 2 k 2)( 2 g 2)

2(ys)( k 1 g1 2) 2(ys ) ( k1 g1)

( 2 k 2)( 2 g 2)

	p
	p	f2e 2ys ) .
r		f2e 2ys ) .
r
	n

Вісник ДУІКТ. – 2012. – Т.10, №2. – Стор. 38

Зуев В. А., Горыня Л. М. Переходные процессы в МДП-системах

где

1(ys ) (1 b)ReA bReB ;

2(ys) (1 b)JmA bJmB ;

(1 f1)e

s ;

S – скорость поверхностной рекомбинации;

ReA g(S

)LpL

s f2e

JmA gv LpL (1 f1)

s S

(LpL e

) LpL

s ;

ReB gl 2gL

L (1 f

eys

) (1 e 2uB ys ) S

(1 2g

)

JmB gl v gLpL (1 f1

f2eys )

(1 e 2uB ys )(1 g v) .

1.3. Частные случаи.

а) Инверсия. В этом случае

L (1 f

) l

;

L f

eys

e ys ;

l L

uB .

В результате имеем:

3ys

;

ReA g(S

)L e 2

S(1

)

JmA gvL e ys

e 2uB ys (1 euB

)

(de uB L

) ;

1 3

ReB g(S

)L e

3ys

v2g2L e

uB (L e ys de 2uB ys );

JmB gve

gL e

(1 g

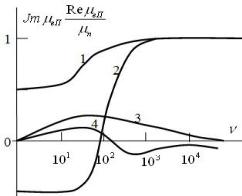
На рис.1 построены зависимости Re eП и
Jm eП	от частоты поля (кривые 2 и 3 – для
случая инверсии, кривые 1 и 4 – для случая
истощения, см. ниже).
Смена знака Re eП связана с тем фактом,
что при низких и высоких частотах модуляции
поля	имеет место влияние неравновесных

носителей различных знаков.

При нулевых частотах имеем:

eП (0)

g(S

) k ge

2ys

Рис. 1.Зависимости

б) Истощение. Для тангенса фазового сдвига имеем:

vy R1

( g2v2) R2

R2( g2v2) v2g2 R2

где

d L

L ;

S v2g(d L

L ).

Re eП и Jm eП

(10)

Вісник ДУІКТ. – 2012. – Т.10, №2. – Стор. 39

Зуев В. А., Горыня Л. М. Переходные процессы в МДП-системах

При частотах >102 числитель и знаменатель в (10) равны, соответственно,

g2v3deф

g3v4deф , т. е.,

tg v 1 .

В области изгибов зон

при r r

из (5) и (6) получим

r exp(2u

)

(11);

rp exp( ys )

(12).

l 1

dexp(2uB)

Время

(11)

соответствуют

биполярным

процессам

эффекте

поля,

а (12)

–

монополярным процессам.

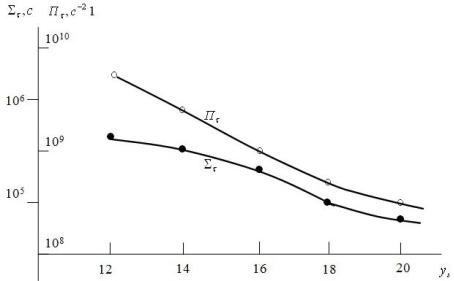
На рис. 2 пред-

ставлена

зависимость

комбинации

обратных

времен

биэкспонен-

циальной

релаксации

эффекта поля от изгиба

зон для общего случая,

т. е., изображены фор-

мулы (8) и (9).

Расчет

переходных

процессов

позволяет

анализировать

работу

устройств считывания в

электронных

системах

связи в

частности

Рис. 2. Зависимости обратных времен от изгиба зон

фотоприемных

устрой-

ствах

инфракрасного

диапазона [2,3].

Выводы. Проведен расчет переходных характеристик МДП-структур в эффекте поля. Расчет применим также для анализа фотопроводимости. Особенностью расчета является впервые проведенный учет модуляции проводимости в области приповерхностного пространственного заряда. Расчет применим для анализа работы систем считывания в электронных системах связи в частности в фотоприемных устройствах для современных оптических линий связи.

Литература

1.Зуев В. А. Неравновесные приповерхностные процессы в полупроводниках и полупроводниковых приборах / В. А. Зуев, А. В. Саченко, К. Б. Толпыго. – М.: Сов. радио.- 1977. – 256 с.

2.Reine M. B. HgCdTe Photodiodes for IR detection / M. B. Reine // Proc. SPIE. – 2001. – 4248. – P. 266-277.

3. Шумовые характеристики ИК	фотоприемного устройства / [А. Г. Голиков,
В. В. Забудский, В. А. Волошин и др.] //	Оптоэлектроника и полупроводниковая техника. –
2003. –Т.38. – С.118-126.

Вісник ДУІКТ. – 2012. – Т.10, №2. – Стор. 40

Соседние файлы в папке АКР1 по МЭС

#
27.05.201585 б14Bipolar Junction Transistors.URL
#
27.05.2015918.99 Кб20foep_manual_2.pdf
#
27.05.2015623.99 Кб15L_5.pdf
#
27.05.2015283.44 Кб21str8-11.pdf
#
27.05.20152.53 Mб14StudentBank.ru_39055.rtf
#
27.05.2015419.17 Кб13zuiev.pdf
#
27.05.201511.84 Mб14аппрок5сим.rtf
#
27.05.20151.25 Mб100Аппроксимация интерполяция экстраполяция.pdf
#
27.05.201583 б15АППРОКСИМАЦИЯ НЕЛИНЕЙНЫХ ХАРАКТЕРИСТИК ЭЛЕКТРОННЫХ КОМПОНЕНТОВ СПЛАЙН-ФУНКЦИЯМИ.URL
#
27.05.2015102 б13Модель Гуммеля-Пуна.URL
#
27.05.201595.74 Кб28Подавление эффекта Миллера в схемах управления MOSFET.doc