6. Расчет токов биполярного транзистора

Основные допущения идеализированной теории биполярных транзисторов

Для построения идеализированной модели биполярного транзистора будем считать, что его структура разбивается на области пространственного заряда (обедненные области эмиттерного и коллекторного переходов) и квазинейтральные области эмиттера, базы и коллектора, в которых выполняется условие  n  p. Кроме того, примем обычные допущения идеализированной теории n-p-перехода:

1. Области пространственного заряда практически не содержат подвижных носителей заряда и имеют резкие границы с квазинейтральными областями эмиттера, базы и коллектора.

2. Объемные сопротивления эмиттера, базы и коллектора близки к нулю и внешние напряжения приложены непосредственно к эмиттерному и коллекторному переходам.

3. На краях областей пространственного заряда (на границах переходов) справедливы граничные уравнения, связывающие концентрации носителей заряда с напряжениями, приложенными к переходам.

4. В областях эмиттера, базы и коллектора имеет место низкий уровень инжекции неосновных носителей заряда.

Составляющие токов транзистора

Рассмотрим транзистор, включенный по схеме с ОБ (рис.9). Во внешних цепях транзистора будут протекать токи i_Э, i_К, i_Б. За положительные направления токов примем указанные стрелками (они совпадают с физическими направлениями токов в активном режиме). Внешние напряжения u_ЭБ и u_КБ , как и ранее, будем отсчитывать от общего электрода (в данном случае - базы).

Кроме того, введем напряжения на переходах транзистора u_ЭП - на эмиттерном переходе, u_{КП -} на коллекторном. Эти напряжения будем считать положительными, если они прямые ( “+” приложен к p- области, а “-” к n-области) и отрицательными, если они обратные.

Для рассматриваемого n-p-n-транзистора в схеме с ОБ

u_ЭП= - u_ЭБ = u_БЭ и u_КП = - u_КБ .

Для p-n-p-транзисторов: u_ЭП= u_ЭБ , u_КП = u_КБ Использование понятий напряжений на переходах позволяет получить одинаковые формулы для n-p-n- и p-n-p-транзисторов. Как было показано в предыдущей главе, каждый ток содержит различные составляющие; для удобства сгруппируем их следующим образом:

1. Выделим единственную полезную составляющую, обусловленную переносом электронов из эмиттера в коллектор. Назовем ее током связи i_Э-Кк ( направление тока на рис.9 обратно направлению движения электронов).

2. Дырочные токи переходов и токи, обусловленные рекомбинацией в базе, объединим в дополнительные токи эмиттерного i _эд и коллекторного i _кд переходов. Эти токи замыкаются каждый через свой переход и не могут передаваться из эмиттера в коллектор. Таким образом, наличие дополнительных токов приводит только к потерям энергии.

Полные токи транзистора могут быть представлены в виде:

(3.1)

Вредные дополнительные токи переходов мало изменяют токи i_Э и i_К ( на 1 - 3 %), однако именно они определяют ток базы.

Перенос электронов из эмиттера в коллектор. Ток связи

Расчет полезной электронной составляющей токов транзистора - тока связи i_Э-К - проведем, пренебрегая малыми дополнительными токами. С физической точки зрения это соответствует отсутствию рекомбинации в базе и переходах транзистора. Электронный поток из эмиттера в коллектор одинаков в любом сечении транзистора, а его величина зависит от процессов в базовой области ( в эмиттере и коллекторе электроны являются основными носителями, их концентрация велика и движение обеспечивается пренебрежимо малыми электрическими полями).

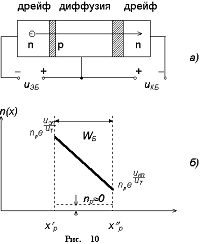
Перемещение электронов в базовой области (для нее электроны - неосновные носители) происходит путем диффузии за счет разной концентрации на границах базы с эмиттерным и коллекторным переходами, см. рис.10, ( для определенности будем полагать, что на обоих переходах действуют прямые напряжения u_ЭП >u_КП >0. Естественно, что дальнейшие рассуждения справедливы при произвольных напряжениях на переходах).

Вычисление тока связи будем проводить в произвольном сечении базы в следующей последовательности:

1. Найдем общее решение уравнения диффузии для электронов в базе.

2. Найдем граничные концентрации n(x_p) и n(x_p).

3. Получим распределение n(x) концентрации электронов и определим градиент концентрации

Определим величину диффузионного тока в базовой области, равного току связи. В соответствии с граничным уравнением p-n-перехода получим:

(3.2)

где n_p- равновесная концентрация электронов в p-базе. Запишем стационарное уравнение диффузии для электронов:

(3.3)

Если пренебречь рекомбинацией в базе (это эквивалентно условиюL_n   ), то уравнение (3.3) упрощается и приобретает вид:

или(3.4)

Таким образом, решением уравнения будет прямая линия, проходящая через точки n(x _p) и n(x_p ). Распределение электронов в p-базе показано на рис 10, из которого с учетом (3.2) следует:

Тогда ток связи может быть рассчитан по формуле:

,

где S - площадь переходов транзистора. Окончательно:

(3.5)

где (3.6).

Ток I₀ называется током насыщения транзистора. Он аналогичен электронной составляющей теплового тока изолированного p-n-перехода.

Часто ток связи представляют в виде разности нормальной i_N и инверсной i_I составляющих.

, (3.7)

где (3.8);

(3.9).

Физически i_N - это ток связи при u_КП = 0 , а i_I - ток связи при u_ЭП = 0. Таким образом, ток связи имеет две составляющие, каждая из которых зависит от напряжения на одном из переходов.

Дополнительные токи переходов

Дополнительные токи переходов складываются из дырочных и рекомбинационных составляющих (см. рис.11). В каждом переходе транзистора, помимо электронных, протекают и дырочные составляющие токов, обусловленные инжекцией дырок - основных носителей заряда в p-базе. Так как концентрация примеси в базе мала N_АБ<<N_DЭ , эти токи в десятки и более раз меньше электронных. Они могут быть рассчитаны по формулам:

(3.10)

где p_nЭ и p_nК - равновесные концентрации дырок в эмиттере и коллекторе соответственно. Рекомбинационные токи i' _рек и i' ' _рек обусловлены частичной рекомбинацией электронов, диффундирующих из эмиттера в коллектор. Скорость рекомбинации в базе (и рекомбинационные токи) пропорциональны избыточному числу неосновных носителей во всей базовой области (площадь под распределением  n(x) на рис.10.  n(x) = n(x)- n_p ), или

. (3.11)

Учитывая , что распределение  n(x) - линейно, по формуле трапеции получим:

, (3.12)

где ; (3.13)

. (3.14)

Ток i' _рек(u_ЭП) определяется рекомбинацией электронов, соответствующих нормальной составляющей тока связи i_N, а i'' _рек(u_КП) - инверсной i_I. Дополнительные токи каждого перехода складываются из рекомбинационных и дырочных составляющих:

и зависят каждый от напряжения на своем переходе.

Влияние обратного напряжения на коллекторном переходе на токи транзистора. Эффект Эрли

В соответствии с формулами 3.5 ...3.8 ток связи перестает зависеть от обратных напряжений при | u_КП| >> u_Т = 26 мВ. Однако реально такая зависимость существует, так как при увеличении обратных напряжений ширина n-p- переходов увеличивается, а ширина базы уменьшается. Зависимость ширины базы от величины обратного напряжения на коллекторе называется эффектом модуляции ширины базы или эффектом Эрли. (Аналогичный эффект в эмиттерном переходе интереса не представляет, так как на эмиттерный переход не подают больших обратных напряжений). На рис.12 показаны два распределения n(x) электронов в базе при двух значениях обратного напряжения на коллекторном переходе. Видно, что при u_КП = u_КП2 ширина базы уменьшилась на величину  W_Б. При этом увеличился градиент концентрации электронов

и, следовательно, увеличился и ток связи, являющийся диффузионным. Как следует из рис.12, большему обратному напряжению u_КП2 соответствует больший ток связи i_Э-К а, следовательно, и большие токи i_Э и i_К. Однако данный эффект в сотни раз слабее, чем влияние прямых напряжений на переходах, и часто не учитывается, или учитывается приближенно. Для учета эффекта Эрли уточняют формулу (3.6) теплового тока транзистора I ₀, принимая:

(3.16)

где I₀ - ток, определенный без учета эффекта Эрли по формуле (3.6), u_А - напряжение Эрли - параметр транзистора, характеризующий величину эффекта Эрли. Обычно u_А составляет десятки вольт и более.

Коэффициенты передачи токов

Полезный эффект в транзисторе создается за счет передачи эмиттерного тока из эмиттера в коллектор. Количественно эффективность этого процесса оценивают с помощью статического коэффициента передачи тока эмиттера  . Введем: при u_КП = 0. Смысл условия u_КП= 0 заключается в том, что при этом дополнительный ток коллекторного перехода i_КД = 0, и в коллекторной цепи течет только нормальная составляющая i_N полезного электронного тока. Тогда: . .Аналогично можно ввести и инверсный коэффициент передачи тока  _I , или

.

Отсюда следует:  i_N +  i_ЭД = i_N и  _I i_I +  _I i_КД = i_I , тогда

, (3.17)

, (3.18)

где:

и - статические коэффициенты передачи тока базы, прямой и инверсный соответственно. С учетом (3.17) и (3.18) формулы (3.1) удобно представить в виде:

;

;

.

В рассматриваемой упрощенной теории коэффициенты  ,  _I ,  ,  _I считаются постоянными, однако опыт показывает, что они изменяются, как при изменении тока связи i_Э-К ( на практике рассматривают зависимость от тока эмиттера i_Э, отличающегося от тока связи на несколько процентов, но легко измеряемого), так и от обратного напряжения на коллекторном переходе u_КП. Типичный вид зависимостей для  показан на рис.13 а,б. (Коэффициент  изменяется аналогично, но его изменениями можно пренебречь, так как   1. Пример: если  =0,99, то  =  /(1-  ) =99 , а при  =0,98  =49. Таким образом, изменению  на 1% соответствует изменение  примерно в 2 раза). В области малых токов эмиттера (рис.13а, участок 1) спад  связан с рекомбинацией носителей в самом эмиттерном переходе; в области больших токов (участок 3) уменьшение  связано с увеличением концентрации дырок в базе и возрастанием дырочной составляющей тока эмиттерного перехода. Возрастание  с увеличением обратного напряжения на коллекторе вызвано уменьшением ширины базы и рекомбинационных составляющих токов.