Х2 х2
Х1
а)
Х1
в) Х4
Х2
Х1
б) Х3
Х3
Рис.2.5 Таблица карты Карно: а) для двух аргументов; б) для трех аргументов; в) для четырех аргументов
Каждая клетка соответствует определенному набору аргументов, причем этот набор определяется присвоением значения 1 аргументам, на пересечении строк и столбцов которых расположена клетка.
Число клеток карты равно числу возможных наборов значений аргументов и при числе аргументов n равно 2n. В каждую клетку карты записывается значение функции для соответствующего этой клетке набора значений аргументов. Например, если функция задана таблицей истинности (см. таблицу 2.2), то в форме карты Карно эта функция будет представлена так, как показано на
рис. 2.6, а.
Таблица 2.2 - Таблица истинности функции F(x1x2x3)
-
Х1
0
0
0
0
1
1
1
1
Х2
0
0
1
1
0
0
1
1
Х3
0
1
0
1
0
1
0
1
F(x1x2x3)
0
1
0
1
0
0
1
1
При этом клетки верхней строки соответствуют следующим наборам (см. рис.2.6.а):
первая
клетка: х1=1;
х2=1;
вторая клетка: х1=1; х2=1; х3=1,
третья
клетка:
;х2=1;
х3=1,
четвертая
клетка:
,
,х3=1.
При записи функции в минимальной форме по картам Карно используются следующие правила.
Все клетки, содержащие 1, объединяются в замкнутые области. При этом каждая область должна представлять собой прямоугольник с числом клеток 2k, где k=0, 1, 2, 3, 4, ... . Области могут пересекаться, и одни и те же клетки могут входить в разные области. Затем производится запись минимального выражения в дизъюнктивной нормальной форме ДНФ. Каждая область в такой записи представляется членом, число аргументов в котором на k меньше общего числа аргументов функции п, (равно п—k). Каждый член МДНФ составляется лишь из тех аргументов, которые для соответствующей области имеют значения либо без инверсий, либо только с инверсией.
Х2
Х2
1 1 1 1 1 1 1
1
а)
I
1
1
Х1
Х1
1
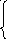
Х4
1
II
Х3
IV
б)
III
Х3
Рис.2.6 - Карта Карно: а) для функции F(x1x2x3) - для трех аргументов;
б) для функции F(x1x2x3) - для четырех аргументов
Таким образом, при охвате клеток карты замкнутыми областями следует
стремиться, чтобы число областей было минимальным, так как при этом будет минимальным число членов в ДНФ, а каждая область содержала возможно большее число клеток, поскольку при этом число аргументов в
членах будет минимальным. Так, для функции трех аргументов, представленной на рис. 2.6, а, клетки, содержащие 1, охватываются двумя областями. В каждой области две клетки, и так как 2k = 2, то, следовательно,
k
=
1. Поэтому для этих областей n-k=3-1=2.
В результате в ДНФ будет два члена и в
каждом из
них по два аргумента. Первой области
соответствует импликанта
х1х2,
а
второй области — импликанта
.
Следовательно,
минимальная ДНФ для этой функции будет:
Примером
задания функции четырех аргументов с
помощью карты Карно может служить карта,
приведенная на рис.2.6.б,
где выделены четыре области. Первая и
четвертая области имеют по две клетки;
для них n—k=3 и соответствующие им члены
будут
и
.
Области
II и III содержат по четыре клетки, и в ДНФ
они будут выражены членами, содержащими
по два аргумента
и
.Таким
образом, минимальная форма функции
будет
При построении замкнутых областей допускается сворачивание карты в цилиндр как по горизонтальной, так и по вертикальной оси с объединением противоположных граней карты.
Представление функции и минимизация ее с помощью карт Карно усложняется, если число аргументов больше четырех. Так, для представления функции пяти аргументов необходимо использовать две карты, каждая из которых представляет собой карту четырех переменных; одна для х5=1, а другая для х5=0. Эти карты располагаются одна над другой, и области охвата клеток могут быть трехмерными, т. е. в одну область могут входить клетки двух карт. Для минимизации функций с числом аргументов более 7—8 карты Карно практически не используются, и в этих случаях используются алгебраические методы, такие как метод Квайна, метод неопределенных коэффициентов и др.
При построении логических схем в качестве базисных функций кроме дизъюнкции, конъюнкции и отрицания могут быть использованы и другие функции, образующие полную систему. В этом случае минимальные формы могут быть получены переходом от базиса «дизъюнкция, конъюнкция и инверсия» к новому базису путем соответствующих преобразований. Например, при переходе к базису в виде функции Шеффера используются инверсия и формулы Моргана.