Zadania

Задачи

1. Показать, что имеет место

∂x ∂ y ∂ z 1

∂y ∂ z ∂ x =−

2.Показать, что имеет место

∂∂ xz y=1∂ z ∂ x y

CP−CV = ∂∂VT P[P ∂∂VE T ]=− ∂∂TP V [P ∂∂VP T ∂∂ EP T ]

5.Получить соотношение

CV =C P ∂∂ VT 2P ∂∂ Vp −T1

7. Найти адиабатическую сжимаемость идеального газа при квазистатическом адиабатическом сжатии. Скорость звука определяется соотношением

c= ∂ p (ρ - плотность). Считая что дифференцирование производится при

∂ ад

адиабатическом изменении, вычислить скорость звука в воздухе при 1 атм 0о С и найти ее зависимость от температуры.

8. Газ подчиняется уравнению Дитеричи

где n – число молей, а, b – постоянные, характеризующие вещество. Показать, что в критической точке

и записать уравнение состояния в универсальной форме закона соответственных состояний

9. Вычислить КПД цикла Дизеля полагая, что CP, CV – const. Доказать, что

10.Идеальный газ расширяется из объема V1 в вакуум до объема V2. Определить возрастание энтропии.

11.Записать уравнение состояние идеального стержня и построить изотермы.

12.Для идеального стержня получить соотношение

где l- длина стержня, α - коэффициент температурного расширения, σ- площадь поперечного сечения, EЮ – модуль Юнга, S – энтропия, Т – температура.

13. Показать, что для газа, давление которого при постоянном V изменяется пропорционально Т, энтропия возрастает с увеличением V. ( P= f V T )

14.Доказать, что свободное адиабатическое расширение от V до V+dV является необратимым процессом. (Использовать основное термодинамическое соотношение)

15.Доказать что процесс Джоуля-Томсона (т.е. адиабатическое расширение от p до p+dp) является необратимым.

16.Доказать следующие свойства свободной энергии Гельмгольца: а) Система А находится в тепловом контакте с тепловым резервуаром R, имеющим температуру Т равную однородной температуре внутри системы. Изменение свободной энергии Гельмгольца F системы А равно изменению суммы внутренней энергии -системы А и теплового резервуара R при условии, что тепловой резервуар R отдает тепло только системе А и над резервуаром не производится никакой внешней работы. б) При изотермическом процессе работа, производимая над системой, равна увеличению ее свободной энергии.

17.Проверить выполнение теоремы Лиувилля для случая упруго сталкивающихся шаров с массами m1 и m2, движущихся по одной прямой.

18.Найти фазовой объем частицы массы m , свободно движущейся в объеме V.

19.Получить распределение Максвелла по абсолютным значениям импульсов и энергиям в нерелятивистском случае.

20.Идеальный газ находится в однородном поле тяготения при температуре Т. Масса

молекулы т. Ускорение свободного падения g. Концентрация газа у земной поверхности n0. Найти изменение концентрации с высотой.

21.Система N невзаимодействующих одномерных линейных гармонических осцилляторов с частотой ω, поддерживается при температуре Т. Найти характеристическую температуру, свободную энергию, энтропию, внутреннюю энергию, теплоемкость.

22.Система N одинаковых невзаимодействующих пространственных ротаторов,

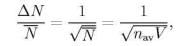
совершающих только вращательное движение. Момент инерции каждого ротатора I. Система поддерживается при температуре Т. Найти характеристическую температуру, свободную энергию, энтропию, внутреннюю энергию, теплоемкость.

23.Исследовать нормируемость распределения Больцмана для атмосферы планеты шарообразной формы радиуса R при постоянной температуре Т. Масса каждой молекулы атмосферы m. Ускорение свободного падения у поверхности планеты g.

24.Выразить энтропию квантового идеального газа через средние числа заполнения.

25. Идеальный газ, состоящий из N элементарных частиц с массой т и спином s, находится в объеме V при температуре Т. Спектр частиц можно считать непрерывным. Записать распределения частиц по импульсам и энергиям в нерелятивистском случае. Найти

химический потенциал как функцию температуры Т и концентрации п0 = N/V. Вычислить Ω- потенциал, внутреннюю энергию E , получить уравнение состояния.

26.Идеальный газ состоит из N частиц массой т и заполняет объем V при температуре Т. Получить условие снятия вырождения. Вычислить активность A0 больцмановского газа.

27.Показать, что для одноатомного идеального газа ,

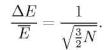
28.Показать, что для одноатомного идеального газа относительная флуктуация числа частиц

где nav - средняя концентрация частиц в подсистеме.

29. Доказать, что флуктуации температуры и числа частиц независимы друг от друга и подчинены закону Гаусса.

Необходимый минимум для положительной оценки.

Вразделе «термодинамика» необходимо знание трех начал термодинамики, понятие о том, какие величины являются или не являются функциями состояния и что это означает. Определение и свойства энтропии, определение и основные свойства таких характеристических функций как свободная энергия Гельмгольца, свободная энергия Гиббса. Необходимо знать, что такое химический потенциал. Нужно иметь представление о фазовых переходах первого и второго рода, их различии, о том каким образом меняются основные термодинамические величины при фазовых переходах первого и второго рода. Нужно иметь понятие о термодинамических силах, термодинамических потоках и их связи.

Вразделе «статистическая физика» нужно иметь понятие о различии термодинамического подхода к описанию больших систем от подхода статистической физики. Нужно знать распределения каноническое, микроканоническое и большое каноническое и знать в каких случаях применяется каждое из них. Нужно знать что такое статистическая сумма, зачем необходим ее расчет, связь статистической суммы с свободной энергией Гиббса и значение этого соотношения. Необходимо иметь представление о распределениях Максвелла, Больцмана, Ферми, Бозе – Эйнштейна и знать в каких случаях используется каждое из них. Необходимо иметь представление о вероятностном смысле энтропии, знать, что такое флуктуация и знать основную формулу для вероятности флуктуаций в изолированной системе.

Вразделе «физическая кинетика» надо знать о том, чему посвящен данный раздел

физики. Иметь представление об основных уравнениях кинетики Смолуховского, Фоккера – Планка, знать какой круг задач решается путем применения этих уравнений.