диплом киры

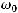
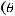
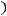
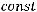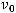
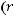
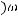
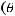
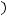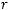
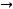
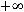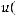
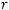
А так как , то имеет предел при . Тогда и функция 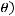имеет предел, равный при .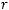

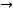
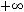Теорема доказана.

6.Заключение

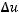
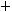
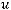
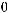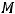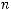
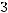
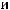
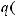
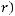
Врезультате работы были получены две теоремы. В теореме 2 указаны условия существования ограниченного решения Гельмгольца на сферически симметричном многообразие. Так же был приведён пример, в котором указано ограниченное решение уравнения на многообразии при 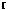, имеющее предел равный нулю при ,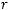

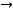
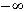
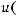
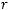
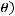
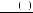
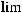
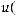
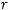
В теореме 3 указаны условия, при которых для каждого ограниченного решения Гельмгольца существует 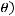, не зависящий от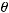

Литература

1.Г у с а р о в Л. А , Об ограниченности решений линейного уравнения второго порядка, ДАН СССР, т. LXVIII, № 2 (1949), 217—220.

2.Камке Э., Справочник по обыкновенным дифференциальным уравнениям, пер. с нем. 4-е изд., испр. — М.: Наука: Гл. ред. физ-мат. лит., 1971. — 576с.

3.Лосев А. Г., Мазепа Е. А. Об асимптотическом поведении решений некоторых уравнений эллиптического типа на некомпактных римановых многообразиях // Изв. вузов. Математика. 1999. Т. 445, № 6. С. 41–49.

4.Лосев А. Г., Мазепа Е. А. Ограниченные решения уравнения Шредингера на некомпактных римановых многообразиях специального вида // Докл. РАН. 1999. Т. 367, № 2. С. 166–167.

5.Соболь И. М., Исследование асимптотического поведения решений линейного дифференциального уравнения второго порядка при помощи полярных координат, МАТЕМАТИЧЕСКИЙ СБОРНИК .1951. Т. 28 (70), N. 3 .