
диплом киры
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
ФАКУЛЬТЕТ МАТЕМАТИКИ И ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
КАФЕДРА МАТЕМАТИЧЕСКОГО АНАЛИЗА И ТЕОРИИ ФУНКЦИЙ
«Допустить к защите»
_____________________
Заведующий кафедрой МАТФ д.ф.-м.н., доцент
Клячин Алексей Александрович
«__» ______________ 2012 г.
ВЫПУСКНАЯ КВАЛИФИКАЦИОННАЯ РАБОТА
по направлению подготовки бакалавров «Математика»
«ОБОБЩЕНОЕ РЕШЕНИЕ ГЕЛЬМГОЛЬЦА НА МОДЕЛЬНЫХ РИМАНОВЫХ МНОГООБРАЗИЯХ»
Выполнил: студент гр. Мб-081
Пучков Кирилл Андреевич
______________________________
Научный руководитель д.ф.-м.н., профессор:
Лосев Александр Георгиевич
______________________________
Волгоград, 2012
Содержание
1. |
Введение |
3 |
|
2. |
Вспомогательные утверждения |
|
|
|
2.1 |
Оператор Бельтрами-Лапласа на сферически симметричном многообразие |
3 |
|
2.2 |
Спектральное уравнение |
5 |
|
2.3 |
Ограниченные решения дифференциального уравнения второго порядка в |
|
|
нормальной форме |
6 |
|
3. |
Ограниченные решения Гельмгольца на сферически симметричном многообразие 6 |
||
4. |
Заключение |
11 |
|
5. |
Литература |
11 |
|

1.Введение
Вданной работе изучается поведение ограниченных решений уравнения Гельмгольца
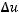
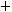
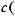
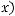
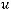

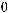 на некомпактных римановых многообразиях некоторого специального вида. В разделе 2.1 мы рассмотрим вид оператора Бельтрами-Лапласа на сферически симметричном многообразии, затем в пункте 2.2 получим так называемое спектральное уравнение и приведем его к нормальному виду. Используя теорему 1(Осцилляционная теорема) из пункта 2.3, сформулируем условия теоремы 2 и теоремы 3 .
на некомпактных римановых многообразиях некоторого специального вида. В разделе 2.1 мы рассмотрим вид оператора Бельтрами-Лапласа на сферически симметричном многообразии, затем в пункте 2.2 получим так называемое спектральное уравнение и приведем его к нормальному виду. Используя теорему 1(Осцилляционная теорема) из пункта 2.3, сформулируем условия теоремы 2 и теоремы 3 .
2.1 Оператор Бельтрами-Лапласа на сферически симметричном многообразие
Пусть 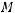
 сферически симметричное многообразие. Опишем данное многообразие подробнее.
сферически симметричное многообразие. Опишем данное многообразие подробнее.
Фиксируем начало координат 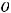
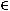
 и некоторую гладкую функцию
и некоторую гладкую функцию 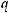 на интервале
на интервале 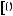
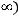 такую, что
такую, что 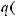



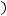

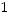 .
.
Определим наше многообразие 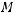 следующим образом:
следующим образом:
1) Множество точек 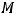 является открытым шаром в
является открытым шаром в 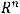 радиуса
радиуса 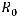

 , с центром
, с центром
в т.е. все
т.е. все 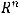
2)в полярных координатах 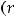
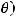 (где
(где 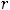
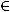
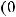
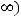 и
и 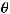
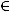
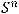

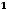 ) риманова метрика на
) риманова метрика на 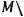
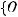
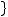 определяется как
определяется как
где 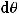
 стандартная риманова метрика на сфере
стандартная риманова метрика на сфере 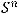

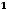 (в дальнейшем
(в дальнейшем 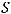 )
)
3) риманова метрика в 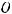 является гладким продолжением метрики
является гладким продолжением метрики 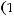
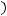

Рассмотрим на 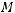 решения следующего уравнения
решения следующего уравнения
где 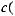
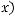 - гладкая, неотрицательная функция. Будем считаем, что на
- гладкая, неотрицательная функция. Будем считаем, что на 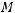 выполнены
выполнены
условия |
|
. |
|
|
|
|
|
||
Найдем вид оператора |
|
|
в координатах |
|
. Пусть |
|
риманов метрический |
||
|
|
||||||||
тензор на , |
|
|
, а |
|
элементы матрицы |
|
(т.е. контравариантные координаты |
||
|
|
|
|
||||||
|
|
|
|||||||
метрического тензора). |
|
|
|
|
|
|
|
||
В заданной метрике имеем
где 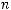

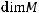
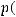
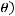
 определитель матрицы метрического тензора в метрике
определитель матрицы метрического тензора в метрике 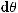
 на римановом многообразии
на римановом многообразии 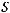 . Из вида метрики сразу следует, что
. Из вида метрики сразу следует, что

где 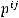
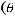
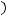
 элемент обратной матрицы метрического тензора на
элемент обратной матрицы метрического тензора на 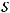 .
.
Подставляя полученные выражение в общую формулу оператора Лапласа-Бельтрами:
,
получаем
Вычисляя производные по переменной 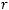 , получим
, получим
где

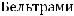
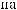
 .
.
Следовательно
общий вид оператора 
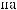
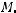
2.2 Спектральное уравнение и приведение его к нормальной форме.

Пусть 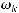
 ортонормированный базис в
ортонормированный базис в 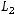
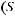
 из собственных функций оператора
из собственных функций оператора 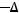
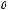 а
а 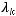
 соответствующие собственные числа. Будем считать, что собственные числа пронумерованы
соответствующие собственные числа. Будем считать, что собственные числа пронумерованы
в порядке возрастания, то есть выполнено 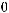

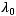

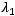
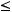
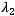
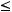
 Тогда для любого
Тогда для любого 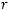 имеем:
имеем:
где
Подставим в |
и получим, что для любого индекса функция |
|
является решением уравнения |
т.е. для любого индекса 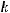 функция
функция 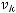
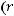
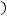 является решением обыкновенного дифференциального уравнения
является решением обыкновенного дифференциального уравнения
Данное уравнение играет важную роль при изучении свойств решений уравнения 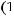
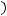 . В дальнейшем будем называть его спектральным.
. В дальнейшем будем называть его спектральным.
Приведем уравнение 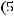
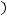 к так называемой нормальной форме, т.е. к следующему виду
к так называемой нормальной форме, т.е. к следующему виду
Произведём замену переменных
,
Подставим данные выражения в уравнение 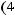
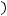 и получим, после сокращений, следующее:
и получим, после сокращений, следующее:

Используя обозначение 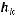
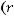
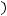


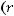
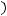

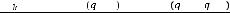
 , приведем наше дифференциальное уравнение к нормальному виду
, приведем наше дифференциальное уравнение к нормальному виду
2.3 Ограниченные решения дифференциального уравнения второго порядка в нормальной форме.
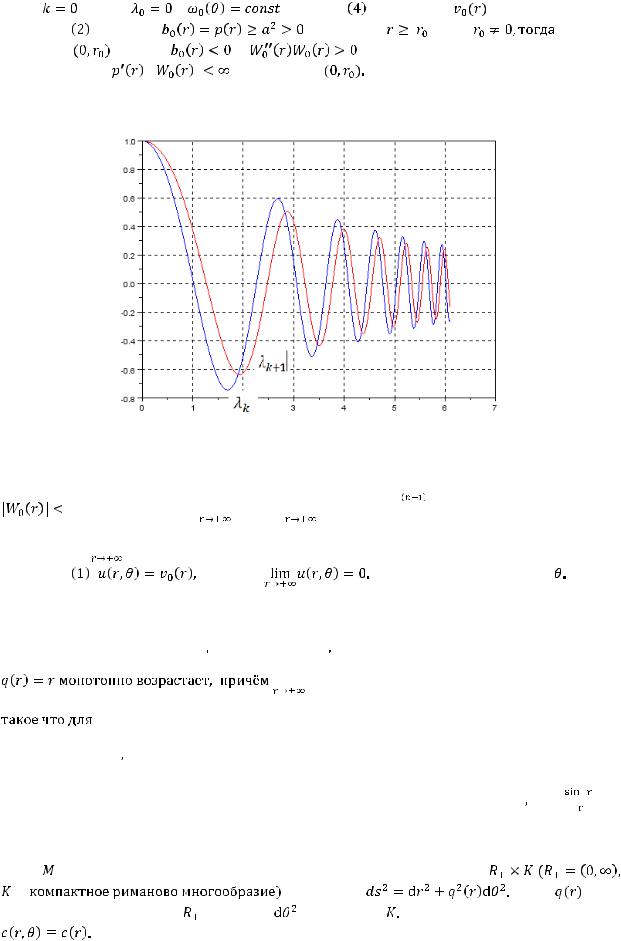
Для исследования свойств решений дифференциального уравнения второго порядка в нормальной форме существует ряд теорем. Следующая теорема позволяет нам утверждать, что при выполнении ряда условий все решения уравнения 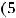
стремятся к нулю на бесконечности.
Теорема 1(Осцилляционная теорема) Если для любого |
выполнены следующие |
||
условия: |
|
непрерывна и ограничена, то все решения уравнения |
|
|
|||
ограничены, имеют бесконечно много нулей, причем амплитуды колебаний монотонно
убывают. Если кроме того |
, то все решения уравнения |
стремятся к |
нулю при |
|
|
3. Ограниченные решения Гельмгольца на сферически симметричном многообразие
Введем следующее обозначение |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
Теорема 2 Пусть |
|
|
|
|
|
|
|
|
|
|
|
. Пусть |
существует |
|||
|
|
|
|
|
|
|
|
|
|
|
выполнены |
следующие условия: |
||||
|
|
|
непрерывна и ограничена при |
|
|
тогда |
на |
существует |
||||||||
|
|
|
|
|
||||||||||||
ограниченное решение |
уравнения |
|
|
имеющее предел равный |
||||||||||||
нулю при |
|
Доказательство |
|
Из условия теоремы следует, что для некоторого |
выполнено: |
для всех |
|
непрерывна и ограниченной вариации, кроме того |
. |
|
Пусть |
, то есть |
и |
. Тогда из |
следует, что |
является решением |
|||
уравнения . Ясно, что |
|
для любого |
. Пусть |
на |
||||
интервале |
|
функция |
|
и |
, следовательно в силу непрерывности и |
|||
ограниченности |
, |
|
|
на интервале |
|
|
|
|
|
|
|
|
|
||||
Применяя теорему 1 для дифференциального уравнения в нормальной форме, получим, что
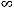 , и следовательно
, и следовательно 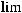
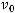
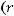
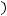

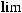
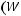
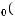

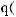
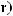

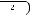

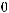 .
.
Учитывая, что 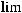
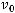
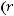
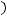

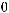 можно утверждать следующее: существует ограниченное решение
можно утверждать следующее: существует ограниченное решение
уравнения , |
такое что |
При этом оно не зависит от |
Теорема доказана.
Пример Пусть 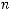

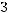
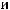
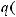
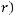

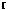
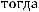
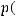
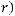

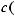

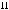 оложим
оложим 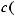
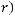

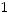
 Заметим, что
Заметим, что
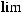
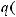
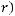

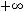 .
. 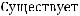

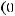
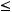
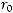
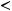
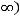
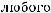
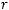
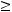
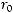
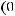
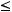
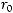
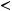
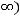 выполнены следующие условия:
выполнены следующие условия:
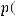
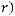

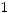
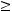
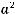
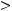

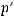
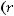
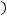

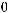
 непрерывна и ограниченной вариации. То есть выполняются условия теоремы 2, и следовательно существует нетривиальное ограниченное решение уравнения
непрерывна и ограниченной вариации. То есть выполняются условия теоремы 2, и следовательно существует нетривиальное ограниченное решение уравнения 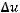
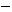
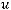

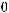 имеющее предел равный нулю при
имеющее предел равный нулю при 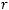
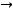
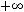
 Например
Например 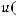
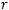
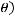

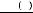

Пусть |
|
риманово многообразие изометричное прямому произведению |
|
|||||||
|
|
|||||||||
|
|
|
|
|
|
с метрикой |
Здесь |
– |
||
|
|
|
|
|
|
|||||
положительная, гладкая на |
функция, а |
|
|
метрика на |
В дальнейшем будем считать, что |
|||||
|
|
|||||||||

Теорема 3 Пусть 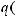
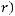
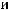
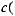
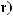 монотонно убывают, причём
монотонно убывают, причём
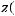
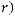

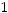

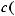
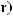
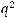
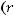
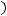
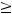
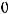 для любого
для любого 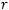
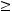
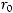
 На многообразии
На многообразии 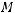 выполнено условие
выполнено условие
где |
|
а |
из уравнения (2). Тогда для любого ограниченного решения |
|
уравнения (2) существует |
|
|
, не зависящий от |
|
Доказательство |
|
|
|
|
В координатах |
на |
оператор |
имеет вид |
|
где 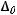
 внутренний лапласиан на
внутренний лапласиан на 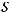 . Формула
. Формула 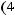
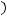 проверяется непосредственно по определению оператора Лапласа-Бельтрами.
проверяется непосредственно по определению оператора Лапласа-Бельтрами.
Пусть 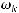
 ортонормированный базис в
ортонормированный базис в 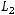
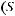
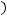 из собственных функций оператора
из собственных функций оператора 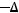
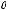 а
а 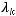
 соответствующие собственные числа. Будем считать, что собственные числа пронумерованы
соответствующие собственные числа. Будем считать, что собственные числа пронумерованы
в порядке возрастания, то есть выполнено 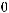

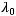
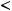

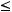
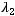
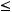
 Тогда для любого
Тогда для любого 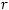 имеем:
имеем:
где
Из 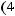
 следует, что для любого индекса
следует, что для любого индекса 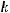 функция
функция 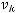
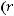
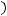 является решением обыкновенного дифференциального уравнения
является решением обыкновенного дифференциального уравнения
Докажем сначала, что в условиях теоремы |
|
|
|||||||
для любого номера |
|
|
|
|
|
|
|
|
|
Из ограниченности |
и |
следует ограниченность |
|
для любого номера |
|||||
Дважды интегрируя уравнение |
|
, получаем равенство |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

где числа |
|
любые. |
|
|
|
|
|
|
Легко показать, что если при каком-то |
выполнено |
|
|
|
причем |
и |
||
не равны 0 одновременно, то из |
следует, что |
|
|
при |
. Тогда из |
|
||
|
|
|
||||||
ограниченности |
следует, что для любого |
либо |
|
, |
|
|||
либо |
. В первом случае по теореме единственности |
|
. Покажем, что во |
|||||
втором случае имеет место |
Домножив при необходимости на -1, можно считать, что при всех |
|||||||
|
|
. . Таким образом |
монотонно возрастает и |
|
||||
Пусть
Тогда при некотором 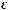
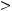
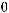 и всех
и всех 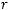
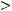
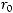 выполнено
выполнено
Покажем, что условие 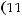
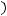 противоречит расходимости интеграла
противоречит расходимости интеграла 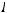 . Заметим, что
. Заметим, что
Перепишем равенство 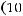
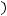 в виде
в виде
где
-монотонно убывающая функция в силу отрицательности 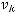
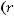
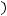 . Если
. Если
то из 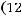
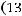
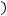 следует, что
следует, что 
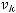

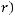

 при
при 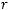
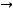
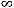 .. Поэтому
.. Поэтому
и, стало быть, выполнено равенство
Тогда из 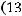
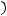 следует, что
следует, что
Так как выполнено 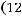
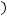
Тем самым, для любого 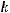
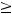
 выполнено
выполнено
Тогда из предположения 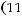
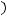 получаем,
получаем, 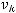
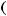
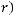
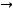

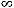 при
при 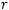
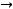
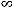 . Следовательно, справедливо
. Следовательно, справедливо 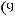
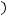
 Докажем далее, что для любой константы
Докажем далее, что для любой константы 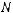 выполнено
выполнено

Используя формулу Грина и определение 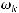
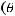
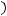 , для
, для 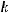
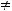
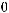 получаем
получаем
Применяя формулу Грина 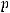 раз (где
раз (где 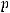
 произвольное натуральное число)получим
произвольное натуральное число)получим
Применяя к правой части неравенство Коши-Буняковского, имеем
где 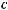
 константа зависящая от
константа зависящая от 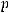 .Так как
.Так как 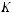
 компакт, то из асимптотики Вейля следует, что существует положительная константа
компакт, то из асимптотики Вейля следует, что существует положительная константа 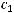 такая, что при достаточно больших
такая, что при достаточно больших 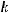 выполнено
выполнено
где 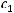
 константа зависящая от
константа зависящая от 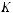 .
.
Поэтому, учитывая неравенство 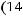
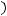 , получаем
, получаем
где 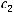
 константа зависящая от
константа зависящая от 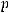 .
.
Заметим, что для достаточно больших 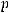
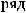
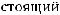
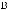
Из теоремы* следует справедливость неравенства 
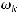
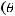
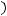

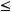
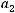
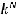
 , где
, где 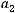 и
и 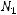
 константы, зависящие от
константы, зависящие от 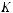 . Тогда справедливы следующие неравенства
. Тогда справедливы следующие неравенства
и при достаточно большом 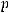 ряд сходится. Следовательно ряд
ряд сходится. Следовательно ряд 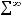
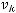
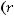
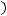
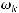
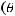
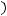
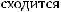 абсолютно и равномерно. Учитывая, что
абсолютно и равномерно. Учитывая, что 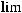
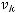

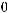 можно показать следующее равенство
можно показать следующее равенство
