Оптика пронизывает всю жизнь и все производства. Куда бы человек ни двинулся в науке и технике, всюду он окружен оптикой и оптическими инструментами. Там, где мы хотим узнать что-нибудь с большой точностью, увидеть каналы на Марсе, наблюсти хвостик споры толщиной в 0,1 микрона, мы всегда обращаемся к лучу света, к возможно короткой волне. Народы славятся своей оптической индустрией.

Д.С. Рождественский

ЛАБОРАТОРНАЯ РАБОТА № 4. БИОЛОГИЧЕСКИЙ МИКРОСКОП

1 ЦЕЛЬ И ЗАДАЧИ ЛАБОРАТОРНОЙ РАБОТЫ Лабораторная работа выполняется с целью изучения принципиальной

оптической схемы биологического микроскопа и ее основных оптических характеристик; получения навыков проведения габаритного расчета, компьютерного проектирования и оценки качества изображения оптических систем указанного типа. В процессе выполнения лабораторной работы студенту необходимо решить следующие задачи:

1)провести габаритный расчет двухкомпонентной схемы микроскопа, обеспечивающей заданное разрешение;

2)осуществить выбор компонентов системы из архивов оптических систем и компоновку схемы;

3)провести проверочный расчет оптической системы микроскопа по программам автоматизированного расчета оптики и проанализировать параксиальные и аберрационные характеристики полученной системы;

4)получить навыки оформления оптических схем биологических микроскопов и выпуска рабочих чертежей оптических деталей.

2 КРАТКОЕ ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ Оптическая система биологического микроскопа содержит осветительную

систему и наблюдательную, которую в дальнейшем и будем называть микроскопом. В состав последней входят два основных оптических элемента: объектив и окуляр – и дополнительно могут включаться призменные системы, предназначенные для изменения направления оптической оси, а также для бинокулярной насадки. На рисунке 4.1 представлена оптическая схема двухкомпонентного микроскопа в тонких компонентах с ходом осевого и наклонного пучков лучей. Ход луча, идущего в пространстве предметов параллельно оптической оси, обозначенного стрелкой, показан для определения положения заднего фокуса и задней главной точки микроскопа.

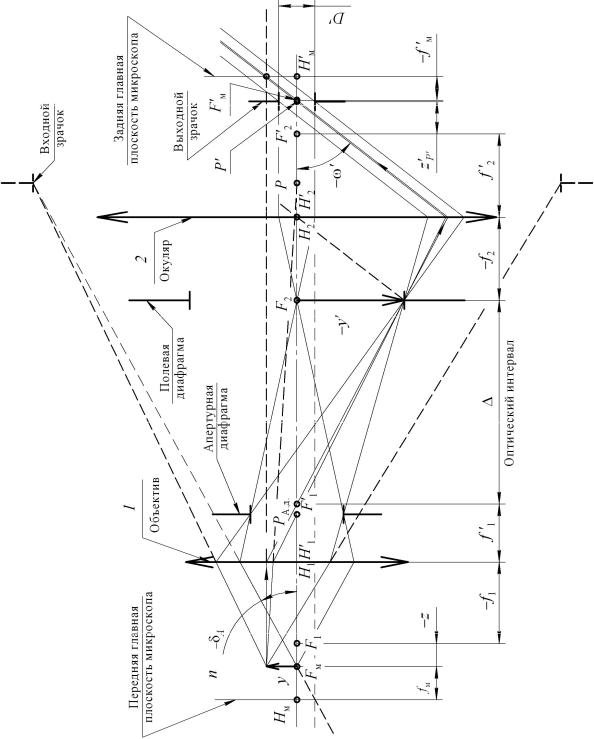
Рисунок 4.1 – Оптическая схема двухкомпонентного микроскопа в тонких компонентах

Объектив О1 строит увеличенное действительное изображение объекта y в

передней фокальной плоскости окуляра или вблизи неё. Это изображение (y') рассматривается глазом через окуляр O2 , причем в зависимости от положения

промежуточного изображения относительно фокуса F2 изображение

проецируется либо на бесконечность, либо на расстоянии наилучшего зрения наблюдателя.

Величина называется оптическим интервалом, или оптической длиной тубуса микроскопа. При постоянной механической длине тубуса величина несколько отличается для объективов разных увеличений. В случае использования иммерсии в пространстве предметов микроскопа находится среда с показателем преломления n, отличным от 1 (водная, масляная, глицериновая и другие иммерсионные жидкости).

Габаритный расчет проводится для положения изображения в бесконечности. Фокусные расстояния микроскопа определяются по формулам эквивалентной системы из двух компонентов:

f'м = − f'1 f'2 / и f м = f1 f 2 / . (4.1)

Положение фокусов микроскопа может быть определено по формулам

zF = f1 f'2 / , z'F' = − f2 f'1 / . (4.2)

Оптическая система микроскопа является примером положительной оптической системы с отрицательным задним фокусным расстоянием.

Апертурной диафрагмой в биологическом микроскопе может являться либо оправа объектива (простые по конструкции объективы малых увеличений и апертур), либо оправа последней линзы объектива, либо специальная диафрагма. В последних двух случаях апертурная диафрагма обычно располагается вблизи задней фокальной плоскости объектива. Ее проекция за окуляром определяет диаметр D' выходного зрачка и его положение. При положении апертурной диафрагмы между задней главной и задней фокальной плоскостями объектива входной зрачок является мнимым.

Числовая апертура микроскопа определяется числовой апертурой объектива

А = n sinσ A .

Линейное увеличение объектива

где ω – угол, под которым наблюдается объект невооруженным глазом с расстояния наилучшего зрения;

ω' – угол, под которым наблюдается изображение объекта через окуляр микроскопа.

Выходной зрачок микроскопа расположен близко к заднему фокусу микроскопа и наблюдается в виде светлого кружка, с которым совмещается зрачок глаза при наблюдении в микроскоп. Так как выходной зрачок микроскопа

обычно меньше зрачка глаза наблюдателя, то последний не оказывает влияния на ограничение пучков в микроскопе. Действительно, для полезных увеличений микроскопа (см. далее формулу 4.12) диаметр выходного зрачка микроскопа, вычисленный в соответствии с формулой 4.5, лежит в пределах от 0,5 до 1 мм.

В плоскости действительного промежуточного изображения микроскопа устанавливается полевая диафрагма, диаметр которой

Предел разрешения микроскопа физически ограничен явлением дифракции на элементах микрообъекта, рассматриваемого в микроскоп. Предел разрешения задается либо линейным размером δ наименьшего разрешаемого элемента в плоскости предмета, либо числом N разрешаемых линий на 1 мм в той же плоскости. Если оптическая система микроскопа хорошо корригирована, и остаточные аберрации не оказывают влияния на качество изображения, то

где Ao , A – числовая апертура осветителя и микроскопа соответственно. Если числовые апертуры осветителя и микроскопа равны, то

Если увеличение микроскопа таково, что видимый размер изображения минимально разрешаемого элемента δ за окуляром микроскопа соответствует

разрешающей способности глаза наблюдателя (величина которой принимается 2 ¸ 4 угловых минуты), то такое увеличение микроскопа называют полезным Γп . Его величина для видимого диапазона излучения соответствует неравенству:

Формула (4.12) не относится к микропроекции и микрофотографии, так как при наблюдении изображений на экране зрачок глаза не ограничивается выходным зрачком микроскопа, и разрешающая способность глаза может быть

аккомодированный на определенную плоскость изображения, не замечает расфокусировки:

Если глаз имеет объем аккомодации А (в дптр), то глубина изображаемого пространства увеличивается на величину Так:

f'2 ×A

Tак = м . (4.15) 1000

В частности, для А = 4 дптр получается Tак = 250 .

Gм2

Общая глубина резко изображаемого пространства определяется суммой составляющих, определяемых по формулам (4.13) и (4.15). При наличии сетки в поле зрения наблюдателя аккомодационная составляющая Так будет отсутствовать.

Объективы микроскопов имеют увеличения от 3 до 90х и числовую апертуру от 0,01 до 1,4. Различают ахроматы, апохроматы, планахроматы, планапохроматы, монохроматы, зеркальные и зеркально-линзовые, телецентрические объективы, объективы с применением флюорита и т. д., а также сухие и иммерсионные. Конструкция объективов зависит от типа, увеличения и числовой апертуры. Объективы средних и больших апертур рассчитываются с учетом покровного стекла. Оно изготавливается толщиной

0,17 ± 0,01 мм.

В микроскопах применяют окуляры следующих типов: Гюйгенса, Кельнера, компенсационные, симметричные, ортоскопические, панкратические, гомалы, специальные.

Допустимые значения остаточных аберраций в микроскопе. В

микроскопах угловые аберрации за окуляром могут быть больше, чем в телескопических системах, так как объекты часто являются малоконтрастными, имеют недостаточную освещенность, диаметр выходного зрачка микроскопа может быть меньше диаметра зрачка глаза и, как результат, разрешающая способность глаза ниже, чем при оптимальных условиях наблюдения. В центре поля в оптической системе микроскопа сферическая и хроматическая аберрации могут достигать 10' и более.

Продольные аберрации объективов больших увеличений (60 – 90 х) могут достигать нескольких миллиметров, но в силу малости задней апертуры объектива поперечные аберрации оказываются малыми. Для оценки качества аберрационной коррекции объективов часто используются волновые аберрации. Их величина не должна превышать 0,1 λ для объективов больших апертур и 0,25 λ – для объективов средних и малых апертур. Отступление от условия синусов не более 0,1 – 0,2%. Хроматическая разность сферических аберраций должна быть в несколько раз меньше, чем сферическая аберрация для основной длины волны.

Для более глубокого изучения материала следует обратиться к учебникам и монографиям, например, [1, с. 376 – 385 ], [4], [9].

ПОРЯДОК ВЫПОЛНЕНИЯ 3 ЛАБОРАТОРНОЙ РАБОТЫ

Лабораторная работа выполняется студентом в соответствии с индивидуальным заданием. Исходными данными для разработки оптической схемы микроскопа является величина разрешающей способности. Она задается наименьшей величиной δ предмета, который разрешается глазом при наблюдении в микроскоп. Величина δ приведена в таблице 4.1 для различных вариантов лабораторной работы.

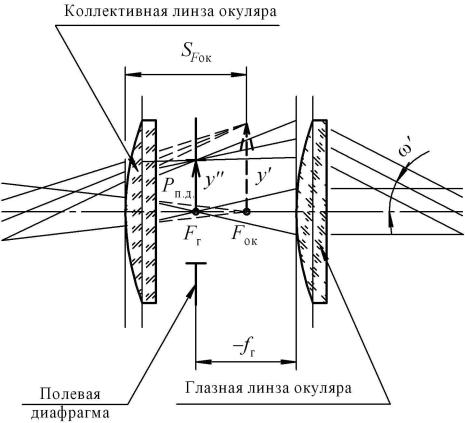
Рисунок 4.2. Принципиальная оптическая схема окуляра Гюйгенса Таблица 4.2. Параметры окуляров Гюйгенса

Полевая диафрагма расположена в плоскости действительного изображения y'',с которой совмещается передняя фокальная плоскость глазной линзы окуляра. Диаметр полевой диафрагмы:

Обычно βк < 1 . В случае использования окуляра Гюйгенса формула (4.6) примет вид:

1)Для выбранного окуляра рассчитать диаметр полевой диафрагмы по формуле (4.16), ее положение, а также положение фокальных плоскостей окуляра. Расчеты провести либо по формулам идеальной оптической системы,

либо по компьютерной программе. Принять угловое поле окуляра в пространстве изображений равным 25о.

2)Рассчитать величину линейного поля в пространстве предметов микроскопа (формулы (4.17) и (4.3)).

3)Рассчитать по формулам идеальной оптической системы положение и размер выходного зрачка микроскопа (формулы (4.8), (4.9)).

4)Вычислить расстояния между последней поверхностью объектива и первой поверхностью окуляра. Дать эскиз оптической схемы микроскопа с указанием конструктивных параметров, необходимых для проверочного расчета схемы на компьютере.

5)Провести проверочный расчет оптической схемы. Убедиться, что изображение после окуляра находится в бесконечности, микроскоп имеет требуемые величины видимого увеличения, диаметра выходного зрачка, углового поля в пространстве изображений, а также достаточное удаление выходного зрачка для совмещения с ним зрачка глаза наблюдателя. Провести анализ остаточных аберраций системы, сравнив их с допустимыми.

6)Рассчитать коэффициент пропускания микроскопа, глубину резко изображаемого пространства, величину диоптрийной подвижки окуляра на одну диоптрию и прочие характеристики, необходимые для выполнения схемы и чертежей.

7)Выполнить чертеж принципиальной оптической схемы микроскопа и рабочие чертежи оптических деталей (2-3 чертежа по указанию преподавателя) в соответствии с действующими стандартами. На схеме указать следующие характеристики: видимое увеличение; линейное поле оптической системы в пространстве предметов; числовую апертуру в пространстве предметов; предел разрешения; диаметр выходного зрачка; удаление выходного зрачка от последней поверхности; коэффициент пропускания, перемещение окуляра на 1 дптр.

8)Оформить отчет по лабораторной работе.

4 СОДЕРЖАНИЕ ОТЧЕТА ПО ЛАБОРАТОРНОЙ РАБОТЕ

1)Габаритный расчет микроскопа в соответствии с п. 3, оптическая схема

втонких компонентах с ходом осевого и наклонного пучков лучей.

2)Эскиз оптической схемы, её конструктивные параметры, результаты расчета параксиальных характеристик, световых диаметров и аберраций.

3)Графики волновой аберрации объектива и графики аберраций всей системы. На каждом графике указать значения аберраций.

4)Выводы по лабораторной работе: а) соответствие параметров разработанной оптической системы заданию на лабораторную работу; б) оценка качества изображения по величинам остаточных аберраций в разработанной системе;

5)Чертеж принципиальной оптической схемы и рабочие чертежи деталей. 5 ВОПРОСЫ ДЛЯ ЗАЩИТЫ

1)Принципиальная оптическая схема микроскопа, основные параметры и соотношения.

2)От чего зависит разрешающая способность микроскопа?

3)Какое увеличение микроскопа называется полезным?

4)Входной и выходной зрачки, апертурная диафрагма, числовая апертура микроскопа.

5)От чего зависит глубина резко изображаемого пространства в микроскопе?

6)От каких параметров зависит величина линейного поля микроскопа?

7)Механическая и оптическая длины тубусов.

8)Основные типы объективов микроскопов.

9)Основные типы окуляров микроскопов.

10)Оптическая схема окуляра Гюйгенса.

11)Методика габаритного расчета оптической схемы биологического микроскопа.

12)Понятие волновой аберрации.

13)Оценка качества изображения оптической системы микроскопов по результатам аберрационного расчета.

14)Схема микропроекции с отрицательным окуляром.

15)Решить задачу по данной теме по указанию преподавателя (см. приложение А. Задачи к лабораторной работе № 4).