TI_v_EMM_2014

вычисления производятся каждым игроком независимо в предположении, что остальные игроки делают то же самое. Только в этом ограниченном смысле сложное поведение можно назвать изолированным.

Разрешимость по доминированию игры Г означает, что после конечного числа раундов исключений все стратегии каждого игрока станут для него эквивалентными (но не обязательно для всех – см. пример 2).

Тема 2. Лекция 6. Равновесия Нэша в смешанных стратегиях.

4. Смешанные стратегии

При построении нормальной формы игры по ее развернутой форме, множества стратегий развернутой игры превращаются во множества действий игры в нормальной форме. Зачастую действие игрока в игре в нормальной форме также называют стратегией. Это не совсем верно. Обычно термин «стратегия» имеет более широкий смысл и используется для обозначения плана, который каждый игрок составляет до начала игры. Этот план описывает все действия, которые игрок будет предпринимать во всех возможных игровых состояниях. Стратегия игроков даже в игре в нормальной форме может быть более

сложной, чем просто выбор одного из элементов множества действий X i (стратегия, состоящая в выборе действия из множества X i , называется чистой стратегией).

Вспомним, что в играх в развернутой форме для тех ходов, которые делала природа, указывалась вероятность того или иного ее «хода». Аналогично и игроки могут не выбирать в каждой ситуации некоторое единственное действие, а выбирать одно из действий с некоторой вероятностью. Тогда выбор игрока будет описываться вероятностным распределением на множестве возможных в данной игровой ситуации действий, которое называется смешанной стратегией. Оказывается, что такое поведение в некоторых ситуациях может привести игрока к более выгодному распределению полезностей.

Определение 4: Смешанной стратегией X i i-гo игрока (i N ) для игры в нормальной форме

смешанных стратегиях для i-гo игрока, i N .

Ожидаемый выигрыш игроков при использовании ими смешанных стратегий будет вычисляться как

математическое ожидание их функции выигрыша. Для дискретных игр

~

Ki ( ) Ki (xi , x i ) i (xi ) i (x i ),i N.

xi X i x i X i

Смешанная стратегия для непрерывных игр представляет собой вероятностную меру на множестве чистых стратегий игрока. Ожидаемая полезность игроков при использовании ими смешанных стратегий будет интегралом функции полезности по декартову произведению этих вероятностных мер.

Дискретную игру, в которой игроки используют смешанные стратегии, можно привести к непрерывной игре, в которой игроки используют только чистые стратегии. Это достигается путем замены множества чистых стратегий игрока на множество его смешанных стратегий, а функции выигрыша – ее математическим ожиданием.

32

Тогда можно исследовать свойства новой игры в предположении, что игроки используют только чистые стратегии. Это, однако, не всегда бывает удобным, так как такой переход приводит к замене более простой, дискретной игры, более сложной – непрерывной

Приведем несколько свойств смешанных стратегий в дискретных играх.

Лемма 1. Ожидаемая полезность дискретной игры – непрерывная функция смешанных стратегий. Теорема 2. Для произвольной обстановки в смешанных стратегиях найдется чистая стратегия,

являющаяся «наилучшим ответом» на данную обстановку, то есть

стратегию, не являющуюся лучшим ответом на обстановку i , не будет и сама лучшим ответом на обстановку i

Доказательство. Множество смешанных стратегий - это компакт, в котором содержатся и чистые стратегии. Для игрока i зафиксируем обстановку в смешанных стратегиях i . Тогда ожидаемый выигрыш

максимальный ожидаемый выигрыш, возможный при использовании смешанных стратегий. Значит, неравенство можно заменить равенством, а это, в свою очередь, значит, что максимальный ожидаемый выигрыш достигается на не которой чистой стратегии. Кроме того, если любой не максимальный элемент

(3) входит в сумму (2) с ненулевым весом, то ожидаемая полезность будет строго меньше максимально возможной и смешанная стратегия не будет наилучшим ответом на обстановку i .

Смешанные стратегии – довольно хрупкая конструкция. Их использование в ряде практических задач неоднократно подвергалось критике. Один из аргументов против использования смешанных стратегий таков: «Применение смешанных стратегий подходит только для игр с большим числом повторений. Рассмотрим игру, которая должна быть сыграна лишь один раз. При использовании смешанных стратегий игрок должен выбирать свое решение на основании реализации случайного процесса, задаваемого распределением вероятности его смешанной стратегии. Однако эта реализация может дать стратегию, настолько «экзотическую», что ее применение в единичной игре будет малоэффективно, несмотря на теоретические обоснования эффективности такой смешанной стратегии в смысле среднего выигрыша на протяжении многих игр».

Поэтому, когда возможно, особенно при моделировании реальных систем, следует использовать только чистые стратегии.

Стремление к устойчивости решений является широко распространенным способом формулирования принципов рационального поведения в теории игр. Самый популярный принцип рационального поведения в теории некооперативных игр рекомендует в качестве рациональных исходов использовать ситуации равновесия Нэша. Они характеризуются тем, что отклонение от данной ситуации равновесия одним из игроков не может увеличить его выигрыша, и, таким образом, рациональной стратегией каждого игрока должна быть реализация равновесия. Можно сказать, что ситуация называется равновесной по Нэшу, если она устойчива относительно индивидуального отклонения игроков.

Определение 12: Ситуация x*=(x1*,x2*,…,xn*) называется ситуацией равновесия по Нэшу (в чистых стратегиях), если для всех х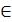i, Хi„ i N справедливо неравенство Ki (xi*,x-i*) Ki (xi*,x-i*)

33

Определение 13: Совокупность всех равновесных по Нэшу ситуаций игры называется множеством равновесий Нэша.

Если ситуация - равновесие Нэша, то никому из игроков не выгодно в одиночку отклоняться от нее. Однако возможно, что, объединившись, игроки могут улучшить свое положение выходом из равновесия Нэша.

смешанной стратегии χ, любого игрока справедливо неравенство (χ1*,χ-i*)(χ1*,χ-i*),

где(.) – результат усреднения функций выигрыша игроков по используемым ими смешанным стратегиям.

Множество равновесий Нэша в чистых стратегиях может оказаться пустым для некоторых игр, и возможное отсутствие равновесных ситуаций является большим недостатком равновесия Нэша в чистых стратегиях.

Теорема 3 (Теорема Дж. Нэша). Для произвольной дискретной игры существует, по меньшей мере, одно равновесие Нэша в смешанных стратегиях.

Доказательство. Множество смешанных стратегий каждого игрока - непустой выпуклый компакт (ограниченное и замкнутое множество) в конечномерном пространстве. Обозначим множество наилучших ответов игрока на произвольную обстановку

множество, так как оно представляет собой ограниченное линейными неравенствами подмножество выпуклого множества смешанных стратегий. Определим многозначное соответствие

которое ставит в соответствие каждой ситуации множество - декартово произведение множеств стратегий – наилучших ответов каждого игрока на обстановку, заданную остальными компонентами ситуации. Для произвольной ситуации в смешанных стратегиях χ, R(χ) является непустым, выпуклым компактом (так как является декартовым произведением непустых, выпуклых компактов)

Для дальнейшего доказательства воспользуемся теоремой Какутани. Введем сначала определение: Определение 15: Многозначное отображение F компакта S в себя называется полунепрерывным

ставит в соответствие каждой точке S непустое выпуклое подмножество S, то существует такой χ* S, χ*

F(χ*).

Покажем, что отображение R полунепрерывно сверху. Для этого рассмотрим произвольные сходящиеся последовательности χk и из определения полунепрерывности сверху.

(σi, χ-i), то есть ρ R(χ).

По теореме Какутани, существует неподвижная точка – ситуация χ*, такая, что χ* R(χ*).

Значит, для всех игроков (χ*, χ*-i) ≥ (χi, χ-i*), где χi –произвольная смешанная стратегия. То есть χ*– это равновесие Нэша.

Аналогичные результаты можно получить и для бесконечных игр, например, справедлива Теорема 5. Если множества стратегий игроков компактны, а функции выигрыша непрерывны по

совокупности переменных (чистых стратегий игроков), то в игре существует, по крайней мере, одно равновесие Нэша в смешанных стратегиях.

На основании полученных результатов можно сформулировать одно из возможных достаточных условий существования равновесия в чистых стратегиях:

Теорема 6. Если в непрерывной игре множества стратегий Xi - выпуклые подмножества линейных метрических пространств, для каждого игрока i функция выигрыша Кi непрерывна по всем переменным и строго вогнута по переменной хi , то в этой игре существует равновесие Нэша в чистых стратегиях.

34

Доказательство. Согласно теореме 2 наилучший ответ всегда достигается на чистых стратегиях. Необходимо показать, что следствием вогнутости целевых функций является единственность наилучшего ответа. Это будет означать, что наилучшим ответом может быть только чистая стратегия. Тогда и равновесие Нэша будет состоять только из чистых стратегий.

Введем обозначение Х*(χ-i ) = Arg max Кi (хi ,χ-i ) - множество чистых стратегий, которые являются

наилучшими ответами на обстановку χ-i. Пусть имеются два наилучших ответа x*i X*i и xi** Xi*. Так как

оба они являются лучшими ответами на обстановку χ-i значит Кi (xi*, χ-i) = Кi (хi**, χ-i), то есть

M: =∫Ki (xi*,x-i)χ-i(x-i)dx-i = ∫ Ki (xi**, x-i)χ-i(x-i)dx-i.

Рассмотрим стратегию = αxi* + (1-α)xi**, где α (0,1).В силу выпуклости Хi,, Xt. Ожидаемая полезность от применения этой стратегии:

Ki (, χ-i) = ∫ Ki (, x-i) χ-i(x-i)dx-i =∫ Ki (xi*+(1-α) xi**,x-i) χ-i(x-i)dx-i.

В силу строгой вогнутости целевой функции Кi, имеем Кi ( ,χ-i)>α∫Ki (xi*,x-i)χ-i(x-i)dx-i +(1-α) ∫Ki

(xi**,x-i)χ-i(x-i)dx-i.

Следовательно, Ki (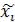, χ-i) > αM + (1-α)M = M, что невозможно, так как М- это максимальный ожидаемый выигрыш. Таким образом, наилучший ответ всегда один, а, значит, и равновесие Нэша будет равновесием в чистых стратегиях.

Наличие нескольких равновесий Нэша порождает некоторые проблемы, ведь в идеальном случае концепция решения должна точно предсказывать результат игры, что возможно лишь при однозначном определении рациональных стратегии всех игроков.

Одним из выходов является констатация того, что ситуации равновесия Нэша не являются точным и единственным решением, а являются лишь набором рациональных стратегии поведения, выбор из которых нельзя произвести на основе имеющихся данных.

Равновесие Нэша подвергается справедливой критике, ведь чтобы результатом игры было равновесие Нэша, все игроки должны выбрать именно равновесную ситуацию, при этом предварительно конкретизировав одну из равновесных ситуаций в случае, когда равновесий много.

Тема 3. Антагонистические игры (игры с нулевой суммой). Платежная матрица. Чистые стратегии. Цена игры. Седловая точка платежной матрицы. Теорема о минимаксе.

Определение. Игра двух лиц, в которой в каждом исходе выигрыш одного из игроков равен проигрышу другого, называется антагонистической (матричной) игрой или игрой с нулевой суммой. При этом

-множество игроков состоит из двух элементов {A,B};

-FA (или FB) – функции выигрыша;

-матрица А выигрышей игрока А (она же – матрица проигрышей игрока В) называется платежной

матрицей: aij=FA(y(i)A,y(j)B),

-SA,SB – множества стратегий игроков (чистых стратегий) представляют собой множества номеров

Пример 1. Фирма А производит сезонный товар, который поставляется на рынок в момент времени i. Фирма В конкурирует с фирмой А (цель фирмы В – разорить фирму А) и поставляет на рынок товар в момент времени j=1,…,n – в начале каждого периода времени. Размеры фирм равны, цена товара фиксирована, а качество определяется моментом времени его поступления (чем позже товар поступил, тем он качественней). На рынке продается только более качественный товар. Доход от продаж в единицу времени равен С, число периодов времени n=4.

Строим платежную матрицу игры:

В

35

Табл. Платежная матрица (доход фирмы А равен убытку фирмы В).

j 0 , и значит .

36

Пример 3. Две конкурирующие финансовые компании ведут переговоры с организаторами трех проектов. Задача фирмы В – профинансировать любой проект. Задача фирмы А – сорвать переговоры. Стратегии фирмы А:

1)предложить более выгодные условия;

2)опорочить фирму В.

Стратегия фирмы В: выбрать проект для финансирования.

Платежная матрица содержит значения вероятности срыва переговоров.

Тема 3. Лекция 8. Антагонистические игры. Смешанные стратегии. Теорема фон Неймана.

Пусть задана антагонистическая игра с платежной матрицей A (m, n) = (|aij|). Кроме того. Предположим. Что игра не имеет цены в чистых стратегиях. Будем предполдагать, что игра разыгрывается многократно. Тогда игроки могут в разных розыгрышах использовать различные стратегии.

Определение. Смешанной стратегией игрока А называется дискретная случайная величина, принимающая значения 1,2,3,…m с определенной вероятностью; . смешанной стратегией игрока В называется дискретная случайная величина, принимающая значения 1,2,3,… n с определенной вероятностью.

Чистые стратегии игроков являются частными случаями смешанных, при этом

А1=(1,0,0,……0), А2=(0,1,0,……0) ….. Аm=(0,0,….0,1); В1=(1,0,0,……0), В2=(0,1,0,……0) ….. Вn=(0,0,….0,1);

Тогда смешанные стратегии можно представить в виде

m

P Ai pi , Ai - базисные векторы

i 1

Проанализируем структуру множества смешанных стратегий. Пусть у игрока А есть две чистые стратегии.

Для трех чистых стратегий имеем 2-мерный симплекс смешанных стратегий – треугольник с вершинами (1,0,0), (0,1,0), (0,0,1) (концы векторов P принадлежат треугольнику) и т.д.

37

Определение. Пара (P, Q) – образует исход игры (или игровую ситуацию). В которой выигрыш игрока A, равный aij , достигается с вероятностью piqj. H(P,Q) есть математическое ожидание выигрыша

(средний выигрыш) при избранных стратегиях игроков H(P, Q) M(pi , aij, qi ) piai jq j -

Пример. Пусть задана платежная матрица и стратегии игроков:

относительно смешанных стратегий Q игрока B. (SB - множество смешанных стратегий игрока B.)

38

P : (P) max (P) V неравентво (*) доказано

страт. P

Докажем, что V V : Для произвольных стратегий P и Q имеем:

(P) min H(P, Q) H(P, Q) max H(P, Q) (Q)

Определение. Если V V , то игра имеет цену в смешанных стратегиях => Максиминная и минимаксная стратегии тогда являются оптимальными.

Теорема. (Основная теорема антагонистических игр.) Для любой матричной игры существует решение в смешанных стратегиях ( V V , минимаксные стратегии оптимальны).

Без доказательства.

Тема 3. Лекция 9. Антагонистические игры. Критерии и свойства оптимальных стратегий.

В предыдущей лекции оптимальные стратегии P0 и Q0 соответственно игроков А и В определились в виде упорядоченной пары (P0,Q0), образующей ситуацию, в которой достигается равенство V=α(P0)= β(Q0)=H(P0,Q0). В следующей теореме в терминах цены игры V, функции выигрыша Н и множеств смешанных стратегий формулируются простые категории (необходимые и достаточные условия) оптимальных стратегий каждого из игроков.

Теорема 1. Пусть V — цена игры, H(P0,Q0) — функция выигрыша, SA и SB— множество смешанных стратегий А и В.

1. Для того чтобы стратегия P0 игрока А была оптимальной необходимо и достаточно, чтобы выполнялось неравенство

для любого Р SА, т.е. выбор игроком В одной из своих оптимальных стратегий Q0 гарантирует ему проигрыш не больший цены V, при любой стратеги Р игрока А.

Но цена игры V равна нижней цене игры V , по определению которой,

40