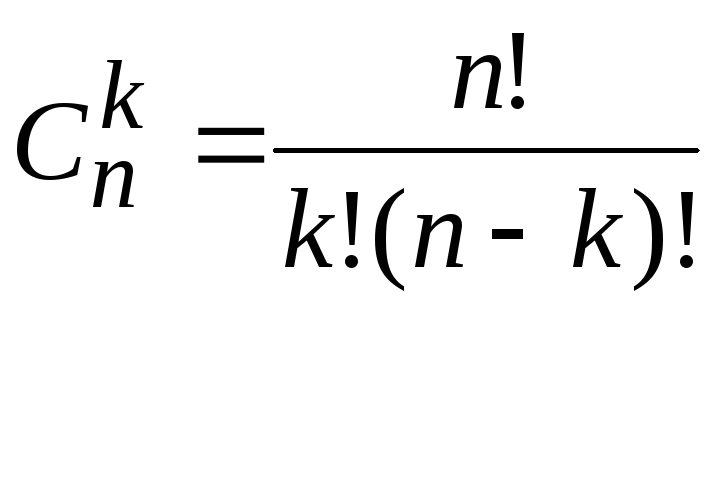1.1. Общие правила комбинаторики
Для успешного решения задач с использованием классического определения вероятности необходимо знать основные правила и формулы комбинаторики.
Комбинаторика – это раздел математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным правилам, можно составить из заданных объектов.
Основные правила комбинаторики: правило суммы и правило произведения.
|
Правила комбинаторики |
Пример |
|
Правило суммы | |
|
Если из некоторого конечного множества объект А можно выбрать m способами, о |
Сколькими способами можно выбрать одну четную или одну нечетную цифру из числа 145 678. Решение: В числе 145 678 три четные цифры и три нечетные. Четные цифры можно выбрать 3 способами, нечетные – тоже 3 способами. Четную или нечетную цифры: 3+3=6 способами. |
|
Если из некоторого конечного множества 1-й объект можно выбрать k1 способами, 2-й объект можно выбрать k2 способами, ……………………………………………, n-й объект можно выбрать kn способами то выбор или 1-го, или 2-го,…, или n-го объекта (любого из объектов) можно осуществить k1+k2+…+kn способами |
Сколько существует способов выбора одного карандаша из коробки, содержащей 5 красных, 7 синих, 3 зеленых карандаша? Решение: Красный карандаш можно выбрать 5 способами, синий – 7 способами, зеленый – 3 способами. Красный или синий или зеленый карандаш можно выбрать: 5+7+3=15 способами |
|
Правило произведения | |
|
Если из некоторого конечного множества объект А можно выбрать m способами, объект В можно выбрать способами, то выбор пары А и В в указанном порядке можно осуществить m |
Сколькими способами можно выбрать одну четную и одну нечетную цифру из числа 145 678. Решение: В числе 145 678 три четные цифры и три нечетные. Четные цифру можно выбрать 3 способами, нечетные – тоже 3 способами. Четную и нечетную цифру: 3∙3=9 способами
|
|
Если из некоторого конечного множества 1-й объект можно выбрать k1 способами, 2-й объект можно выбрать k2 способами, ……………………………………………, n-й объект можно выбрать kn способами то выбор и 1-го, и 2-го,…, и n-го объектов (всех n объектов) можно осуществить k1∙k2 ∙…∙kn способами |
В столовой имеются 4 первых блюда, 5 вторых и 3 третьих. Сколькими способами можно составить из них полноценный обед? Решение: Первое блюдо можно выбрать 4 способами, второе – 5 способами, третье – 3 способами. Выбор обеда из трех блюд: первое и второе и третье можно выбрать: 4∙5∙3=60 способами |
бъектВ
можно выбрать n
способами,
то выбор А
или
В
можно осуществить m+n
способами
∙n
способами
Основные комбинаторные конфигурации: размещения, сочетания, перестановки
Обычно в комбинаторике рассматривается идеализированный эксперимент по выбору k элементов из n. При этом элементы:
а) не возвращаются обратно (схема выбора без возвращений);
б) возвращаются обратно (схема выбора с возвращением).
|
Схема выбора без возвращений | |||
|
Размещение из n элементов по k элементам |
Перестановка из n элементов |
Сочетание из n элементов по k элементам | |
|
Схема выбора c возвращением | |||
|
Размещение из n элементов по k элементам с повторениями |
Сочетание из n элементов по k элементам с повторениями | ||
|
Размещения | ||
|
Размещением из n элементов по k элементам называют упорядоченный набор из k элементов, принадлежащих n-элементному множеству |
Размещения отличны друг от друга или порядком элементов, или их составом |
Число размещений из n элементов по k элементам обозначается и вычисляется по формуле:
|
|
Перестановки | ||
|
Перестановкой из n элементов называют размещение из n элементов по n |
Перестановки отличны друг от друга порядком элементов |
Число перестановок из n элементов обозначается и вычисляется по формуле
Рn=n!
|
|
Сочетания | ||
|
Сочетанием из n элементов по k элементам называют любой набор из k элементов, принадлежащих n-элементному множеству |
Сочетания отличны друг от друга только составом элементов |
Число сочетаний из n элементов по k элементам обозначается и вычисляется по формуле
|
