Общая теория статистики Назаров

.

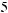
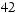
В скобках указаны tнабл(bj) = tj — расчетные значения t критерия для проверки гипотезы о значимости коэффициента регрессии

H0 : bj = 0, j = 1, 2, 3, 4, 5. Критическое значение tкр = 1,76 найдено по таблице t распределения при уровне значимости α = 0,1 и числе

степеней свободы v = 14. Из уравнения следует, что статистичес ки значимым является коэффициент регрессии только при x4, так как |t4| = 2,90 > tкр = 1,76. Не поддаются экономической интерпрета ции отрицательные значения коэффициентов регрессии при x1 и x5, которые свидетельствуют о том, что повышение насыщенности сельского хозяйства колесными тракторами (x1) и химическими средствами оздоровления растений (x5) отрицательно сказывается на урожайности. Таким образом, полученное уравнение регрессии неприемлемо.

После реализации алгоритма пошагового регрессионного ана лиза с исключением переменных и учетом того, что в уравнение должна войти только одна из трех тесно связанных переменных (x1, x2 или x3), получаем окончательное уравнение регрессии

.

Уравнение значимо при α = 0,05, так как F = 266 > Fкр = 3,20, найденного по таблице F распределения при α = 0,05, v = 3 и v = 17. Значимы и коэффициенты регрессии β1 и β4, так как |tj| > tкр = 2,11 (при α = 0,05, v = 17). Коэффициент регрессии β1 следует признать значимым (β1 ≠ 0) из экономических соображений; при этом t1 = 2,09 лишь незначительно меньше tkp = 2,11. В случае если α = 0,1, tkp = 1,74 и коэффициент регрессии β1 статистически значим.

Из уравнения регрессии следует, что увеличение на единицу чис ла тракторов на 100 га пашни приводит к росту урожайности зер

показывают, что при увеличении показателей x1 и x4 на 1% урожай ность зерновых повышается соответственно на 0,068% и 0,161%.

Множественный коэффициент детерминации ry2 = 0,469 свиде тельствует о том, что только 46,9% вариации урожайности объяс няется вошедшими в модель показателями (x1 и x4), т.е. насыщен

ностью растениеводства тракторами и удобрениями. Остальная часть вариации обусловлена действием неучтенных факторов (x2, x3, x5, погодными условиями и др.). Средняя относительная ошиб ка аппроксимации δ = 10,5% свидетельствует об адекватности мо дели, так же как и величина остаточной дисперсии s2 = 1,97.

15.4. Экономико?математические методы прогнозирования социально?экономических явлений

Трендовые модели прогнозирования. Статистические наблюдения в социально экономических исследованиях обычно проводятся регулярно через равные отрезки времени и представляются в виде временных рядов xt, где t = 1, 2 … n. В качестве инструмента стати стического прогнозирования временны´ х рядов служат трендовые регрессионные модели, параметры которых оцениваются по име ющейся статистической базе, а затем основные тенденции (трен ды) экстраполируются на заданный интервал времени.

Методология статистического прогнозирования предполагает построение и испытание многих моделей для каждого временно´ го ряда, сравнение их на основе статистических критериев и отбор наилучших из них для прогнозирования.

При моделировании сезонных явлений в статистических иссле дованиях различают два типа колебаний: мультипликативные и ад дитивные. В мультипликативном случае размах сезонных колеба ний изменяется во времени пропорционально уровню тренда и отражается в статистической модели множителем. При аддитивной сезонности предполагается, что амплитуда сезонных отклонений постоянна и не зависит от уровня тренда, а сами колебания пред ставлены в модели слагаемым.

Основой большинства методов прогнозирования является экст раполяция, связанная с распространением закономерностей, связей и соотношений, действующих в изучаемом периоде, за его пределы или, в более широком смысле слова, это получение представлений о будущем на основе информации, относящейся к прошлому и насто ящему.

Наиболее известны и широко применяются трендовые и адап тивные методы прогнозирования. Среди последних можно выде

15.4. Экономико?математические методы прогнозирования... 373

лить такие, как методы авторегрессии и скользящего среднего (Бокса — Дженкинса и адаптивной фильтрации), методы экспо ненциального сглаживания (модели Хольта, Брауна и экспонен циальной средней) и др.

Для оценки качества исследуемой модели прогноза использует ся несколько статистических критериев.

Наиболее распространенными критериями являются следую щие.

Относительная ошибка аппроксимации:

где et = xt − xt — ошибка прогноза;

xt — фактическое значение показателя; xt — прогнозируемое значение.

Данный показатель используется в случае сравнения точности прогнозов по нескольким моделям. При этом считают, что точность модели является высокой, когда δ < 10%, хорошей — при δ = (10— 20)% и удовлетворительной — при δ = (20—50)%.

Средняя квадратическая ошибка:

где k — число оцениваемых коэффициентов уравнения.

Наряду с точечным в практике прогнозирования широко исполь зуют интервальный прогноз. При этом доверительный интервал чаще всего задается неравенствами

где tα — табличное значение, определяемое по t распределению Стьюдента при уровне значимости α и числе степеней свободы n – k.

В литературе представлено большое число математико статис тических моделей для адекватного описания разнообразных тен денций временны´ х рядов.

К наиболее распространенным видам трендовых моделей, ха рактеризующих монотонное возрастание или убывание исследуе мого явления, относятся:

xt = b0 + b1t,

xt = b0 + b1t + b2t 2, xt = b0eb1t,

xt = b0tb1, xt = b0 + bt1 , xt = b0 − b1et ,

xt = b0 + b1ln(t).

Правильно выбранная модель должна соответствовать характе ру изменений тенденции исследуемого явления. При этом величи на et должна носить случайный характер с нулевой средней.

Кроме того, ошибки аппроксимации et должны быть независи мы между собой и подчиняться нормальному закону распределения et N(0, σ). Независимость ошибок et, т.е. отсутствие автокорреля ции остатков, обычно проверяется по критерию Дарбина — Уотсо на, основанного на статистике:

где et = xt − xt .

Если отклонения не коррелированны, то величина DW прибли зительно равна двум. При наличии положительной автокорреля ции 0 ≤ DW < 2, а отрицательной 2 < DW ≤ 4.

О коррелированности остатков можно также судить по корре лограмме для отклонений от тренда, которая представляет собой графики функции относительно τ коэффициента автокорреляции, который вычисляется по формуле:

где τ = 0, 1, 2 ... .

После выбора наиболее подходящей аналитической функции для тренда его используют для прогнозирования на основе экстрапо ляции на заданное число временны´ х интервалов.

Рассмотрим задачу сглаживания сезонных колебаний исходя из ряда Vt = xt − xt , где xt — значение исходного временного ряда в

15.4. Экономико?математические методы прогнозирования... 375

момент t, а xt — оценка соответствующего значения тренда (t = 1, 2 ... n).

Так как сезонные колебания представляют собой циклический, повторяющийся во времени процесс, то в качестве сглаживающих функций используется гармонический ряд (ряд Фурье) следующе го вида:

Оценки параметров αi и βi в модели определяют из выражений

где k = n/2 — максимально допустимое число гармоник;

ωi = 2πi/n — угловая частота i й гармоники (i = 1, 2 ... m).

Пусть m — число гармоник, используемых для сглаживания се зонных колебаний (m < k). Тогда оценка гармонического ряда име ет вид

а расчетные значения временного ряда исходного показателя оп ределяются по формуле

Адаптивные методы прогнозирования. При использовании трен довых моделей в прогнозировании обычно предполагается, что ос новные факторы и тенденции прошлого периода сохраняются на период прогноза или что можно обосновать и учесть направление их изменений в перспективе. Однако в настоящее время, когда про исходит структурная перестройка экономики, социально эконо

376 Глава 15. Cтатистическое изучение взаимосвязи...

мические процессы даже на макроуровне становятся очень дина мичными. В этой связи исследователь часто имеет дело с новыми явлениями и с короткими временными рядами. При этом устарев шие данные при моделировании часто оказываются бесполезными и даже вредными. Таким образом, возникает необходимость стро ить модели, опираясь в основном на малое количество самых све жих данных, наделяя модели адаптивными свойствами.

Важную роль в деле совершенствования прогнозирования дол жны сыграть адаптивные методы, цель которых заключается в по строении самонастраивающихся моделей, способных учитывать информационную ценность различных членов временно´ го ряда и давать достаточно точные оценки будущих членов данного ряда. Адаптивные модели достаточно гибки, однако на их универсаль ность, пригодность для любого временно´ го ряда рассчитывать не приходится.

При построении конкретных моделей необходимо учитывать наиболее вероятные закономерности развития реального процес са. Исследователь должен закладывать в модель только те адаптив ные свойства, которые необходимы для слежения за реальным про цессом с заданной точностью.

В основе адаптивного направления лежит простейшая модель экспоненциального сглаживания, обобщение которой привело к появлению целого семейства адаптивных моделей. Простейшая адаптивная модель основывается на вычислении экспоненциаль но взвешенной скользящей средней.

Экспоненциальное сглаживание исходного временного ряда xt

где St — значение экспоненциальной средней в момент t, а St–1 — в мо мент t–1;

α — параметр сглаживания, адаптации, α = const, 0 < α < 1; β = 1– α.

Выражение экспоненциальной средней можно представить в

В формуле (15.39) экспоненциальная средняя в момент t выра жена как сумма экспоненциальной средней предшествующего мо мента St – 1 и доли α отклонения текущего наблюдения xt от экспо ненциальной средней St – 1 момента t – 1.

15.4. Экономико?математические методы прогнозирования... 377

Последовательно используя рекуррентное соотношение, мож но выразить экспоненциальную среднюю St через все предшеству ющие значения временного ряда:

t−1

St = αxt + αβxt −1 + β2St −2 = ... = α ∑ βi xt −i + βtS0, (15.40)

i=0

где S0 — величина, характеризующая начальные условия для первого при менения формулы средней, при t = 1.

Так как β = (1 – α) < 1, то при t → ∞ βt → 0. Отсюда следует, что

t−1

St = α ∑ βi xt −i , (15.41)

i=0

т.е. величина St оказывается взвешенной суммой всех членов ряда. При этом веса изменяются экспоненциально в зависимости от давности наблюдения, откуда и название St — экспоненциальная средняя.

Из формулы (15.41) следует, что увеличение веса более свежих наблюдений может быть достигнуто повышением α. В то же время для сглаживания случайных колебаний временно´ го ряда xt величи ну α нужно уменьшить. Два названных требования находятся в про тиворечии и на практике при выборе α исходят из компромиссно го решения.

Экспоненциальное сглаживание является простейшим видом самообучающейся модели с параметром адаптации α. Разработано несколько вариантов адаптивных моделей, которые используют процедуру экспоненциального сглаживания и позволяют учесть наличие у временного ряда xt тенденций и сезонных колебаний. Рассмотрим некоторые из таких моделей.

Пример. На основании данных (в млн руб.) объема продаж тор гового дома за n = 12 месяцев (табл. 15.3) необходимо построить регрессионную модель зависимости объема продаж от времени.

Таблица 15.3

Данные объема продаж, млн руб.

378 Глава 15. Cтатистическое изучение взаимосвязи...

Окончание табл. 15.3

Первоначально аппроксимируем временной ряд линейным урав нением регрессии вида yt = β0 + β1t.

Оценка уравнения регрессии, найденная с помощью метода наи меньших квадратов, имеет вид:

yt = 230+ 11,15t .

(5,84)

В скобках указаны оценки среднеквадратических отклонений коэффициентов уравнения sb j (j = 0,1). Уравнение значимо и содер жит все значимые по t критерию коэффициенты βj. Критическое значение tkp= 2,23, найденное при α = 0,05 и v = n – 2 = 10, по табли

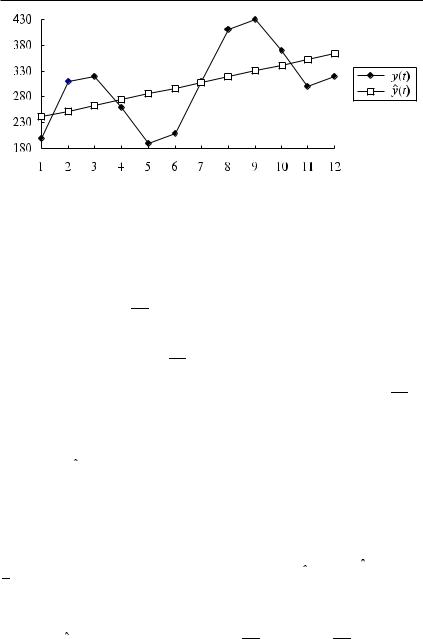
Статистические характеристики уравнения (s = 69,88; R2 = 0,27 и DW = 1,01) свидетельствуют о наличии положительной коррели рованности случайных остатков и о недостаточно хороших аппрок симирующих свойствах модели. Анализируя рис. 15.4, где представ лены графики yt и yt , можно предположить наличие периодической (сезонной) составляющей временного ряда.

Для описания сезонных колебаний, представляющих собой цик лический повторяющийся во времени процесс, может быть исполь зован гармонический ряд (ряд Фурье) вида:

j =1, 2 ... k — номер гармоники; εt — случайная ошибка.

15.4. Экономико?математические методы прогнозирования... 379

Рис. 15.4. Временной ряд объема продаж yt

Из рис. 15.4 видно, что обследуемый временной диапазон n = 12 вмещает в себя два полных периода циклических колебаний ана лизируемого показателя. Отсюда можно предположить, что для адекватного описания vt достаточно второй гармоники (j = 2) с уг

ловой частотой ω2 = 2π 2.

12 Первоначально включим в модель объема продаж две гармоники

с угловыми частотами ω1 = 2π 1 и ω2. Будем строить линейное урав 12

нение регрессии относительно следующих переменных: t, sin 2π t,

Уравнение содержит два незначимых коэффициента регрессии, относящихся к 1 й гармонике (tkp = 2,447 при α = 0,05 и ν = 6). Ста тистические характеристики уравнения равны: s = 3,32; R2 = 0,999; δ = 0,55% и DW = 3,32. После реализации процедур в качестве окон чательного было выбрано уравнение регрессии вида:

Все входящие в уравнение коэффициенты значимы, т.е. βj ≠ 0 (j = 0, 1, 2, 3). Как видно из полученного уравнения, расчетные зна чения |tj| больше критического значения tkp = 2,306, найденного по таблице t распределения при α = 0,05 и ν = 8, из чего следует, что гипотеза H0 : βj = 0 отвергается с вероятностью ошибки α = 0,05.

Уравнение характеризуется: остаточным среднеквадратическим отклонением s = 3,32; множественным коэффициентом детерми нации R2 = 0,999; средней относительной ошибкой аппроксимации δ = 0,75% и статистикой Дарбина — Уотсона DW = 3,025, что свиде тельствует об адекватности модели. Полученные характеристики особенно впечатляют при их сравнении с аналогичными парамет рами линейного тренда.

Адаптивная полиномиальная модель первого порядка. Рассмотрим алгоритм экспоненциального сглаживания, предполагающий на личие у временно´го ряда xt линейного тренда. В основе модели лежит гипотеза о том, что прогноз может быть получен по уравнению

где xτ (t) — прогнозируемое значение временно´ го ряда на момент (t + τ); a1.t , τa2.t — оценки адаптивных коэффициентов полинома первого по

рядка в момент t;

τ — величина упреждения.

Экспоненциальные средние 1 го и 2 го порядков для модели имеют вид

где β = 1 – α, а оценка модельного значения ряда с периодом упреждения τ равна

Для определения начальных условий первоначально по данным временно´ го ряда xt находим методом наименьших квадратов оцен ки линейного тренда

и принимаем a0.1 = a1 и a0.2 = a2. Тогда начальные условия определя ются как