Общая теория статистики Назаров

Вариант данного индекса был предложен Г. Пааше. С помощью индекса цен по формуле Пааше определяется изменение стоимос ти продукции в отчетном периоде по сравнению с базисным в ре зультате изменения цен.

Агрегатный (сводный) индекс цен будет следующим:

или 50,7%.

Цены на овощную продукцию снизились на 49,3% в отчетном периоде (июнь) по сравнению с базисным (апрель).

Абсолютное изменение всей стоимости овощной продукции за счет изменения цен составило: 2 685 245,8 руб. (Σp1q1 – Σp0q1 = = 2 762 111,75 – 5 447 357,5).

Сводный индекс физического объема реализации показывает изменение количества реализованной продукции (проданных то варов), где индексируемая величина — количество реализованной продукции, а веса — цены базисного периода:

или 194,2%.

Объем реализованной овощной продукции увеличился в отчет ном периоде по сравнению с базисным в 1,94 раза, или на 94,2%.

Между рассчитанными индексами (стоимости продукции, цен и количества реализованной продукции) существует следующая взаимосвязь:

Ipq = Ip Iq.

0,985 = 0,507 1,942.

Следовательно, все расчеты произведены правильно (0,985 = 0,985). На величину индекса стоимости продукции (товарооборота)

оказывает влияние два фактора: цены и количество реализованной продукции. Рассмотрим влияние каждого из факторов в отдельно сти.

Общее снижение стоимости продукции составило – 42 563,25 руб., в том числе за счет:

а) снижения цен:

Σp1q1 – Σp0q1 = 2 762 111,75 – 5 447 357,5 = –2 685 245,75 руб.;

б) увеличения количества реализованной продукции:

Σq1p0 – Σq0p0 = 5 447 357,5 – 2 804 675 = 2 642 682,5 руб.

Проверим взаимосвязь исчисленных показателей:

–2 685 245,75 + 2 642 682,5 = –42 563,25.

13.3. Средние индексы из индивидуальных. Средний арифметический и средний гармонический индексы

Если имеющиеся исходные данные не дают возможности про извести индексный анализ в агрегатной форме, то применяется форма средних индексов из индивидуальных.

Как правило, средние индексы рассчитываются с использова нием двух форм средних — арифметической и гармонической — и соответственно называются средним индексом в форме среднего арифметического и средним индексом в форме среднего гармони ческого индекса.

Средний арифметический индекс физического объема продук ции рассчитывается по следующей формуле:

Так как , тогда q1 = iq q0, формула этого индекса преобразу ется в формулу

Пример 2. Рассчитаем средний арифметический индекс, исполь зуя данные примера 1, исходя из предположения, что отсутствуют данные о товарообороте текущего периода (табл. 13.2).

Чтобы найти средний арифметический индекс, необходимо ис пользовать формулу индивидуального объема продукции.

Индивидуальный индекс физического объема огурцов будет следующим:

По аналогии рассчитываются индивидуальные индексы поми доров и перца (см. гр. 4 табл. 13.2). Полученные значения подста вим в формулу среднего арифметического индекса:

или 194,2%.

Как и следовало ожидать, значения агрегатного и среднего ариф метического индексов совпали.

Среднегармонический индекс рассчитывается в том случае, ког да известны данные отчетного периода, а базисные данные отсут ствуют, и известно изменение индивидуального индекса.

13.4. Индексы переменного и постоянного состава

При анализе динамики среднего показателя возникает необхо димость отразить воздействие двух факторов, влияющих на его ве личину:

1) изменение значения показателя у отдельных групп единиц совокупности;

2) изменение структуры совокупности.

Для этого используются индексы переменного состава.

Индекс переменного состава рассчитывается по формуле

Индекс постоянного состава (Iп.с) характеризует изменение толь ко индексируемой величины при фиксированной структуре сово купности.

В качестве веса индекса постоянного состава должна быть взята структура отчетного периода. Индекс постоянного (фиксирован ного) состава рассчитывается следующим образом:

Индекс структурных сдвигов (Iстр.сдв) характеризует влияние из менения структуры изучаемого явления на динамику среднего по

казателя. Уровень показателя берется по базисному периоду. Ин декс влияния структурных сдвигов определяется по формуле

Система взаимосвязанных индексов переменного, постоянного состава и структурных сдвигов при анализе динамики средних по казателей имеет следующий вид:

Iпер.с = Iп.с Iстр.сдв

Пример 3. Рассчитаем индексы переменного, постоянного соста ва и влияния структурных сдвигов, используя данные примера 1.

Общие изменения цен с учетом количества реализованной про дукции покажет индекс переменного состава:

Следовательно, средняя цена реализации овощной продукции снизилась в отчетном периоде по сравнению с базисным на 48,8%.

Рассмотрим, за счет каких факторов произошло это снижение цены.

Для этого определим индекс влияния структурных сдвигов на изменение средней цены:

p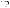 или 100,9%.

Таким образом, структурные сдвиги в реализации объема овощ ной продукции в данном магазине вызвали повышение средней цены в отчетном периоде на 0,9%.

Вместе с тем снижение цен на овощную продукцию в отчетном периоде оказало влияние на уровень средней цены. Для оценки влияния данного фактора определим индекс цен постоянного (фик сированного) состава:

Другими словами, в отчетном периоде цены на овощную про дукцию снизились на 49,3%.

Система взаимосвязанных индексов для анализа динамики сред ней цены будет следующей:

Jpпер.с = Jpп.с Jpстр.сдв .

В рассматриваемом периоде Jp = 0,5071 1,009 = 0,512. Проведенный анализ показывает, что снижение цен овощной

продукции на 48,8% обусловлено, с одной стороны, ростом на 0,9%

в результате структурных сдвигов в объеме реализации, а с другой — снижением в среднем на 49,3% цен отдельных видов овощной про дукции.

Контрольные вопросы и задания

1.Дайте понятие индексов и назовите их виды.

2.Как строятся индивидуальные и сводные (общие) индексы?

3.Какие существуют формы средних индексов из индивидуаль

ных?

4.В чем состоит различие в расчете индексов методом Пааше и Ласпейреса?

5.Что понимается под индексом переменного и постоянного состава? Какая между ними существует взаимосвязь?

Тесты

1. Что такое экономический индекс?

А. Отношение сравнительного уровня (более позднего) к уров ню, принятому за базу сравнения (более раннему).

Б. Средняя из модулей отклонений индивидуальных значений признака от средней величины.

В. Средний квадрат отклонений индивидуальных значений при знака от средней величины.

Г. Таблица, в которой представлены значения показателя за пос ледовательные периоды или на моменты времени.

Д. Относительная величина, которая характеризует применение исследуемого явления в момент t, в пространстве или по сравне нию с некоторым этапом.

Е. Частное от деления величины базисного абсолютного изме нения на число осредняемых отрезков времени от базисного до срав ниваемого периода.

2. Какие формы построения общих индексов используют в за висимости от цели исследования и наличия исходных данных?

А. Агрегатную.

Б. Логарифмическую. В. Средневзвешенную. Г. Кумулятивную.

Д. Правильного ответа нет.

318 Глава 13. Индексы

7. Как можно охарактеризовать индекс переменного состава? А. Представляет собой отношение двух взвешенных средних ве

личин с переменными весами, характеризующими изменение ин дексируемого (осредненного) показателя.

Б. Учитывает изменение только индексируемой величины, по казывает средний размер изменения изучаемого показателя у еди ницы совместимости.

В. Характеризует влияние и изменения структуры изучаемого явления на динамику среднего уровня индексируемого показа теля.

8. Каким образом рассчитывается индекс цен постоянного со става?

А.∑ p1q1 . ∑ p1q1

Г.∑ p1q1 .

∑p1q1 ip

9. Какие средневзвешенные индексы применяются в статисти ческой практике?

А. Среднеарифметический. Б. Среднехронологический. В. Среднегармонический.

Г. Среднеквадратический.

10. Для расчета сводного индекса физического объема товаро оборота можно использовать среднюю арифметическую форму. Какой вид тогда примет индекс?

А.∑ q1 p0 .

∑q0 p0

Б.∑ iqq0 p0 .

∑q0 p0

В.∑ q1t0 .

∑q0t0

Г.∑ q1z0 .

∑q0 z0

Д. ∑ q1 p0 .

∑ i1 q1 p0

q

11. Как рассчитывается среднегармонический индекс цен?

А.∑ q1 p0 .

∑p1q1 ip

В.∑ p1q1 .

∑p0q0

Г. ∑ q1 p1 : ∑ q0 p1 .

∑T1 ∑ T0

Д. i1 p1.

p

12. Как определяется индекс производительности труда по тру доемкости (индекс С.Г. Струмилина)?

А.∑ itT1 .

∑T1

Д. Правильного ответа нет.