Задача 8

Данные о выпуске продукции плодоконсервным заводом за отчетный период:

Вид продукции	Вес банки, г	Количество банок, тыс. шт
Повидло	1000	100
Джем	650	190
Конфитюр	370	80

Определите:

1) общий объем произведенной продукции, приняв в качестве условной единицы банку весом 440 г;

2) структуру выпуска продукции по видам;

3) относительную величину выполнения задания по выпуску продукции, если размер задания составлял 480 туб. (тысяч условных банок).

Решение

1. Для определения коэффициента пересчета (Кп) вес банки по каждому виду продукции следует разделить на эталонное значение (440 г.). Занесем результаты расчетов в таблицу.

Пересчитаем объем продукции в натуральном выражении в условно-натуральные единицы – условные банки. Занесем результаты расчетов в таблицу.

Q_y = 440г – условная единица

Вид продукции	Вес банки, г	Количество банок, тыс. шт	kn	Qy
Повидло	1000	100	1000/440=2,27	2,27*100=227
Джем	650	190	650/440=1,48	1,48*190=281,2
Конфитюр	370	80	370/440=0,84	0,84*80=67,2
Общий объем произведенной продукции					575,4

2. 

Вид продукции	Количество банок, тыс. шт	Структура, %
Повидло	100	27,03%
Джем	190	51,35%
Конфитюр	80	21,62%
Итого	370	100%

3. Относительная величина задания определяется по формуле:

Задача 24

С целью изучения производительности труда работников предприятия произведено 10%-ное выборочное обследование (по методу механического отбора). Результаты представлены следующими данными:

Группы работников по выработке изделий за смену, шт.	Число работников, чел.
до 30	5
30-40	25
40-50	50
50-60	12
60 и более	8
Итого	100

Определите:

1) среднюю выработку изделий за смену одним работником;

2) дисперсию и среднее квадратическое отклонение;

3) коэффициент вариации;

4) с вероятностью 0,954 предельную ошибку выборки, а также интервал, в котором находится удельный вес всех работников предприятия, производящих за смену более 50 изделий.

Сделайте выводы.

Решение

Группы работников по выработке изделий за смену, шт.	Число работников, чел. (f)	Середина интервалов (x)	x*f
до 30	5	25	125	(-19)2=361	1805
30-40	25	35	875	(-9)2=81	2025
40-50	50	45	2250	12=1	50
50-60	12	55	660	112=121	1452
60 и более	8	65	520	212=441	3528
Итого	100		4430		8860

1. Найдем среднюю выработку изделий за смену по формуле средней арифметической взвешенной

где - середина интервала;

f_i. – число работников в каждом интервале.

- средняя выработка одного рабочего

2. Дисперсию признака определим по формуле:

.

(дисперсия)

Среднее квадратическое отклонение:

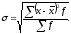
(среднее квадратичное отклонение)

3. Коэффициент вариации (V) вычисляется процентным отношением среднего квадратического отклонения к средней арифметической:

- совокупность количественно однородная

4. По условию задачи было произведено 10%-ное выборочное обследование (по методу механического отбора). Поэтому численность генеральной совокупности N = 1000 чел.

Определим удельный вес работников предприятия, производящих более 50 изделий:

или 20 %.

При заданной вероятности P = 0,954 коэффициент доверия t = 2. Вычислим предельную ошибку выборки для генеральной доли:

Определим пределы удельного веса работников предприятия, производящих более 50 изделий:

0,2 – 0,076 р 0,2 + 0,076,

0,124 р 0,276 или 12,4 %  р  27,6 %.

Вывод: с вероятностью 0,954 можно гарантировать, что в генеральной совокупности (N = 1000 чел.) доля работников предприятия, производящих более 50 изделий будет находиться в пределах от 12,4 до 27,6 %.