
Лабораторная работа №1
Программа линейных алгоритмов
|
Вариант 1 а) x= 4,75b= -15,66c= 3,36 б) t, r, z в)
Q = P
= cos M =
|
Вариант 2 а) а = -14,б75 b= 18,65 б) , , в) X
=
Q
=
R =
|
|
Вариант 3 а) x= -10,3y= 4,85z= -3,37 б) , p, r. в)
T =
Q = Sin2Cos2p – r2eSiny+Cosx
|
Вариант 4 а) x= 7,14y= 37,4z= 0,5 б) , , . в)
A =
B =
|
|
Вариант 5 а) x= -7,87y= 77,8a= -4,6 б) , , t.
в)
P =
M =
|
Вариант 6 а) = -14б7= 4б37= 0б385 б) x,y,z. в)
A =
B =
|
|
Вариант 7 а) x= 16,51a= -4,02d= 0,07 б) y, z, q. в)
P =
|
Вариант 8 а) a= -0,65b= 4,78c= -12,65 б) x, y, z. в)
P =
T =
|
|
Вариант 9 а) t= 5,4r= -6,15z= 0,3 б) x, b, c. в)
Q =
P
=
M =
|
Вариант 10 а) = 7,514= 6,18= -1,05 б) a,b. в)
X =
Q
=
R =
|
Лабораторная работа № 2
Программа разветвляющихся алгоритмов
|
Вариант 1
y
=
для r, a. |
Вариант 2 M=Cos2(Sin2x) +zex+z2; где
для y, r.
|
|
Вариант 3 P=Sin2(Cosxy) +e-xy– 2,65; где
для a, b
|
Вариант 4 Y
=
для b, a. |
|
Вариант 5 K= ( - 1)Cos3x– ( + 1)Sin2z; где
для r, a. |
Вариант 6 Т =
для r, x.
|
|
Вариант 7 Z=
x=
y=
для a, t. |
Вариант 8 T = a3 (z+ 2) (2z+ 1) –b+ 1 +z nz; где a
=
b
=
для x, z.
|
|
Вариант 9 Q=
x=
z=
для y, i. |
Вариант 10 T=Sin2(Cosx) +zex+1+y2+ 3; где x
=
z
=
для y, z |
Лабораторная работа № 3
Табулирование функции (сочетание цикла и разветвлений)
|
Вариант 1 Задание № 1 H
= y, x[ 0; 1 ]h= 0,2 |
Вариант 2 Задание № 1 P
=
y, x[0; 1] h = 0,2 |
|
Вариант 3 Задание № 1 Z=
t, x[2;4] h = 0,2 |
Вариант 4 Задание № 1 Y = t2 n (x2 + 1) - n (x + t);
t, x[1;2] h = 0,2 |
|
Вариант 5 Задание № 1 M
=
y; x[1;e] h = |
Вариант 6 Задание № 1 y
= n a, x[2;4] h = 0,2 |
|
Вариант 7 Задание № 1 P
= Sin2
+
y, x [1; 3] h = 0,2 |
Вариант 8 Задание № 1 y=
a,x[-4;4]h= 1,5 |
|
Вариант 9 Задание № 1 y=Sin2(x+5a) – 2aCosx2 a, x[-2; 14] h = 2 |
Вариант 10 Задание № 1 y=
t,x[1; 2]h= 0,25 |
Лабораторная работа № 4
|
Вариант 1 Найти максимум функции R= ;y=
x [0; 2] h = 0, 4 |
Вариант 2 Найти минимум функции Z=
x [0; 2] h = 0,4 |
|
Вариант 3 Найти минимум функции Y=
x [0; 1] h = 0,2 |
Вариант 4 Найти максимум функции Y=
x [0; 1] h = 0,1 |
|
Вариант 5 Найти максимум функции Z=
x [-1; 1] h = 0,1 |
Вариант 6 Найти максимум функции
Z=
x [1; 2] h = 0,2 |
|
Вариант 7 Найти минимум функции Т =
x [1; 4] h = 0,5 |
Вариант 8 Найти максимум функции Z= x [1; 4] h = 0,5 |
|
Вариант 9 Найти минимум функции Y=
x [0; 1] h = 0,2 |
Вариант 10 Найти максимум функции Q=
x [-П; П] h = 0,5 |

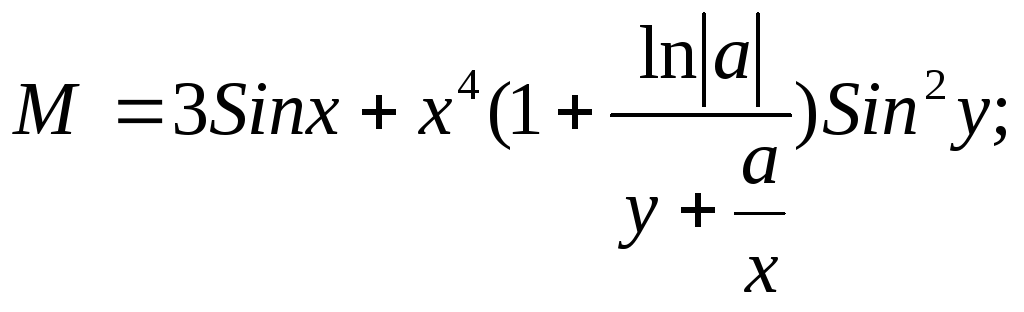 где
где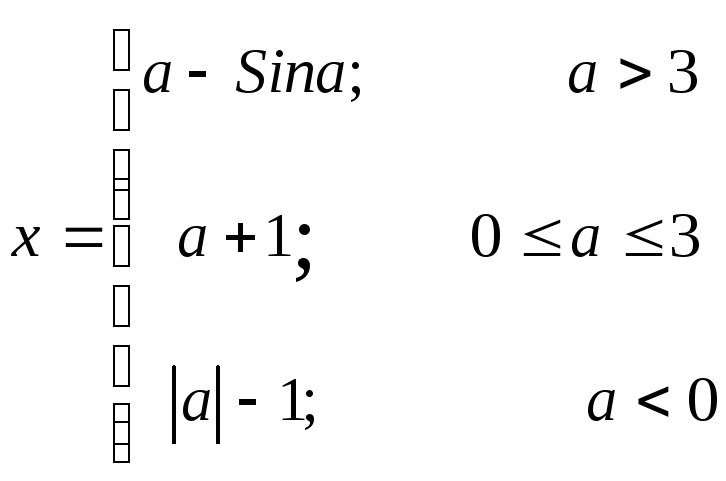
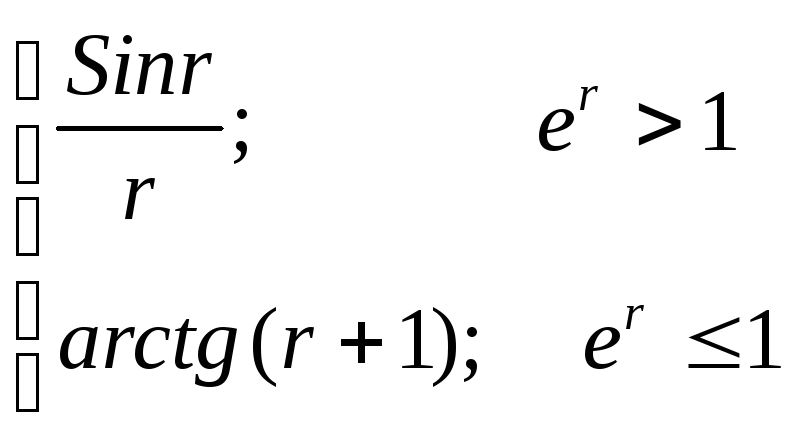
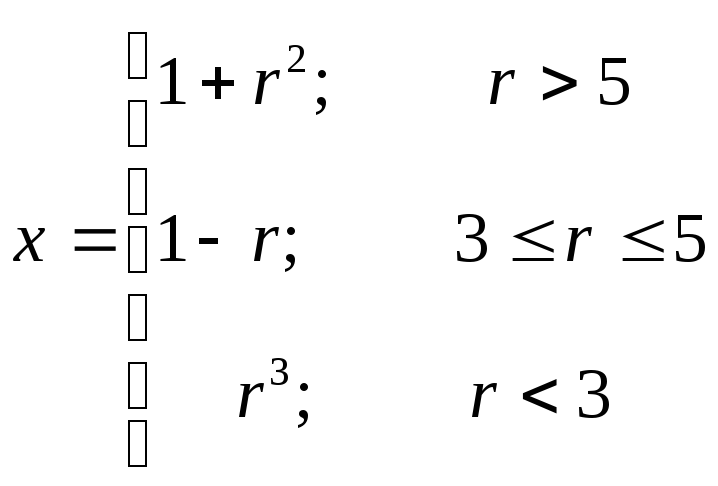
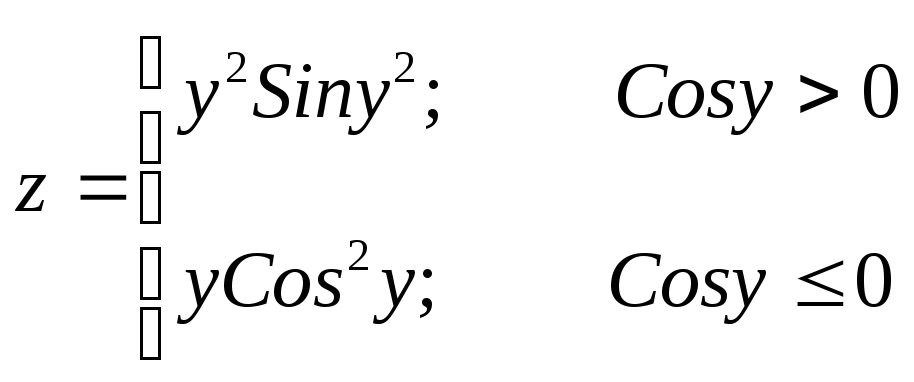
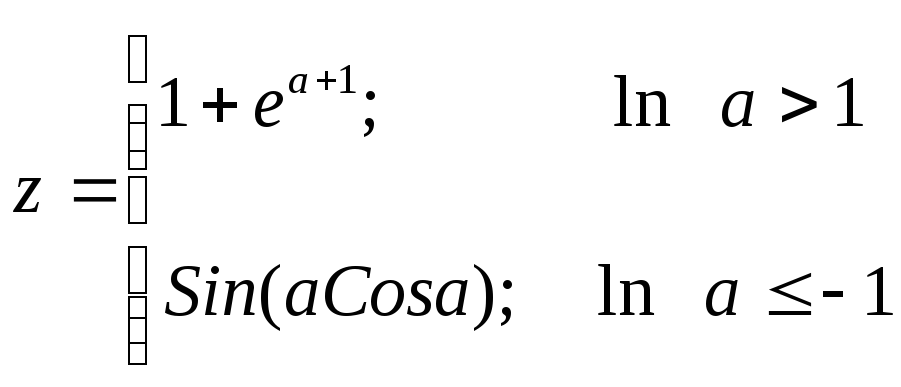
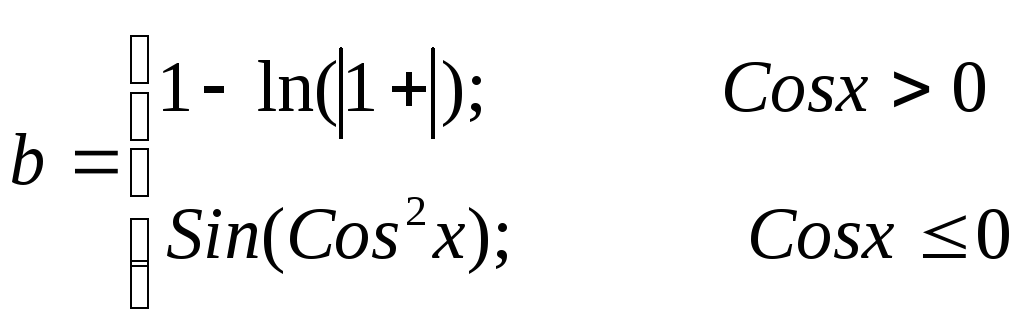
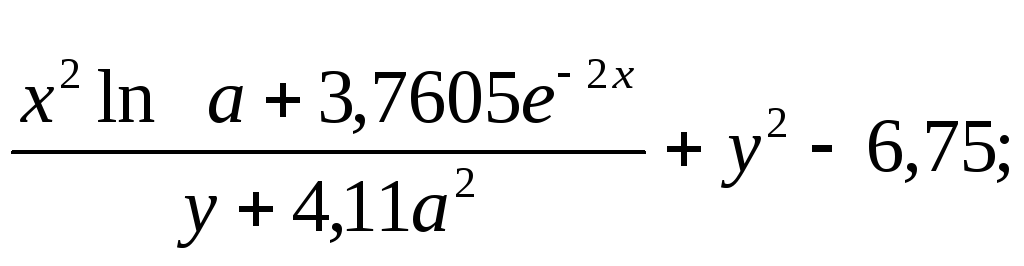 где
где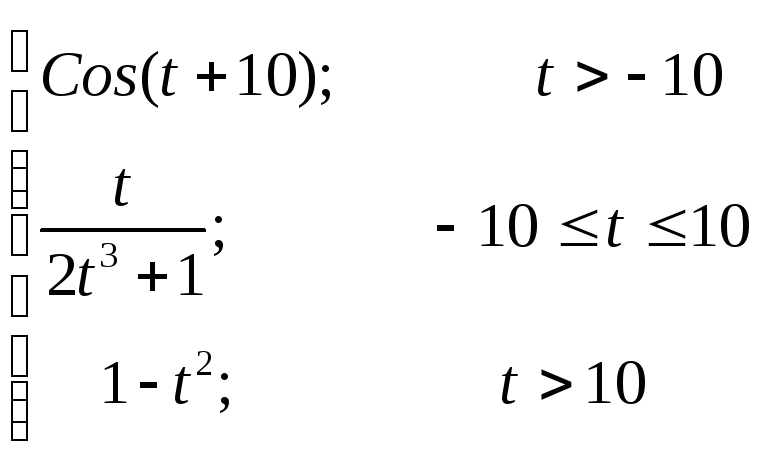
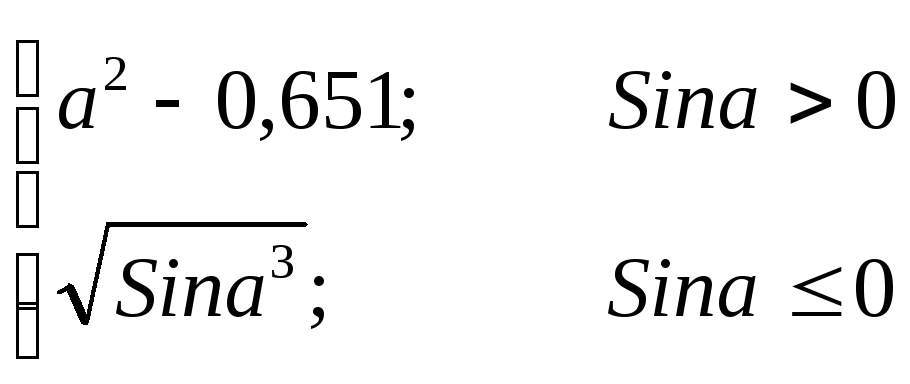
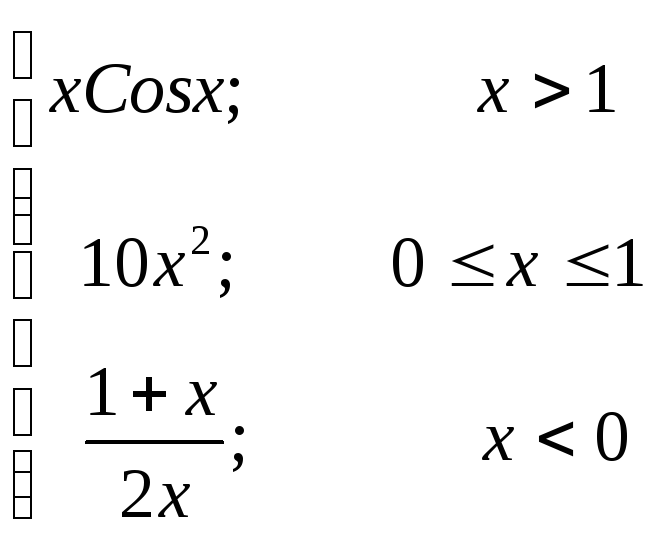
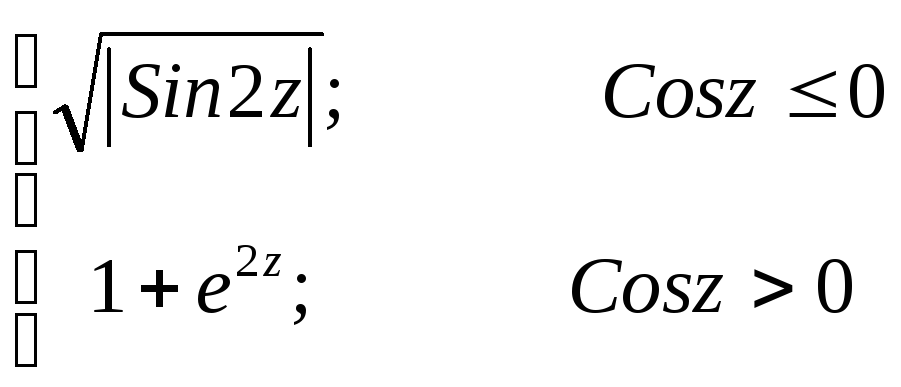
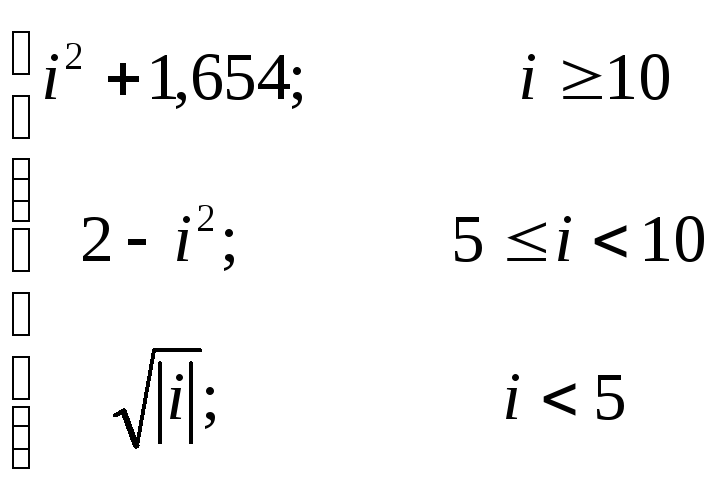
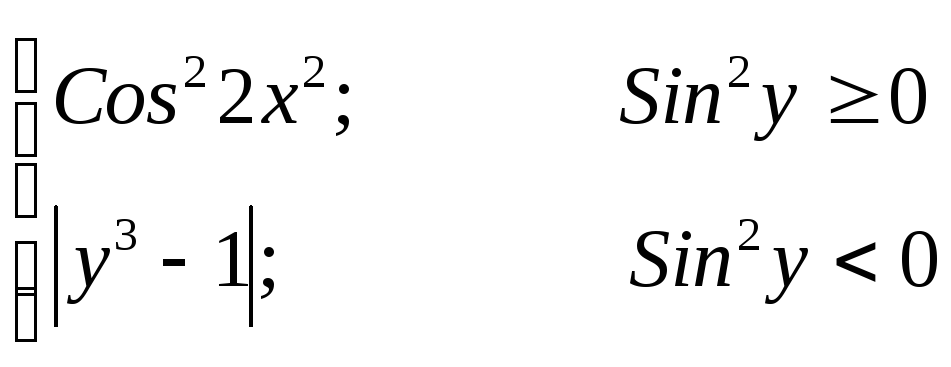
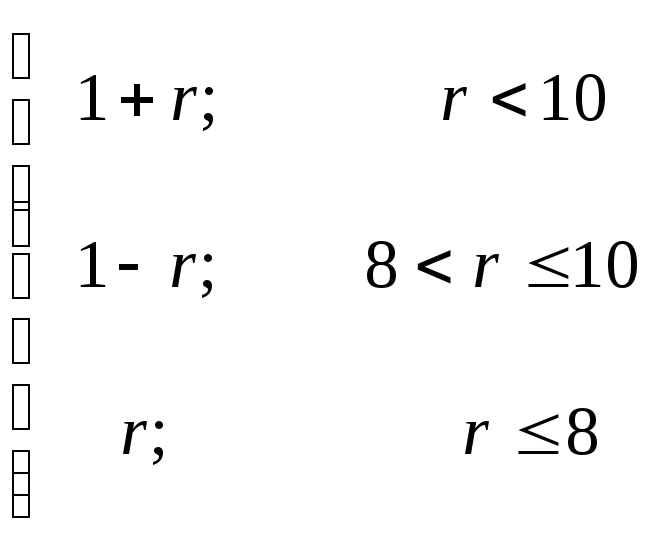
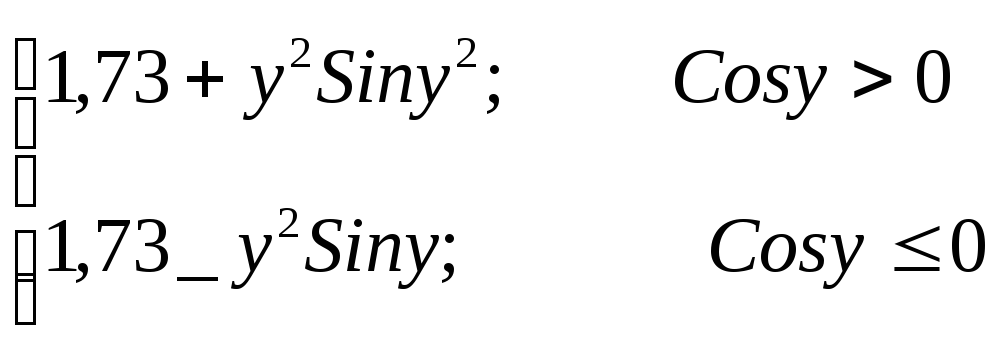
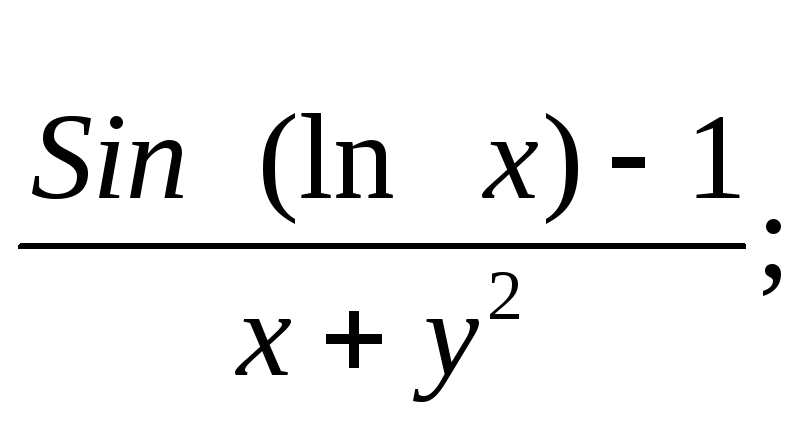 y=
y=