3. Полное исследование функции проводится по следующей схеме:

1) область определения, область значений функции;

2) четность, нечетность функции, периодичность;

3) асимптоты;

4) промежутки монотонности и точки экстремума;

5) промежутки выпуклости и вогнутости графика функции, точки перегиба;

6) точки пересечения графика функции с осями координат;

7) построение графика.

Например:

а) найти асимптоты графика функции .

Решение.

1) Функция не определена в точке . Найдем односторонние пределы функции в этой точке:

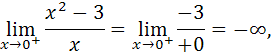
значит, прямая является вертикальной асимптотой.

2) Найдем

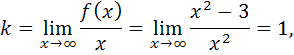
значит, функция имеет наклонную асимптоту , где

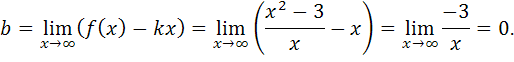
Таким образом, наклонной асимптотой графика функции является прямая .

б) Найти промежутки монотонности и точки экстремума функции

Решение.

1) Найдем производную:

2) определим точки, в которых выполняется необходимое условие экстремума, решив уравнение :

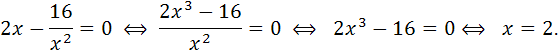
При производная не существует.

Точки и разбивают числовую ось на интервалы ,и .

3) Определим знак производной на полученных промежутках:

Промежуток
Производная

Таким образом, при функция убывает, а при − возрастает. Точка является точкой минимума функции. При этом минимальное значение функции равно

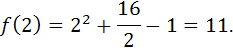
в) Найти промежутки выпуклости (вогнутости) и точки перегиба графика функции

Решение.

1) Найдем производную второго порядка:

2) Найдем точки, в которых выполняется необходимое условие перегиба, решив уравнение

Точка разбивает числовую ось на два интервала: и .

3) Определим знак второй производной на полученных промежутках:

Промежуток		.
Производная второго порядка

Таким образом, при график функции выпуклый вверх, а при − выпуклый вниз (вогнутый).

− точка перегиба, в которой значение функции равно

4. Найти неопределенные интегралы. Результат проверить дифференцированием.

а)

Проверка:

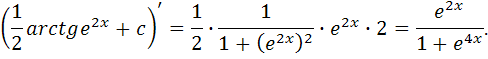
В результате дифференцирования получена подынтегральная функция, значит, интеграл найден верно.

б)

При интегрировании применялась формула интегрирования по частям:

Проверка:

В результате дифференцирования получена подынтегральная функция, значит, интеграл найден верно.

в)

Для отыскания интеграла применяется метод неопределенных коэффициентов, согласно которому

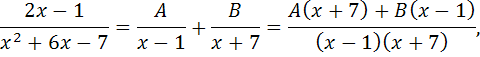
и из полученного равенства следует:

Полагая , получим:

Аналогично, при получаем:

И поэтому,

Проверка:

В результате дифференцирования получена подынтегральная функция, значит, интеграл найден верно.

5. Найти градиент функции в точке , и производную по направлению вектора .

1) Найдем частные производные функции и вычислим их значения в точке .

Учитывая, что получим

2) Найдем направляющие косинусы. Так как , то

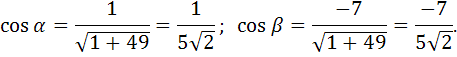
Производная функции по направлению вектора равна

6. Найти общее решение дифференциального уравнения

1) Найдем общее решение однородного уравнения

с помощью характеристического уравнения

Так как характеристическое уравнение имеет два различных действительных корня, то общее решение однородного уравнения равно

2) Частное решение заданного неоднородного уравнения будем искать в виде так как один из корней характеристического уравнения равен −7.

Подставив в уравнение и получим

откуда

Следовательно,

3) Общее решение дифференциального уравнения имеет вид: