Konspekt

Причем I_k – величины алгебраические. Ток считается положительным, если его направление связано с направлением обхода по контуру правилом правого винта. Ток противоположного направления считается отрицательным. Теорема о циркуляции доказывается исходя из закона Био-Савара.

Тот факт, что циркуляция вектора в, вообще говоря, не равна нулю, означает, что поле В не потенциально (в отличие от электростатического). Такое поле называется вихревым или соленоидальным.

Теорема о циркуляции вектора В играет примерно туже роль, что и теорема Гаусса для вектора Е. Циркуляция определяется не всеми токами а только теми которые охватываются контуром. Аналогично ситуации с потоком вектора Е.

Лекция 19

Применение теоремы о циркуляции вектора В. Поле прямого тока. Применение теоремы о циркуляции вектора В. Поле соленоида.

Магнитно поле прямого тока.

Пусть постоянный ток I течет вдоль бесконечно длинного прямого провода, имеющего круглое сечение радиуса а. Необходимо найти индукцию В поля снаружи и внутри провода.

Из симметрии задачи следует, что линии вектора В в данном случае должны иметь вид окружностей с центром на оси провода. Причем модуль вектора В должен быть одинаков во всех точках на расстоянии r от оси провода. Поэтому по теореме о циркуляции вектора В для круглого контура , откуда следует, что вне провода

(r>a).

Решение этого вопроса может быть осуществлено и с использование теоремы Био-Савара, но оно оказывается гораздо более сложным.

Внутри провода из тех же соображений симметрии следует, что линии вектора В являются тоже окружностями. Поэтому выбираем контур виде окружности. По теореме о циркуляции для контура внутри провода , где I_r – ток, охватываемый контуром . Он пропорционален площади охватываемой контуром. Отсюда находим, что внутри провода:

.

Таким образом, получили, что внутри провода магнитное поле растет к периферии линейно с r, а вне поле уменьшается обратно пропорционально r. Если провод имеет вид трубки, то снаружи индукция магнитного поля вдет себя таим же образом, а внутри – магнитное поле отсутствует.

Магнитное поле соленоида.

Пусть ток I течет по проводнику, намотанному по винтовой линии на поверхность цилиндра. Такой, обтекаемый током цилиндр называется соленоидом. Пусть на единицу длины соленоида приходится n витков проводника. Если шаг винтовой линии достаточно мал, то каждый виток соленоида можно приближенно заменить замкнутым витком. Предполагается, что сечение проводника настолько мало, что можно считать, что ток течет по поверхности соленоида.

Опыт показывает на то, что в центральной части катушки магнитное поле практически однородно и значительно сильнее, чем вне катушки. В предельном случае бесконечно длинного соленоида однородное магнитное поле целиком сосредоточено внутри соленоида.

Из соображений симметрии ясно, что линии вектора В внутри соленоида направлены вдоль его оси, причем вектор В составляет с направлением тока правовинтовую систему. Такая конфигурация линий поля подсказывает выбрать контур в виде прямоугольника, две стороны которого параллельны линиям поля, причем одна из них находится вне соленоида. Вторые две стороны оказываются перпендикулярны линиям магнитной индукции. В итоге получаем, что циркуляция по трем из четырех сторон прямоугольника равна нулю. По стороне вне соленоида, так как там нет поля. По сторонам перпендикулярным полю, так как проекция линий поля на них равна нулю. Тогда согласно теореме о циркуляции получаем , где l - длина стороны параллельной линиям магнитной индукции. Окончательно получаем, поле внутри длинного соленоида имеет вид:

Т.е. поле внутри длинного соленоида однородно (за исключением областей, прилегающих к торцам соленоида, но этим при расчетах пренебрегаем). Произведение nI называют числом ампервитков.

Магнитное поле тороида.

Тороид представляет собой провод, навитый на каркас, имеющий форму тора. Предполагается, что катушка по которой течет ток I плотно, то есть виток к витку, намотана на немагнитный тороидальный сердечник.

Из соображений симметрии можно понять, что линии вектора В должны быть окружностями, центры которых расположены на оси тороида. Они направлены так, что глядя вдоль них, мы увидели бы ток в витках, циркулирующим по часовой стрелке. Поэтому ясно, что в качестве контура следует взять одну из таких окружностей.

Если контур расположен внутри тороида, то он охватывает N витков с током (N – число витков в тороидальной катушке). Тогда количество токов охватываемых контуром радиуса r равно NI. Следовательно, по теореме о циркуляции получаем , откуда следует, что внутри тороида

Если выбранный нами круглый контур проходит вне тороида, то токов он не охватывает, поэтому для такого контура . Это значит, что вне тороида магнитное поле отсутствует.

Таким образом, модуль вектора магнитной индукции в тороидальной катушке зависит от радиуса r. Если сердечник катушки тонкий, то есть r₂ – r₁ << r, то магнитное поле внутри катушки практически однородно. Величина n = N / 2πr представляет собой число витков на единицу длины катушки. В этом случае

B = μ₀In.

В это выражение не входит радиус тора, поэтому оно справедливо и в предельном случае r → ∞. Но в пределе каждую часть тороидальной катушки можно рассматривать как длинную прямолинейную катушку(соленоид). Вдали от торцов соленоида модуль магнитной индукции выражается тем же соотношением, что и в случае тороидальной катушки.

При расчете поля внутри тороида предполагалось, что линии тока лежат в плоскостях проходящих через ось тороида. У реального тороида витки не лежат строго в этих плоскостях, поэтому имеется оставляющая вокруг оси тороида. Эта составляющая создает дополнительное поле, аналогичное поля кругового тока.

Магнитное поле плоскости с током.

Рассмотрим безграничную проводящую плоскость, по которой течет равномерно распределенный ток одного направления. Введем понятие линейной плотности тока как вектор i, направленный вдоль линий тока. Модуль этого вектора представляет собой ток, приходящийся на единицу длины, которая играет роль поперечного сечения.

Разбив мысленно плоскость с током на тонкие нити с током, нетрудно видеть, что результирующее поле В будет направлено параллельно плоскости, причем направление с разных сторон плоскости будет различным и определяться по правилу правого винта.

Для определения индукции поля В воспользуемся теоремой о циркуляции вектора В. Зная, как расположены в этом случае линии вектора В, выберем контур в виде прямоугольника. Две стороны, которого параллельны плоскости, а две перпендикулярны. Тогда циркуляция вектора В по перпендикулярным сторонам будет равна нулю, так как так как проекция вектора В на них равна нулю. Следовательно по теореме о циркуляции получаем , где l – длина стороны контура, параллельная плоскости с током. В итоге находим

Из полученной формулы видно, что магнитное поле как с одной стороны плоскости, так и с другой является однородным. Этот результат справедлив и для ограниченной пластины с током, но лишь на расстояниях близких к пластине и удаленных от ее краев.

Результаты, полученные в рассмотренных примерах, можно было бы найти и непосредственно с помощью закона Био-Савара. Однако теорема о циркуляции позволяет получить эти результаты значительно проще и быстрее. Вместе с тем надо понимать, что число задач, легко решаемых с помощью теоремы о циркуляции вектора В, небольшое. Примером может служить задача о нахождении магнитного поля на оси кругового тока. Здесь, казалось бы ток имеет хорошую симметрию, однако распределение магнитного поля в пространстве не позволяет найти простой контур и задачу приходится решать с помощью закона Био-Савара. Прямой расчет дает следующее значение для магнитной индукции на оси кругового тока:

,

где R – радиус витка с током I. z – координата точки на оси витка. Отсюда следует, что в центре витка с током (z=0) и на расстоянии z>>R модуль вектора В равен

Лекция 20

Сила Ампера. Работа поля В при перемещении контура стоком.

Каждый носитель тока испытывает действие магнитной силы. Действие этой силы передается проводнику, по которому движутся заряды. В результате магнитное поле действует с определенной силой на сам проводник с током.

Пусть объемная плотность заряда, являющегося носителем тока равна ρ. Выделим мысленно элемент объема dV проводника. В нем находится заряд – носитель тока, равный ρdV. Тогда сила, действующая на элемент dV проводника, может быть записана в виде:

Так как , то

.

Если ток течет по тонкому проводнику, то так как и получим

,

Где dl – вектор, совпадающий по направлению с током и характеризующий элемент длины тонкого проводника. и выражают закон Ампера. Для того, чтобы найти силу Ампера, действующую на весь проводник с током, необходимо провести интегрирование по линейному или объемному элементам тока.

Пусть в пространстве имеется два параллельных проводника. Первый проводник создает в пространстве магнитное поле, на второй проводник, находящейся в поле первого будет действовать сила Ампера. Аналогично и на первый проводник будет действовать поле второго проводника. В результате между проводниками возникают силы притяжения или отталкивания, обусловленные магнитным взаимодействием токов. Можно убедиться в том, что токи, одинаково направленные, притягиваются, а противоположно направленные – отталкиваются.

Результирующая сила Ампера, которая действует на контур с током в магнитном поле, определяется следующим образом:

,

Где интегрирование проводится по всему данному контуру с током. Если магнитное поле однородно, то вектор В можно вынести из-под интеграла и задача сводится к вычислению векторного интеграла . Этот интеграл представляет собой замкнутую цепочку элементарных векторов dl, поэтому он равен нулю. Значит и F=0, т.е. результирующая сила Ампера равна нулю в однородном магнитном поле.

Если магнитное поле неоднородно, то результирующая сила отлична от нуля и определяется с помощью интегрирования. Рассмотрим достаточно маленький плоский контур с током – элементарный контур. Поведение элементарного контура с током удобно описывать с помощью магнитного момента p_m. По определению

,

Где I – ток, текущий по контуру, S – площадь, ограниченная контуром, n – нормаль к контуру, направление которой связано с направлением тока в контуре правилом правого винта. В магнитном отношении элементарный контур с током вполне характеризуется его магнитным моментом p_m. Подробный расчет по формуле , с учетом малости контура приводи к следующему выражению для силы, действующей на элементарный контур с током в неоднородном магнитном поле:

- производная вектора В по направлению нормали n или по направлению вектора p_m. Из анализа полученной формулы можно сделать следующие выводы:

1. как и ожидали, в однородном магнитном поле F=0, так как;

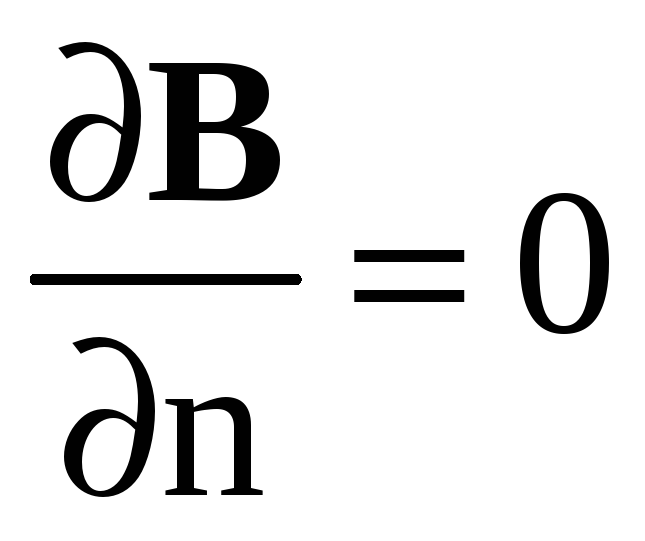2. направление вектора F, вообще говоря, не совпадает с вектором p_m; вектор F

совпадает лишь с направлением элементарного приращения вектора B, взятого в направлении вектора p_m в месте расположения контура.

В частном случае, если вектор магнитной индукции изменяется только в том же направлении, в котором направлен вектор B, можно направить ось x по вектору B. Пусть кроме того величина вектора магнитной индукции возрастает в направлении оси x , т. е.. При этом знак проекции силы, действующей на контур, будет определяется знаком проекции p_mx. Иными словами, если угол между магнитным моментом контура и осью x острый (p_mx>0), то сила направлена в сторону оси, т.е. в сторону возрастания величины индукции. Если угол тупой (p_mx<0), то сила направлена в противоположную сторону. На каждый элемент провода действует сила dF, проекция dF_x которой для всех элементов направлена в одну сторону и складывается в общую силу. Если магнитный момент направлен параллельно магнитной индукции, результирующая сила F направлена в сторону возрастания модуля магнитной индукции. Если же магнитный момент направлен антипараллельно, сила направлена в сторону убывания модуля B.

Найдем момент сил (вращательный момент), действующий на контур с током в однородном магнитном поле. При этом учтем известный из механики факт, что если результирующая сил равна нулю, то момент сил не зависит от выбора точки, относительно которой он вычисляется. Рассмотрим прямоугольный контур со сторонами a b, расположенный в однородном магнитном поле так, что вектор нормали n образует с вектором В угол a , и стороны контура перпендикулярны вектору В.

Обозначим силы Ампера, действующие на стороны контура F₁, F₂, F₃, F₄ . Найдем суммарный момент этих сил относительно центра контура. Линии действия сил F₂,F₄ проходят через точку О, следовательно, моменты этих сил равны нулю. Две другие силы: F₁ и F₃ и радиус-векторы точек их приложения r₁ и r₃ лежат в плоскости, образованной векторами B и n . Каждая из сил F₁, F₃ перпендикулярна вектору В, а радиус-векторы r₁, r₃ перпендикулярны вектору n. Поэтому силы F₁, F₃ образуют с радиус-векторами r₁, r₃ тот же угол a, что и вектор B с нормалью n. Момент этих сил N равен

Слагаемые в этой сумме направлены в одну сторону. По формуле (для силы Ампера) обе силы равны F₁=F₃=IaB, кроме того, r₁=r₃=a/2. Поэтому слагаемые одинаковы по величине и равны

а величина результирующего момента

где S = ab – площадь рамки. Воспользовавшись определением магнитного момента контура, можно записать величину момента сил Ампера, действующих на этот контур:

Векторы p_m, B, N составляют правую тройку векторов, поэтому в общем виде получаем

.

Можно доказать, что данная формула справедлива в однородном магнитном поле для контура произвольной формы. Для момента сил Ампера, существует два положения a = 0 и a = p, в которых этот момент обращается в нуль. В остальных случаях вращающий момент, действующий на контур с током, стремится развернуть контур так, чтобы направление магнитного момента контура совпало с направлением магнитной индукции внешнего поля, т.е. к состоянию a = 0. Поэтому при a = 0 контур оказывается в устойчивом равновесии, а при a = p – в неустойчивом.

Элементарная работа dА, совершаемая силой Ампера dF при перемещении на dr в магнитном поле элемента проводника dl, равна

Здесь, подставив выражение для силы Ампера, вынесли скалярную величину – силу тока I и воспользовались известным свойством смешанного произведения векторов: оно не изменяется при циклической перестановке сомножителей. Векторное произведение перемещения и элемента проводника есть вектор площадки, прочерченной проводником при его перемещении

Скалярное произведение вектора площадки и вектора магнитной индукции – это магнитный поток через площадку dS

поэтому для работы получаем

Если проводник, сила тока I в котором поддерживается постоянной, совершает конечное перемещение из положения 1 в положение 2, то работа сил Ампера при таком перемещении

где Ф – магнитный поток через поверхность, прочерченную проводником при рассматриваемом перемещении.

Если в постоянном магнитном поле перемещается замкнутый контур, то поток, прочерченный всеми элементами контура, равен изменению потока пронизывающего контур. Докажем это.

Предположим есть два последовательных состояния контура С₁ и С₂. Поверхности S₁ и S₂, которые ограничивает контур в положениях С₁ и С₂ и поверхность S_п, прочерченная контуром, составляют замкнутую поверхность. По теореме Остроградского-Гаусса для магнитной индукции суммарный поток через эту замкнутую поверхность равен нулю. Выберем нормали n₁ и n₂ к поверхностям S₁ и S₂ при вычислении потоков Ф₁ и Ф₂ в каждом из положений так, чтобы они были согласованы с направлением тока в контуре по правилу правого винта (из конца вектора нормали ток в контуре виден идущим против часовой стрелки). При этом поток наружу из замкнутой поверхности складывается из потока через S₁ в направлении n₁ (равен Ф₁), потока через S₂ в направлении противоположном n₂ (равен -Ф₂) и потока через прочерченную поверхность S_п (Ф). Таким образом, получаем

откуда Ф=Ф₂-Ф₁. Следовательно, соотношение для замкнутого контура можно записать так

При выводе этой формулы мы рассмотрели простое перемещение контура, но она оказывается справедливой и при более сложных изменениях состояния контура, например, при вращении и при деформации. В приведенном виде она выполняется для движении не только одиночного контура, но и катушки, состоящей из нескольких витков, в частности, для катушки из N одинаковых витков. В последнем случае потокосцепление равно Y = NF_м, где F_м – магнитный поток через один виток.

Лекция 21

Виды поляризации диэлектриков. Поляризованность Р.

Свойства поля вектора Р. Вектор D. Условия на границе двух

диэлектриков для векторов E и D

Вещество, внесенное в электрическое поле, может существенно изменить его. Это связано с тем, что вещество состоит из заряженных частиц. В отсутствие внешнего поля частицы распределяются внутри вещества так, что создаваемое ими электрическое поле в среднем по объемам, включающим большое число атомов или молекул, равно нулю. В диэлектриках нет свободных электрических зарядов. Они состоят из нейтральных атомов или молекул. Заряженные частицы в нейтральном атоме связаны друг с другом и не могут перемещаться под действием электрического поля по всему объему диэлектрика.

При внесении диэлектрика во внешнее электрическое поле Е₀ в нем возникает некоторое перераспределение зарядов, входящих в состав атомов или молекул. В результате такого перераспределения на поверхности и, вообще говоря, и в объеме диэлектрического образца появляются избыточные нескомпенсированные связанные заряды. Все заряженные частицы, образующие макроскопические связанные заряды, по-прежнему входят в состав своих атомов.

Связанные заряды создают электрическое поле Е’ которое внутри диэлектрика направлено противоположно вектору напряженности Е₀ внешнего поля. Этот процесс называется поляризацией диэлектрика. В результате полное электрическое поле Е=Е₀+Е’ внутри диэлектрика оказывается по модулю меньше внешнего поля E₀. Существует несколько механизмов поляризации диэлектриков. Основными из них являются ориентационная и электронная поляризации. Первый механизм работает при поляризации полярных диэлектриков, второй – неполярных.

В случае полярных диэлектриков, состоящих из молекул, у которых центры распределения положительных и отрицательных зарядов не совпадают. Такие молекулы представляют собой микроскопические электрические диполи – нейтральную совокупность двух зарядов, равных по модулю и противоположных по знаку, расположенных на некотором расстоянии друг от друга. Дипольным моментом обладает, например, молекула воды, а также молекулы ряда других диэлектриков. Дипольным моментом диполя называется векторная величина:_. Вектор l направлен от –q к +q

При отсутствии внешнего электрического поля оси молекулярных диполей ориентированы хаотично из-за теплового движения, так что на поверхности диэлектрика и в любом элементе объема электрический заряд в среднем равен нулю. При внесении диэлектрика во внешнее поле Е₀ возникает частичная ориентация молекулярных диполей. В результате на поверхности диэлектрика появляются нескомпенсированные макроскопические связанные заряды, создающие поле Е’ направленное навстречу внешнему полю.

Электронный механизм проявляется при поляризации неполярных диэлектриков, молекулы которых не обладают в отсутствие внешнего поля дипольным моментом. Под действием электрического поля молекулы неполярных диэлектриков деформируются – положительные заряды смещаются в направлении вектора Е₀ а отрицательные – в противоположном направлении. В результате каждая молекула превращается в электрический диполь, ось которого направлена вдоль внешнего поля.

Каждый малый объем dV (малый по сравнению с объемом диэлектрического тела, но большой по сравнению с объемом молекулы, атома или элементарной ячейки кристалла) приобретает дипольный момент

где N – число элементарных диполей (p_i– дипольные моменты молекул) в объеме dV.. Число N пропорционально dV (N = ndV, где n – концентрация молекул). Поэтому векторная величина

{Кл/м²)

называемая поляризованностью (численно равная дипольному моменту единичного объема диэлектрической среды) не зависит от dV. Для диэлектриков зависимость поляризованности от напряженности электрического поля линейна:

Где - безразмерная величина, называемая диэлектрической восприимчивостью вещества. Эта величина не зависит от Е она характеризует свойства самого диэлектрика.

Поле вектора Р обладает следующим свойством: поток вектора Р сквозь произвольную замкнутую поверхность S равен взятому с обратным знаком избыточному связанному заряду диэлектрика в объеме, охватываемом поверхностью S

Это уравнение выражает теорему Гаусса для вектора Р.

Поскольку источниками поля Е являются все электрические заряды – сторонние и связанные, теорему Гаусса для поля Е можно записать так:

Где q и q’ – сторонние и связанные заряды, охватываемы поверхностью S. Появление связанных зарядов q’ усложняет дело, и данная формула оказывается мало применима для нахождения поля Е в диэлектрике. Действительно эта формула выражает свойства неизвестного поля Е, через связанные заряды, которые в свою очередь определяются неизвестным полем Е. Если выразить связанный заряд через поток вектора Р, тогда выражение для потока вектора Е можно преобразовать к следующему виду:

Величину, стоящую под интегралом в скобках, обозначают буквой D. В итоге получили вспомогательный вектор D:

Поток которого сквозь произвольную замкнутую поверхность равен алгебраической сумме сторонних зарядов, охватываемых этой поверхностью:

Это утверждение называют теоремой Гаусса для поля вектора D. Вектор D представляет собой сумму двух совершенно различных величин и Р. Поэтому он действительно вспомогательный вектор, не имеющий какого-либо глубокого физического смысла. Однако во многих случаях он значительно упрощает изучение поля в диэлектрике.