ИИТиАС - II_1 / Лабораторный компьютерный кп (Коновалов, Олесюк)

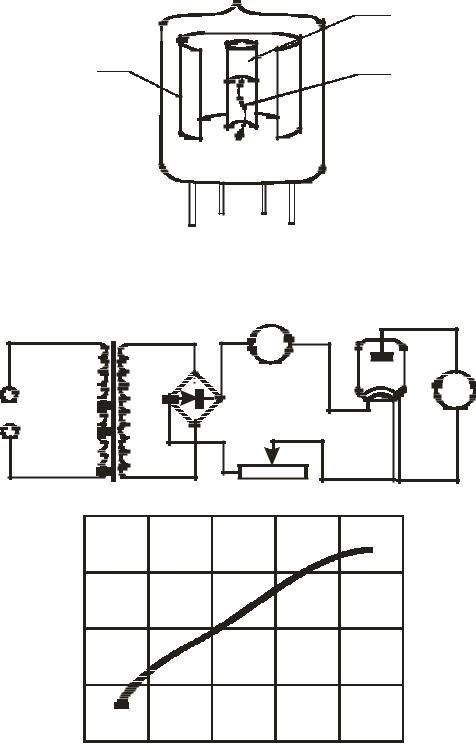
перметром ИП1, с помощью градуировочной кривой (рисунок 4). Для измерения тока IA термоэлектронов, попадающих на анод, служит микроамперметр ИП2, включенный в анодную цепь. Прибор ИП2 также расположен на лицевой панели установки.

1 - катод; 2 - спираль подогрева; 3 – анод

Рисунок 2 – Двухэлектродная электронная лампа

Рисунок 3 – Схема экспериментальной установки

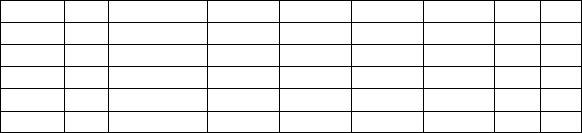
Рисунок 4 – Градуировочная кривая для определения температуры катода

21

ЗАДАНИЕ Измерить зависимость тока термоэлектронов от температуры катода.

Нанести экспериментальные точки на график в координатах ln I и 1/T. Убедиться в наличии линейной зависимости. Определить работу выхода электронов из металла.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1.Включить установку, нажав кнопку «Сеть» на лицевой панели. Выждать время, необходимое для установления стационарного режима, и записать значения тока накала IН и анодного тока IA в таблицу 1.

2.Повторить измерения 7-8 раз, устанавливая каждый раз новое значение тока накала и, выжидая около минуты, пока температура катода стабилизируется.

3.Определить и занести в таблицу значения температуры катода с помощью градуировочной кривой, вычислить величины 1/T.

4.Вычислить значения ln IA и занести их в таблицу.

5.Нанести экспериментальные точки на график в координатах ln IА и 1/T.

6.Определить погрешности измерения экспериментальных точек и нанести их на график.

7.Провести интерполирующую прямую.

8.Определить работу выхода электронов из металла.

Таблица 1 – Расчетные параметры

IH

IA

T

Ln IA

1/T

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Что называется распределением Больцмана?

2.Сколько значений потенциальной энергии частиц реализуется в экспериментальной установке, применяемой в данной работе?

3.Представить распределение Больцмана графически и указать на графике область изменения параметров системы в данной работе.

4.Что общего и в чем различие распределений Больцмана и Максвелла?

5.Какова физическая причина существования работы выхода электронов из металла? Что было бы, если бы работа выхода равнялась нулю или была отрицательной?

К данной работе смотрите список литературы [1-5].

22

Лабораторная работа 4 кп

ИЗУЧЕНИЕ МАГНИТНОГО ПОЛЯ КРУГОВОГО ТОКА

ВВЕДЕНИЕ Целью данной работы является изучение магнитного поля на оси вит-

ка с током и экспериментальная проверка закона Био-Савара-Лапласа.

КРАТКАЯ ТЕОРИЯ Согласно закону Био-Савара-Лапласа каждый элемент проводника с

током Idl создает в точке с радиусом-вектором r магнитное поле с индукцией

где µ0 – магнитная постоянная (4π·10-7 Гн/м).

Из свойства векторного произведения следует, что векторы dB, dl и r образуют правовинтовую систему, т.е. элементарный вектор магнитной индукции всегда перпендикулярен плоскости, в которой лежат векторы dl и r. Используя выражение (1) и принцип суперпозиции, можно рассчитать магнитное поле, создаваемое проводником с током любой формы. Рассчитаем индукцию магнитного поля на оси витка с током (на оси кругового тока) на расстоянии z от центра витка (рисунок 1а).

Рисунок 1 – Конфигурация магнитного поля, создаваемого круговым током

Векторы индукции dB, создаваемые разными элементами тока I·dl, образуют конический веер, как показано на рис.1б. Из соображений симметрии можно заключить: результирующий вектор B направлен вдоль оси кругового контура. В результирующий вектор B вносят вклад только составляющие элементарных векторов B, параллельные оси кругового тока (см. рисунок 1а), равные по модулю

23

dB·sinβ = (R/r)·dβ.

Угол между векторами dl и r всегда прямой, поэтому

Проинтегрировав (2) по всему контуру и заменив r на (R2+z2)1/2 (см. рис.1а), получим

Полученное выражение (3) определяет величину индукции магнитного поля на оси кругового тока. Как следует из (3), магнитная индукция не зависит от знака a. Это значит, что в точках на оси z, симметричных относительно центра витка с током, вектор B имеет одинаковую величину и направление. При а = 0 выражение (3) переходит в выражение для индукции магнитного поля в центре кругового тока

В реальном случае поле создается не одним витком, а катушкой, содержащей некоторое число витков N. Это позволяет получать значительное по величине магнитное поле, пропуская в катушке небольшой ток. Если длина катушки значительно меньше радиуса R ее поперечного сечения, то для приближенного расчета поля катушки можно использовать выражение (3), подставляя вместо тока I величину N·I.

Если катушка питается переменным синусоидальным током, то индукция магнитного поля, создаваемого этой катушкой, также изменяется во времени по закону синуса:

B(t) = Bm·sin(ωt),

где Bm – максимальное (амплитудное) значение магнитной индукции; ω – циклическая частота переменного тока.

МЕТОДИКА ИЗМЕРЕНИЙ Для измерения магнитной индукции можно использовать различные

проявления магнитного поля, например, эффект Холла, явление электромагнитной индукции, действие на магнитную стрелку и др. В данной работе использовано явление электромагнитной индукции. Это явление заключается в том, что если катушку, состоящую из некоторого числа витков N1, пронизывает переменный во времени магнитный поток, то в ней возникает

24

ЭДС индукции, прямо пропорциональная скорости изменения этого потока и числу витков:

где Фn(t) – нормальная составляющая переменного магнитного потока, пронизывающего площадь поперечного сечения катушки

S.

Так как Фn(t) = Bn(t)S, выражение (5) можно представить в виде

где Bn – максимальное значение нормальной составляющей переменной магнитной индукции Bn(t).

1 – катушка с током, создающая магнитное поле; 2 – измерительная катушка; 3 – осциллограф

Рисунок 2 – Схематическое изображение экспериментальной установки

ЭДС индукции в измерительной катушке (рисунок 2) создается изменяющимся интегральным магнитным потоком Фn(t). Значение магнитной индукции Bn в выражении (6) является усредненным по площади сечения измерительной катушки. Это значит, что оно всегда меньше истинного значения магнитной индукции на оси витка с током и тем ближе к нему, чем меньше поперечное сечение измерительной катушки. В данной работе эта площадь на несколько порядков меньше площади витка с током, создающим магнитное поле (см. рисунок 2). Приближенно можно считать величину Bn равной амплитудному значению магнитной индукции Bm, соз-

25

даваемой круговым током на оси z. В выражении (5) множитель перед функцией cosωt представляет собой амплитудное значение ЭДС

Таким образом, измерив ЭДС индукции и используя соотношение (7), можно рассчитать амплитудное значение индукции магнитного поля на оси катушки с током (см. рисунок 2). Измерение ЭДС индукции можно осуществить с помощью измерительного прибора, например, милливольтметра или осциллографа. Окончательное выражение для расчета амплитудного значения магнитной индукции в любой точке на оси z имеет вид

где εm – амплитудное значение ЭДС катушки, измеренное с помощью осциллографа;

S – площадь поперечного сечения измерительной катушки (в данной работе S = 3·10-4 м2);

ω=2πν, где ν – частота переменного напряжения, питающего круговой виток (ν = 50 Гц);

N1 – число витков измерительной катушки.

Для лабораторного макета с номером Nмак число витков измерительной катушки вычисляется по формуле N1 = 3000+20·Nмак. Экспериментальная установка, схематично представленная на рисунке 2, состоит из катушки 1 с током, создающей магнитное поле, измерительной катушки 2 и осциллографа 3. Катушка 1 питается через понижающий трансформатор переменным током. Все устройство смонтировано на лабораторном макете. Измерительная катушка 2 расположена под лицевой панелью макета и может перемещаться вдоль оси катушки 1 с помощью движка.

ЗАДАНИЕ И ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1.Задание. Исследовать экспериментальную зависимость индукции Bm магнитного поля кругового тока на его оси от расстояния z до центра витка.

2.Порядок выполнения работы

а) Подключить лабораторный макет и осциллограф к сети переменного напряжения ~ 220 В.

б) Перемещая измерительную катушку через 1 см, снять зависимость εm от z. Измеренные величины внести в таблицу 1.

в) По формуле (8) рассчитать индукцию магнитного поля Bm для z=0. Оценить погрешность величины Bm при а = 0.

26

г) Построить график зависимости εm=f1(z).

д) Проверить соответствие экспериментальной зависимости εm= f1(z) уравнению (3), используя метод линеаризации. Для этого, учитывая (7), можно представить (3) в виде

Используя экспериментальные данные, построить график зависимости (εm)-2/3=f2(а2). Если точки в этой зависимости укладываются на прямую (в

пределах их погрешностей), то экспериментальная зависимость εm=f1(а) соответствует теоретической, т.е. закону Био-Савара-Лапласа.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Что такое магнитное поле? Каковы его основные характеристики?

2.Какое из проявлений магнитного поля используется в данной работе при измерении магнитной индукции?

3.Почему размеры измерительной катушки (ее поперечное сечение) должны быть значительно меньше размеров витка с током, создающего магнитное поле?

4.Как измерить амплитуду электрического сигнала с помощью осциллографа?

5.По какому закону изменяется индукция магнитного поля на оси кругового тока? Записать этот закон.

6.Как проверить соответствие экспериментально измеренной зависимости εm(а) теоретической, т.е. закону Био-Савара-Лапласа?

7.Какими способами можно построить прямую по экспериментальным точкам?

Кданной работе смотрите список литературы [6-8].

27

Лабораторная работа 5 кп

ИЗУЧЕНИЕ ЗАТУХАЮЩИХ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ

ВВЕДЕНИЕ Целью данной работы является изучение работы колебательного конту-

ра, свободных затухающих электромагнитных колебаний и их характеристик.

КРАТКАЯ ТЕОРИЯ Для возбуждения и поддержания электромагнитных колебаний ис-

пользуют колебательный контур, который представляет собой замкнутую цепь, состоящую из последовательно соединенных конденсатора емкостью С, катушки индуктивности L и омического сопротивления R. Причем омическое сопротивление включает в себя сопротивление соединенных проводов, сопротивление провода катушки индуктивности и сопротивление включенного в контур резистора. Принципиальная схема колебательного контура приведена на рисунке 1.

Рисунок 1 – Колебательный контур

Рассмотрим, как возникают колебания в контуре. В начальный момент с помощью генератора одиночных импульсов конденсатор заряжается до некоторой разности потенциалов U на его обкладках. При этом обкладкам конденсатора сообщен заряд ±q. Энергия электрического поля конденсатора WC = CU2/2. Если теперь генератор отключить, а конденсатор замкнуть на катушку с индуктивностью L, то начнется его разрядка и в катушке возникнет ток. Это возрастающий от нуля ток приводит к возникновению магнитного поля. Следовательно, энергия электрического поля между обкладками конденсатора постепенно переходит в энергию магнитного поля катушки. В момент разрядки конденсатора ток в катушке достигает максимального значения и энергия магнитного поля WL = LI2/2. Когда полностью разрядился конденсатор, то, казалось бы, ток в катушке должен прекратиться. Но уменьшению тока в катушке препятствует явление самоиндукции, поддерживающее ток в прежнем направлении. Этот убывающий ток продолжает переносить заряды от одной обкладки конденсатора к дру-

28

гой в том же направлении и перезаряжает конденсатор. Перезарядка заканчивается, когда ток становится равным нулю. В этот момент энергия магнитного поля катушки переходит в энергию электрического поля конденсатора. В следующий момент начинает разряжаться конденсатор, при этом ток течет в обратном направлении.

Разрядный ток возрастает, пока конденсатор не разрядится полностью, а затем убывает, но вследствие явления самоиндукции снова перезаряжается конденсатор и контур возвращается в исходное состояние. Этим завершается один период колебаний в контуре.

Взаимное превращение энергии электрического и магнитного полей сопровождается потерями энергии на нагревание проводников. И если энергия не пополняется извне, то колебания в контуре затухают - амплитуда тока каждого последующего колебания меньше амплитуды предыдущего колебания. Чем больше омическое сопротивление контура, тем быстрее затухают колебания в нем. Закон затухания колебаний зависит от свойств колебательной системы.

Система называется линейной, если параметры, характеризующие данную систему в рассматриваемом процессе, не изменяются. Линейные системы описываются линейными дифференциальными уравнениями. Электрический контур можно считать линейной системой, если его сопротивление R, электроемкость C и индуктивность L не зависят ни от тока в контуре, ни от напряжения.

Найдем дифференциальное уравнение, описывающее свободные затухающие колебания линейной системы – электрического колебательного контура. Для этого воспользуемся законом Ома и вытекающим из него вторым правилом Кирхгофа, которые справедливы для цепей постоянного и квазипостоянного токов. В данном случае в цепи протекает переменный ток, но, учитывая, что размеры контура l не слишком велики (т.е. l < c/ν, где c - скорость света, с которой распространяются электромагнитные колебания; l - длина контура; ν - частота контура), можно считать, что мгновенное значение тока будет практически одинаково во всех точках контура. Токи, удовлетворяющие такому условию, называются квазистационарными. Тогда согласно второму закону Кирхгофа для контура, в котором протекают квазистационарные токи, можно записать

29