Сапегина К. 11
.pdf
Решение:
Если функция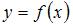 
задана и непрерывна на всей числовой прямой, и 
, 
,
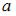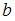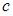– действительные числа, то справедливо следующее свойство определенного интеграла:
,
или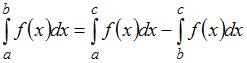 
. Тогда, например, при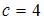 
.
ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Предел функции
Предел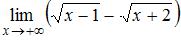 
равен …
0
–3
ЗАДАНИЕ N 23 сообщить об ошибке
Тема: Область определения функции
Область определения функции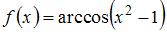 
имеет вид …
Решение:
Данная функция определена, если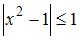 
. Возведем обе части этого неравенства в квадрат и получим 
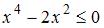, или 
. Решив
последнее неравенство, например, методом интервалов, получаем:
.
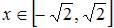ЗАДАНИЕ N 24 сообщить об ошибке
Тема: Основные методы интегрирования
Множество первообразных функции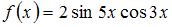 
имеет вид …
Решение:
Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции. Тогда
.
ЗАДАНИЕ N 25 сообщить об ошибке
Тема: Законы распределения вероятностей дискретных случайных величин
Дискретная случайная величина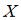 
задана законом распределения вероятностей:
Тогда вероятность |
равна … |
0,8
0,3
0,7
0,4
ЗАДАНИЕ N 26 сообщить об ошибке
Тема: Числовые характеристики случайных величин
Дискретная случайная величина X задана законом распределения вероятностей:
Тогда ее математическое ожидание равно …
4,6
5,0
3,0
4,9
ЗАДАНИЕ N 27 сообщить об ошибке
Тема: Теоремы сложения и умножения вероятностей
Из урны, в которой лежат 3 белых и 7 черных шара, наудачу по одному извлекают два шара без возвращения. Тогда вероятность того, что только один из извлеченных шаров будет белым, равна …
Решение:
Введем обозначения событий: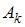 
– k-ый вынутый шар будет белым, A – только один из извлеченных шаров будет белым. Тогда 
, и так как по условию задачи события 
и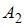 
зависимы, то
.
ЗАДАНИЕ N 28 сообщить об ошибке
Тема: Определение вероятности
Игральная кость бросается два раза. Тогда вероятность того, что сумма выпавших очков – семь, а разность – три, равна …
0
ЗАДАНИЕ N 29 сообщить об ошибке
Тема: Производственные функции
Задана производственная функция 
. Тогда предельный продукт капитала при 
, 
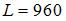равен …
Решение:
Предельный продукт капитала вычисляется по формуле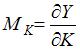 
. Тогда
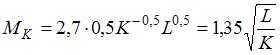. А в точке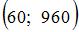 
.
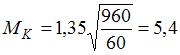ЗАДАНИЕ N 30 сообщить об ошибке
Тема: Сетевое планирование и управление
Матрица коэффициентов прямых затрат линейной статической модели
Леонтьева имеет вид 
, а объемы валовых выпусков
представлены вектором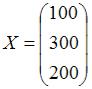 
. Тогда объемы конечного продукта будут представлены вектором …
Решение:
Статическая линейная модель Леонтьева в матричной форме моделируется системой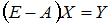 
, где 
– единичная матрица. Следовательно, объемы конечного продукта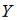 
определяются как 
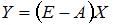, то есть
ЗАДАНИЕ N 31 сообщить об ошибке
Тема: Функции спроса и предложения
Даны функции спроса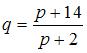 
и предложения 
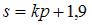, где p – цена товара. Если равновесный объем спроса-предложения равен 
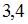, то значение параметра 
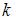равно …
Решение:
Из условия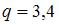 
, или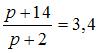 
, определим равновесную цену спросапредложения:
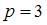. Подставив значения 
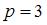и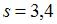 
в уравнение
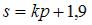, получим искомое значение 
.
ЗАДАНИЕ N 32 сообщить об ошибке
Тема: Функции полезности
Функция полезности потребителя имеет вид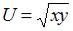 
, а оптимальное потребление: 
, 
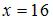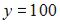. Тогда предельная полезность блага 
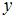равна …
0,8
6,25
0,16
1,25