Макушенко Р. 11

ЗАДАНИЕ N 18 сообщить об ошибке

Тема: Приложения дифференциального исчисления ФОП

Материальная точка движется прямолинейно по закону . Тогда скорость точки в момент времени равна …

Решение:

Скорость движения материальной точки можно определить как производную первого порядка пути 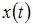по переменной . Тогда

и .

ЗАДАНИЕ N 19 сообщить об ошибке

Тема: Производные первого порядка

Производная функции равна …

Решение:

Предварительно прологарифмируем данную функцию:

, и продифференцируем обе части полученного равенства

.

Тогда .

ЗАДАНИЕ N 20 сообщить об ошибке

Тема: Основные методы интегрирования

Множество первообразных функции имеет вид …

Решение:

Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции методом интегрирования по частям по формуле

. Тогда

.

ЗАДАНИЕ N 21 сообщить об ошибке

Тема: Свойства определенного интеграла

Значение определенного интеграла принадлежит промежутку

…

Решение:

Если функция интегрируема на , и , то

.

Согласно свойств функции наименьшее значение функции на отрезке достигается при и равно

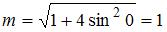, а наибольшее – при 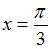и равно

.

Следовательно, ,

или .

ЗАДАНИЕ N 22 сообщить об ошибке

Тема: Предел функции

Предел равен …

4

1

ЗАДАНИЕ N 23 сообщить об ошибке

Тема: Асимптоты графика функции

Наклонная асимптота графика функции задается уравнением вида …

, при , пр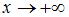и

, при , при

Решение:

Прямая является наклонной асимптотой графика функции при (), если существуют конечные пределы:

, , или, соответственно:

, .

Вычислим эти пределы:

,

.

Следовательно, прямая является наклонной асимптотой графика данной функции при .

,

То есть при наклонной асимптоты у графика данной функции нет.

ЗАДАНИЕ N 24 сообщить об ошибке

Тема: Область определения функции

Область определения функции имеет вид …

Решение:

Область определения данной логарифмической функции определяется как решение системы неравенств:

ЗАДАНИЕ N 25 сообщить об ошибке

Тема: Законы распределения вероятностей дискретных случайных величин

Дискретная случайная величина задана законом распределения вероятностей:

Тогда значения a и b могут быть равны …

ЗАДАНИЕ N 26 сообщить об ошибке

Тема: Определение вероятности

В партии из 12 деталей имеется 5 бракованных. Наудачу отобраны три детали. Тогда вероятность того, что среди отобранных деталей нет бракованных, равна

…

ЗАДАНИЕ N 27 сообщить об ошибке

Тема: Теоремы сложения и умножения вероятностей

Из урны, в которой лежат 3 белых и 7 черных шара, наудачу по одному извлекают два шара без возвращения. Тогда вероятность того, что только один из извлеченных шаров будет белым, равна …

Решение:

Введем обозначения событий: – k-ый вынутый шар будет белым, A – только один из извлеченных шаров будет белым. Тогда , и так как по условию задачи события и зависимы, то

.

ЗАДАНИЕ N 28 сообщить об ошибке

Тема: Числовые характеристики случайных величин

Дискретная случайная величина X задана законом распределения вероятностей:

Тогда ее дисперсия равна …

7,56

3,2

3,36

6,0

Решение:

Дисперсию дискретной случайной величины 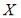можно вычислить по формуле 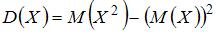. Тогда

.

ЗАДАНИЕ N 29 сообщить об ошибке

Тема: Функции спроса и предложения

Даны функции спроса 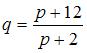и предложения , где p – цена товара. Тогда равновесный объем спроса-предложения равен …

ЗАДАНИЕ N 30 сообщить об ошибке

Тема: Функции полезности

Функция полезности потребителя имеет вид , а бюджетное ограничение . Оптимальный набор благ потребителя: и , 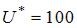. При уменьшении дохода на 1 единицу значение множителя Лагранжа соответствует…

уменьшению функции примерно на ед.

увеличению функции примерно на ед.

увеличению функции примерно в раза уменьшению функции примерно в раза

Решение:

Множитель Лагранжа показывает, насколько примерно уменьшится оптимальное значение функции полезности при уменьшении дохода на 1

единицу. Следовательно, значение соответствует уменьшению функции полезности примерно на единиц.

ЗАДАНИЕ N 31 сообщить об ошибке

Тема: Сетевое планирование и управление

Статическая линейная модель межотраслевого баланса Леонтьева представлена системой уравнений:

Тогда матрица коэффициентов прямых затрат равна …

Решение:

Статическая линейная модель межотраслевого баланса Леонтьева в матричной

форме моделируется системой , где – единичная матрица. Тогда матрица коэффициентов прямых затрат будет равна:

.

ЗАДАНИЕ N 32 сообщить об ошибке

Тема: Производственные функции

Задана производственная функция . Тогда предельный продукт капитала при , равен …

Решение:

Предельный продукт капитала вычисляется по формуле . Тогда

. А в точке

.