
Павловская Я. 11
.pdf
Преподаватель: Базайкина О.Л.
Специальность: 080104.65 - Экономика труда
Группа: ЭЭТ-091 Дисциплина: Математика
Идентификатор студента: Павловская Я.
Логин: 05ps36354
Начало тестирования: 2012-03-11 10:49:47 Завершение тестирования: 2012-03-11 11:40:31 Продолжительность тестирования: 50 мин. Заданий в тесте: 32 Кол-во правильно выполненных заданий: 11
Процент правильно выполненных заданий: 34 %

 ЗАДАНИЕ N 1 сообщить об ошибке
ЗАДАНИЕ N 1 сообщить об ошибке
Тема: Элементы корреляционного анализа
Выборочное уравнение прямой линии регрессии 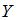 на
на  имеет вид
имеет вид
 . Тогда выборочный коэффициент регрессии равен …
. Тогда выборочный коэффициент регрессии равен …
– 1,5 1,5 4
Решение:
Если выборочное уравнение парной регрессии имеет вид  , то выборочный коэффициент регрессии равен
, то выборочный коэффициент регрессии равен 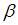 . То есть
. То есть  .
.
 ЗАДАНИЕ N 2 сообщить об ошибке
ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Характеристики вариационного ряда
Медиана вариационного ряда 11, 13, 13, 14, 15,  , 18, 19, 21, 24, 25, 25 равна
, 18, 19, 21, 24, 25, 25 равна
17. Тогда значение варианты  равно …
равно …
16
17
18
15

 ЗАДАНИЕ N 3 сообщить об ошибке
ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Интервальные оценки параметров распределения

Точечная оценка вероятности биномиально распределенного количественного признака равна 0,38. Тогда его интервальная оценка может иметь вид …
Решение:
Интервальная оценка  вероятности
вероятности  биномиально распределенного количественного признака симметрична относительно его точечной оценки, и
биномиально распределенного количественного признака симметрична относительно его точечной оценки, и
 . Таким свойствам удовлетворяет интервал
. Таким свойствам удовлетворяет интервал  .
.

 ЗАДАНИЕ N 4 сообщить об ошибке
ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Проверка статистических гипотез
Соотношением вида  можно определить …
можно определить …


 левостороннюю критическую область
левостороннюю критическую область  правостороннюю критическую область
правостороннюю критическую область
 двустороннюю критическую область
двустороннюю критическую область  область принятия гипотезы
область принятия гипотезы
Решение:
Данное соотношение определяет левостороннюю критическую область, так как левосторонней называют критическую область, определяемую соотношением
 , где
, где  – положительное число, а
– положительное число, а  – уровень значимости.
– уровень значимости.

 ЗАДАНИЕ N 5 сообщить об ошибке
ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Статистическое распределение выборки
Из генеральной совокупности извлечена выборка объема 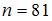 :
:
Тогда значение равно …
34
81
47

33
Решение:
Объем выборки вычисляется по формуле  , где
, где  – частота варианты
– частота варианты 
. Тогда  .
.
 ЗАДАНИЕ N 6 сообщить об ошибке
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Точечные оценки параметров распределения
В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 15; 18; 21; 24. Тогда выборочная дисперсия равна …
11,25
19,5
15
21,25
Решение:
Выборочная дисперсия вычисляется по формуле
 , где
, где  . Вычислив предварительно
. Вычислив предварительно
, получаем
.
 ЗАДАНИЕ N 7 сообщить об ошибке
ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Транспортная задача

Транспортная задача
будет открытой, если …
 ,
, 
 ,
, 
 ,
, 
 ,
, 

 ЗАДАНИЕ N 8 сообщить об ошибке
ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Линейное программирование: графическое задание области допустимых решений
Область допустимых решений OABC задачи линейного программирования имеет вид:
Тогда максимальное значение функции  достигается в точке …
достигается в точке …
B
D
A
C
Решение:
Построим линию уровня  и градиент целевой функции
и градиент целевой функции

 . Тогда целевая функция будет принимать наибольшее значение в точке «выхода» линии уровня из области допустимых решений в направлении градиента.
. Тогда целевая функция будет принимать наибольшее значение в точке «выхода» линии уровня из области допустимых решений в направлении градиента.
Из рисунка видно, что точкой максимума будет точка B как точка «выхода»
линии уровня  из области допустимых решений в направлении градиента.
из области допустимых решений в направлении градиента.
 ЗАДАНИЕ N 9 сообщить об ошибке
ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Сетевое планирование и управление
Сетевой график изображен на рисунке
Тогда, для изменения критического пути, продолжительность работы  можно увеличить на …
можно увеличить на …

 7 дней
7 дней  5 дней
5 дней
 3 дня
3 дня  1 день
1 день

 ЗАДАНИЕ N 10 сообщить об ошибке
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Теория игр: игры с природой
Матрица выигрышей в игре с природой имеет вид
Тогда оптимальной по критерию пессимизма-оптимизма Гурвица относительно выигрышей с показателем пессимизма  будет стратегия …
будет стратегия …

 ЗАДАНИЕ N 11 сообщить об ошибке
ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Производственные функции
Производственная функция  характеризуется неизменной отдачей от масштаба. Тогда параметры
характеризуется неизменной отдачей от масштаба. Тогда параметры  и
и  могут принимать значения …
могут принимать значения …
 ,
, 
 ,
, 
 ,
, 
 ,
, 
Решение:
Производственная функция вида  характеризуется неизменной отдачей от масштаба, если
характеризуется неизменной отдачей от масштаба, если  при
при  . Так как в нашем
. Так как в нашем
случае  , то функция
, то функция  характеризуется неизменной отдачей от масштаба, если
характеризуется неизменной отдачей от масштаба, если  . Этому условию удовлетворяет ответ
. Этому условию удовлетворяет ответ  ,
,  .
.


 ЗАДАНИЕ N 12 сообщить об ошибке
ЗАДАНИЕ N 12 сообщить об ошибке
Тема: Функции полезности
Функция полезности потребителя имеет вид  , а бюджетное ограничение
, а бюджетное ограничение  . Оптимальный набор благ потребителя:
. Оптимальный набор благ потребителя:  и
и
 ,
,  ,
,  . Тогда при увеличении дохода на одну единицу оптимальное значение функции полезности …
. Тогда при увеличении дохода на одну единицу оптимальное значение функции полезности …

 увеличится примерно на 0,5 ед.
увеличится примерно на 0,5 ед.  уменьшится примерно на 0,5 ед.
уменьшится примерно на 0,5 ед.
 увеличится примерно в 2 раза
увеличится примерно в 2 раза  уменьшится примерно в 2 раза
уменьшится примерно в 2 раза
Решение:
Множитель Лагранжа  показывает, насколько примерно увеличится значение функции полезности при увеличении дохода на 1 единицу. Следовательно,
показывает, насколько примерно увеличится значение функции полезности при увеличении дохода на 1 единицу. Следовательно,
значение  соответствует увеличению функции
соответствует увеличению функции  примерно на
примерно на 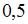 единиц.
единиц.
 ЗАДАНИЕ N 13 сообщить об ошибке
ЗАДАНИЕ N 13 сообщить об ошибке
Тема: Сетевое планирование и управление
В линейной статической модели Леонтьева объемы конечного продукта
представлены вектором  , объемы валовых выпусков – вектором
, объемы валовых выпусков – вектором  . Тогда объемы промежуточной продукции можно представить матрицей …
. Тогда объемы промежуточной продукции можно представить матрицей …

 ЗАДАНИЕ N 14 сообщить об ошибке
ЗАДАНИЕ N 14 сообщить об ошибке
Тема: Функции спроса и предложения
Даны функции спроса по цене  , предложения
, предложения
, и «точка» равновесия |
. Если |
значение параметра уменьшится, то … |
|
равновесная цена спроса-предложения увеличится, а равновесный объем уменьшится
 равновесная цена и равновесный объем спроса-предложения увеличатся
равновесная цена и равновесный объем спроса-предложения увеличатся
равновесная цена спроса-предложения уменьшится, а равновесный объем увеличится
 равновесная цена и равновесный объем спроса-предложения уменьшатся
равновесная цена и равновесный объем спроса-предложения уменьшатся

 ЗАДАНИЕ N 15 сообщить об ошибке
ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Теоремы сложения и умножения вероятностей
Наладчик обслуживает три станка. Вероятность того, что в течение часа потребует его вмешательства первый станок, равна  ; второй –
; второй –  ; третий –
; третий –
 . Тогда вероятность того, что в течение часа потребует вмешательства наладчика только один станок, равна …
. Тогда вероятность того, что в течение часа потребует вмешательства наладчика только один станок, равна …
0,329
0,1
0,45
0,003
Решение:
Введем обозначения событий:  (вмешательства наладчика потребует
(вмешательства наладчика потребует  – ый
– ый
станок),  (вмешательства наладчика потребует только один станок). Тогда
(вмешательства наладчика потребует только один станок). Тогда
.
Учитывая, что , получаем
, получаем


 ЗАДАНИЕ N 16 сообщить об ошибке
ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Определение вероятности
Из урны, в которой находятся 6 белых шаров и 4 черных шара, вынимают одновременно 4 шара. Тогда вероятность того, что среди отобранных 3 шара будут белыми, равна …
Решение:
Для вычисления события  (среди отобранных шаров три шара будут белыми)
(среди отобранных шаров три шара будут белыми)
воспользуемся формулой  , где n – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события A. В нашем случае общее число возможных элементарных исходов равно числу способов, которыми можно
, где n – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события A. В нашем случае общее число возможных элементарных исходов равно числу способов, которыми можно
извлечь четыре шара из десяти имеющихся, то есть  . А общее число благоприятствующих исходов равно числу способов, которыми можно извлечь
. А общее число благоприятствующих исходов равно числу способов, которыми можно извлечь
три белых шара из шести и один черный шар из четырех, то есть  .
.
Следовательно, 

 ЗАДАНИЕ N 17 сообщить об ошибке
ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Законы распределения вероятностей дискретных случайных величин

Дискретная случайная величина  задана законом распределения вероятностей:
задана законом распределения вероятностей:
Тогда ее функция распределения вероятностей имеет вид …
Решение:
По определению  . Тогда а) при
. Тогда а) при  ,
,  , б) при
, б) при  ,
,  ,
,
в) при  ,
,  , г) при
, г) при  ,
,  ,
,
