
Мелихов А. 11
.pdf
Преподаватель: Базайкина О.Л.
Специальность: 080104.65 - Экономика труда
Группа: ЭЭТ-091 Дисциплина: Математика
Идентификатор студента: Мелихов А.
Логин: 05ps36353
Начало тестирования: 2012-03-11 10:48:04 Завершение тестирования: 2012-03-11 11:37:24 Продолжительность тестирования: 49 мин. Заданий в тесте: 32 Кол-во правильно выполненных заданий: 15
Процент правильно выполненных заданий: 46 %

 ЗАДАНИЕ N 1 сообщить об ошибке
ЗАДАНИЕ N 1 сообщить об ошибке
Тема: Функции спроса и предложения
Равновесный объем спроса-предложения равен 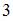 , а равновесная цена спроса-
, а равновесная цена спроса-
предложения равна 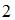 . Тогда функции спроса
. Тогда функции спроса 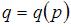 и предложения
и предложения 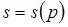 могут иметь вид …
могут иметь вид …
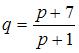 ,
, 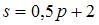
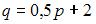 ,
, 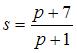
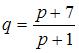 ,
, 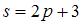
, 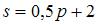
Решение:
В качестве функции спроса 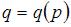 можно взять убывающую функцию, которая проходит через точку с координатами
можно взять убывающую функцию, которая проходит через точку с координатами 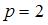 ,
, 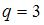 , а в качестве функции предложения
, а в качестве функции предложения 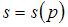 можно взять возрастающую функцию, которая проходит через точку с таким же координатами
можно взять возрастающую функцию, которая проходит через точку с таким же координатами 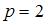 ,
, 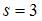 . Этим условиям
. Этим условиям
удовлетворяет, например, пара функций 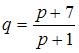 и
и 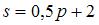 .
.

 ЗАДАНИЕ N 2 сообщить об ошибке
ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Функции полезности
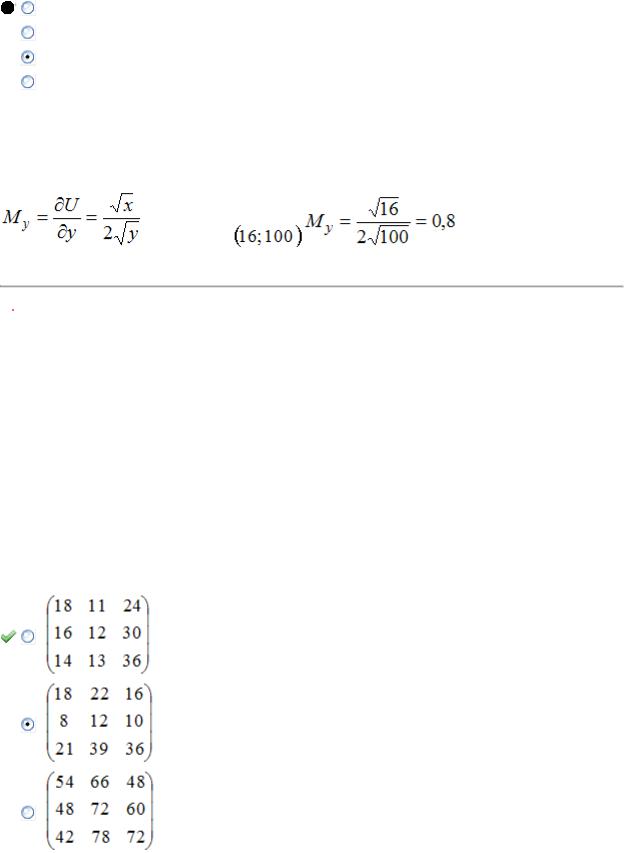
Функция полезности потребителя имеет вид 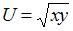 , а оптимальное потребление:
, а оптимальное потребление: 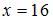 ,
, 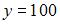 . Тогда предельная полезность блага
. Тогда предельная полезность блага 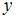 равна …
равна …
0,8
6,25
0,16
1,25
Решение:
Предельная полезность блага 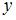 вычисляется по формуле
вычисляется по формуле 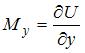 . Тогда
. Тогда
. А в точке |
. |

 ЗАДАНИЕ N 3 сообщить об ошибке
ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Сетевое планирование и управление
Матрица коэффициентов прямых затрат линейной статической модели
Леонтьева имеет вид 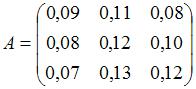 , а объемы валовых выпусков
, а объемы валовых выпусков
представлены вектором 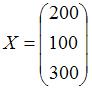 . Тогда объемы промежуточной продукции будут представлены матрицей …
. Тогда объемы промежуточной продукции будут представлены матрицей …
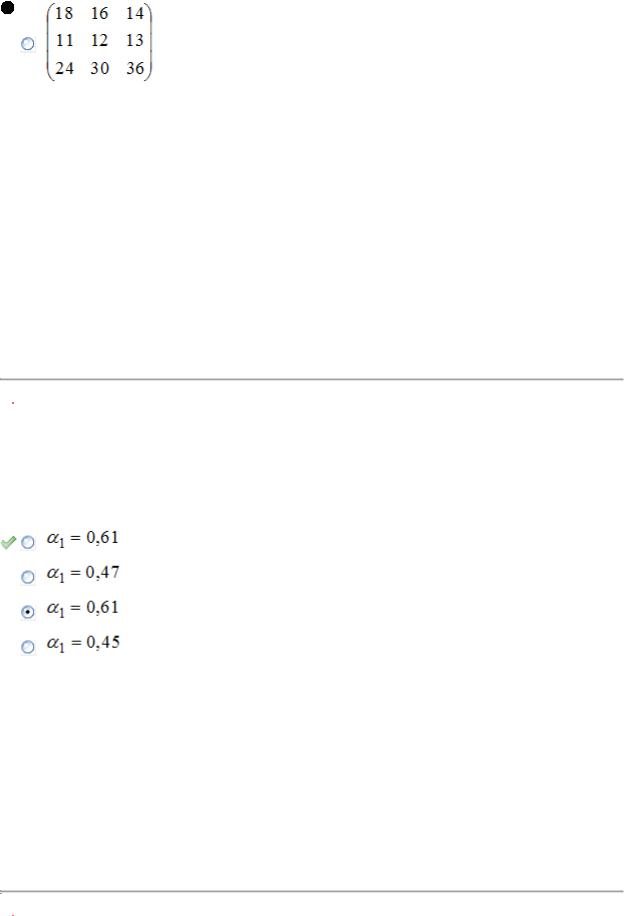
Решение:
Коэффициенты прямых затрат 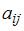 вычисляются по формуле
вычисляются по формуле 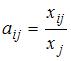 , где
, где 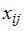 – объем промежуточной продукции
– объем промежуточной продукции 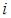 -ой отрасли, который используется в
-ой отрасли, который используется в 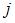 -ой
-ой
отрасли, 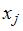 – объем валового выпуска в
– объем валового выпуска в 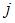 -ой отрасли. Тогда
-ой отрасли. Тогда 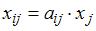 , то
, то
есть 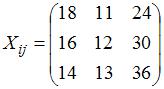 .
.

 ЗАДАНИЕ N 4 сообщить об ошибке
ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Производственные функции
Производственная функция 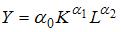 характеризуется возрастающей отдачей от масштаба. Тогда параметры
характеризуется возрастающей отдачей от масштаба. Тогда параметры 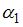 и
и 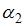 могут принимать значения …
могут принимать значения …
, 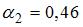 ,
, 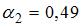 ,
, 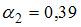 ,
, 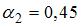
Решение:
Производственная функция вида 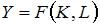 характеризуется возрастающей отдачей от масштаба, если
характеризуется возрастающей отдачей от масштаба, если 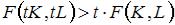 при
при 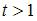 . Так как в нашем
. Так как в нашем
случае 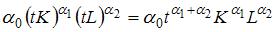 , то функция
, то функция 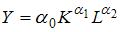 характеризуется возрастающей отдачей от масштаба, если
характеризуется возрастающей отдачей от масштаба, если 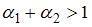 . Этому условию удовлетворяет ответ
. Этому условию удовлетворяет ответ 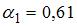 ,
, 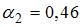 .
.

 ЗАДАНИЕ N 5 сообщить об ошибке
ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Числовые характеристики случайных величин
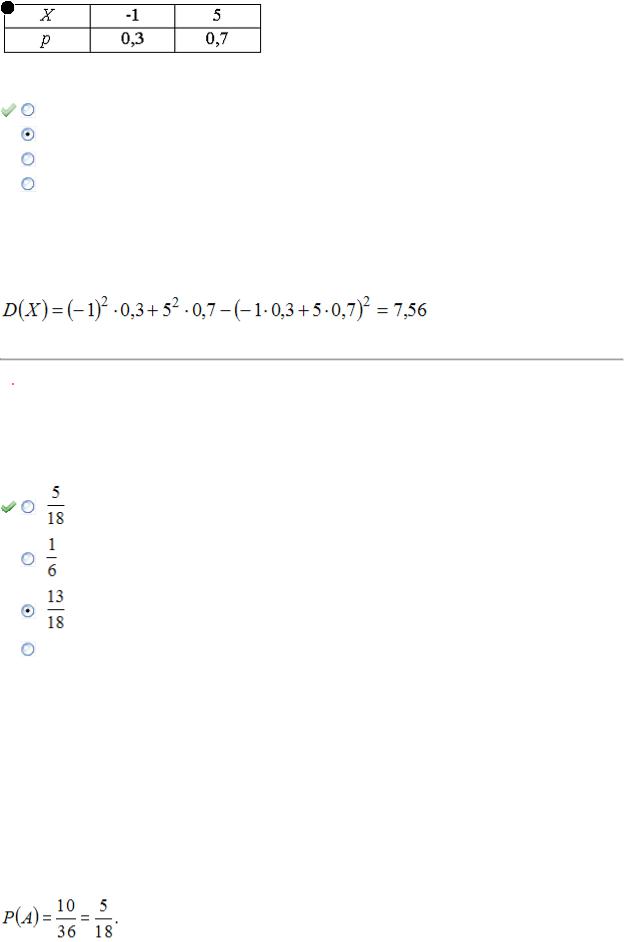
Дискретная случайная величина X задана законом распределения вероятностей:
Тогда ее дисперсия равна …
7,56
3,2
3,36
6,0
Решение:
Дисперсию дискретной случайной величины 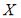 можно вычислить по формуле
можно вычислить по формуле 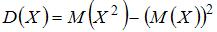 . Тогда
. Тогда
.

 ЗАДАНИЕ N 6 сообщить об ошибке
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Определение вероятности
Игральная кость бросается два раза. Тогда вероятность того, что сумма выпавших очков не меньше девяти, равна …
0
Решение:
Для вычисления события A (сумма выпавших очков будет не меньше девяти)
воспользуемся формулой 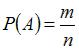 , где n – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события A. В нашем случае возможны
, где n – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события A. В нашем случае возможны
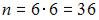 элементарных исходов испытания, из которых благоприятствующими являются исходы вида
элементарных исходов испытания, из которых благоприятствующими являются исходы вида 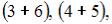
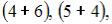
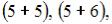
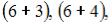
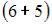 и
и 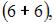 то есть
то есть 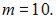 Следовательно,
Следовательно,

 ЗАДАНИЕ N 7 сообщить об ошибке
ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Законы распределения вероятностей дискретных случайных величин
Для дискретной случайной величины 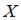 :
:
функция распределения вероятностей имеет вид:
Тогда значение параметра может быть равно …
0,655
1
0,25
0,45
 ЗАДАНИЕ N 8 сообщить об ошибке
ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Теоремы сложения и умножения вероятностей
В электрическую цепь параллельно включены три элемента, работающие независимо друг от друга. Вероятности отказов элементов равны соответственно 0,05, 0,1, 0,20. Тогда вероятность того, что тока в цепи не будет, равна …
0,001
0,35
0,999
0,01

 ЗАДАНИЕ N 9 сообщить об ошибке
ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Дифференциальное исчисление ФНП
Частная производная второго порядка 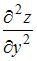 функции
функции 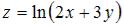 имеет вид
имеет вид
…

Решение:
При вычислении частной производной функции 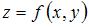 по одной из переменных другую переменную рассматриваем как постоянную величину. Тогда
по одной из переменных другую переменную рассматриваем как постоянную величину. Тогда
.
 ЗАДАНИЕ N 10 сообщить об ошибке
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Свойства определенного интеграла
Среднее значение функции 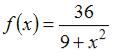 на отрезке
на отрезке 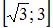 равно …
равно …

 ЗАДАНИЕ N 11 сообщить об ошибке
ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Предел функции
Предел 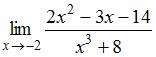 равен …
равен …

Решение:
Разложим числитель и знаменатель на линейные множители как 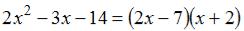 и
и 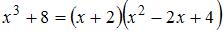 .
.
.
 ЗАДАНИЕ N 12 сообщить об ошибке
ЗАДАНИЕ N 12 сообщить об ошибке
Тема: Приложения дифференциального исчисления ФОП
Материальная точка движется прямолинейно по закону 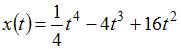 . Тогда скорость точки в момент времени
. Тогда скорость точки в момент времени 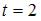 равна …
равна …

 ЗАДАНИЕ N 13 сообщить об ошибке
ЗАДАНИЕ N 13 сообщить об ошибке
Тема: Основные методы интегрирования
Множество первообразных функции 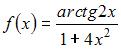 имеет вид …
имеет вид …

Решение:
Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции. Тогда
Произведем замену 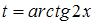 ,
, 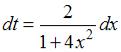 ,
, 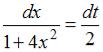 :
:
.

 ЗАДАНИЕ N 14 сообщить об ошибке
ЗАДАНИЕ N 14 сообщить об ошибке
Тема: Область определения функции
Область определения функции 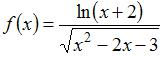 имеет вид …
имеет вид …
Решение:
Данная функция определена, если определен 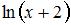 , то есть
, то есть 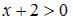 , и подкоренное выражение в знаменателе положительно, то есть
, и подкоренное выражение в знаменателе положительно, то есть 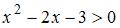 . Решив неравенство
. Решив неравенство 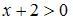 , получаем
, получаем 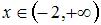 . Для решения неравенства
. Для решения неравенства
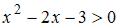 найдем предварительно корни уравнения
найдем предварительно корни уравнения 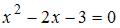 , а именно
, а именно 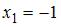 и
и 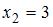 . Тогда методом интервалов можем получить, что
. Тогда методом интервалов можем получить, что
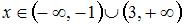 . Следовательно, область определения данной функции будет иметь вид
. Следовательно, область определения данной функции будет иметь вид 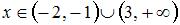 .
.


 ЗАДАНИЕ N 15 сообщить об ошибке
ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Асимптоты графика функции
Горизонтальная асимптота графика функции 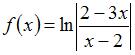 задается уравнением вида …
задается уравнением вида …
Решение:
Прямая 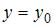 является горизонтальной асимптотой графика функции
является горизонтальной асимптотой графика функции 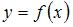
при 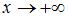 (
(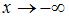 ), если существует
), если существует 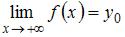 (
(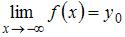 ). Вычислив предел
). Вычислив предел
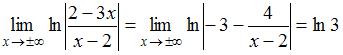 ,
,
получаем уравнение горизонтальной асимптоты 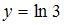 , или
, или 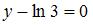 .
.

 ЗАДАНИЕ N 16 сообщить об ошибке
ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Производные первого порядка
Производная функции 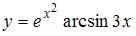 равна …
равна …

Решение:

 ЗАДАНИЕ N 17 сообщить об ошибке
ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Линейные операции над матрицами
Даны матрицы 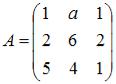 и
и 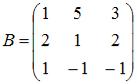 . Если матрица
. Если матрица 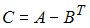 является вырожденной, то значение a равно …
является вырожденной, то значение a равно …
2
0
– 2 5
Решение:
При сложении или вычитании матриц одинаковой размерности соответствующие элементы матриц складываются или вычитаются друг из друга, при транспонировании матрицы соответствующие столбцы матрицы меняются местами со строками с сохранением порядка элементов.
Тогда 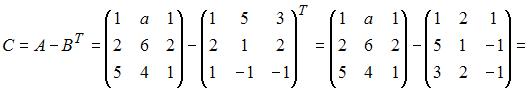
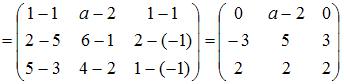 .
.
Так как определитель вырожденной матрицы равен нулю, то вычислим:
Тогда |
и, следовательно |
. |
|
|
|
