
3
.pdf
Решение:
Выборочная дисперсия вычисляется по формуле
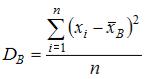 , где
, где  . Вычислив предварительно
. Вычислив предварительно
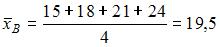 , получаем
, получаем
.

 ЗАДАНИЕ N 24 сообщить об ошибке
ЗАДАНИЕ N 24 сообщить об ошибке
Тема: Интервальные оценки параметров распределения
Дан доверительный интервал  для оценки математического ожидания нормально распределенного количественного признака. Тогда при уменьшении объема выборки этот доверительный интервал может принять вид
для оценки математического ожидания нормально распределенного количественного признака. Тогда при уменьшении объема выборки этот доверительный интервал может принять вид
…
Решение:
Доверительный интервал для оценки математического ожидания нормально распределенного количественного признака можно представить в виде
симметричного интервала  , где точечная оценка
, где точечная оценка


Тогда относительная частота варианты  в выборке равна …
в выборке равна …
0,05
0,06
0,25
0,20
Решение:
Относительная частота  вычисляется по формуле
вычисляется по формуле  , где
, где  – частота варианты
– частота варианты  , а
, а 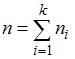 – объем выборки. Вычислим предварительно частоту варианты
– объем выборки. Вычислим предварительно частоту варианты  как
как  . Тогда
. Тогда  .
.

 ЗАДАНИЕ N 27 сообщить об ошибке
ЗАДАНИЕ N 27 сообщить об ошибке
Тема: Элементы корреляционного анализа
Выборочное уравнение прямой линии регрессии  на
на  имеет вид
имеет вид  , а выборочные средние квадратические отклонения равны:
, а выборочные средние квадратические отклонения равны:
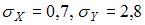 . Тогда выборочный коэффициент корреляции
. Тогда выборочный коэффициент корреляции  равен …
равен …
 ЗАДАНИЕ N 28 сообщить об ошибке
ЗАДАНИЕ N 28 сообщить об ошибке
Тема: Проверка статистических гипотез
Основная гипотеза имеет вид  . Тогда конкурирующей может являться гипотеза …
. Тогда конкурирующей может являться гипотеза …


 ЗАДАНИЕ N 29 сообщить об ошибке
ЗАДАНИЕ N 29 сообщить об ошибке
Тема: Сетевое планирование и управление
В линейной статической модели Леонтьева объемы конечного продукта
представлены вектором  , объемы валовых выпусков – вектором
, объемы валовых выпусков – вектором  . Тогда объемы промежуточной продукции можно представить матрицей …
. Тогда объемы промежуточной продукции можно представить матрицей …
Решение:
В модели Леонтьева валовой выпуск  , конечный продукт
, конечный продукт  и промежуточное потребление
и промежуточное потребление  связаны системой уравнений:
связаны системой уравнений:

Тогда объемы промежуточной продукции можно представить матрицей:
 .
.
 ЗАДАНИЕ N 30 сообщить об ошибке
ЗАДАНИЕ N 30 сообщить об ошибке
Тема: Функции спроса и предложения
Даны функции спроса  и предложения
и предложения  , где p – цена товара. Если равновесный объем спроса-предложения равен
, где p – цена товара. Если равновесный объем спроса-предложения равен  , то значение параметра
, то значение параметра 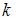 равно …
равно …

 ЗАДАНИЕ N 31 сообщить об ошибке
ЗАДАНИЕ N 31 сообщить об ошибке
Тема: Функции полезности

Функция полезности потребителя имеет вид  , а бюджетное ограничение
, а бюджетное ограничение 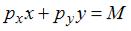 . Оптимальный набор благ потребителя:
. Оптимальный набор благ потребителя:  и
и
 ,
,  ,
,  . Тогда при увеличении дохода на одну единицу оптимальное значение функции полезности …
. Тогда при увеличении дохода на одну единицу оптимальное значение функции полезности …
увеличится примерно на 0,5 ед.
уменьшится примерно на 0,5 ед.
увеличится примерно в 2 раза
уменьшится примерно в 2 раза
Решение:
Множитель Лагранжа  показывает, насколько примерно увеличится значение функции полезности при увеличении дохода на 1 единицу. Следовательно,
показывает, насколько примерно увеличится значение функции полезности при увеличении дохода на 1 единицу. Следовательно,
значение  соответствует увеличению функции
соответствует увеличению функции  примерно на
примерно на  единиц.
единиц.

 ЗАДАНИЕ N 32 сообщить об ошибке
ЗАДАНИЕ N 32 сообщить об ошибке
Тема: Производственные функции
Неоклассическая производственная функция вида  не обладает свойством …
не обладает свойством …

Решение:
Неоклассическая производственная функция вида  обладает
обладает
свойством  , так как с ростом ресурсов выпуск растет;
, так как с ростом ресурсов выпуск растет;
обладает свойством  , так как при отсутствии одного из ресурсов производство невозможно;
, так как при отсутствии одного из ресурсов производство невозможно;
обладает свойством  , так как при неограниченном увеличении одного из ресурсов выпуск неограниченно возрастает.
, так как при неограниченном увеличении одного из ресурсов выпуск неограниченно возрастает.
И неоклассическая производственная функция вида  не обладает свойством
не обладает свойством 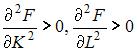 , так как с увеличением ресурсов скорость роста выпуска замедляется, то есть
, так как с увеличением ресурсов скорость роста выпуска замедляется, то есть 

 , а точность оценки
, а точность оценки  . В случае
. В случае будет больше 2,13.
будет больше 2,13.

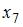 , 12, 13, 15, 16, 18 равна 10. Тогда значение варианты
, 12, 13, 15, 16, 18 равна 10. Тогда значение варианты  равно …
равно … , то медиана равна их средней арифметической, то есть
, то медиана равна их средней арифметической, то есть  . Тогда
. Тогда  .
.

 , полигон частот которой имеет вид:
, полигон частот которой имеет вид: