3

Решение:

Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции. Тогда

.

ЗАДАНИЕ N 22 сообщить об ошибке

Тема: Область определения функции

Область определения функции имеет вид …

ЗАДАНИЕ N 23 сообщить об ошибке

Тема: Производные первого порядка

Производная функции равна …

Решение:

ЗАДАНИЕ N 24 сообщить об ошибке

Тема: Предел функции

Предел равен …

1

ЗАДАНИЕ N 25 сообщить об ошибке

Тема: Дифференциальное исчисление ФНП

Частная производная функции имеет вид …

ЗАДАНИЕ N 26 сообщить об ошибке

Тема: Асимптоты графика функции

Вертикальная асимптота графика функции задается уравнением вида …

Решение:

Прямая является вертикальной асимптотой графика функции , если эта функция определена в некоторой окрестности точки и

, или . Вертикальные асимптоты обычно сопутствуют точкам разрыва второго рода. Определим точки разрыва данной

функции. Это точки, в которых , или 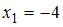, . Однако точка не принадлежит области определения функции , имеющей вид .

Вычислим односторонние пределы функции в точке :

и . Следовательно, прямая будет вертикальной асимптотой.

ЗАДАНИЕ N 27 сообщить об ошибке

Тема: Определение линейного пространства

Среди представленных множеств линейное пространство не образует …

множество всех матриц размерностью m n, содержащих только положительные числа

множество всех векторов, принадлежащих пространству множество всех матриц размерностью m n

множество всех векторов, принадлежащих пространству

Решение:

Множество образует линейное пространство, если для любых 2-х его

элементов определены операции сложения и умножения на действительное число ; со свойствами:

1.

2.

3.

4.

5.

6.

При проверке аксиом получим, что множество всех матриц размерностью m n, содержащих только положительные числа, не образуют линейного пространства, т.к. умножение на отрицательное число получаем матрицу с отрицательными числами и не выполняется шестая аксиома.

ЗАДАНИЕ N 28 сообщить об ошибке

Тема: Вычисление определителей

Определитель равен …

45

135

– 45

– 135

Решение:

Определитель четвертого порядка можно вычислить, например, разложением по

элементам первого столбца:

ЗАДАНИЕ N 29 сообщить об ошибке

Тема: Линейные операции над матрицами

Даны матрицы и . Если матрица является вырожденной, то значение a равно …

2

0

– 2 5

Решение:

При сложении или вычитании матриц одинаковой размерности соответствующие элементы матриц складываются или вычитаются друг из друга, при транспонировании матрицы соответствующие столбцы матрицы меняются местами со строками с сохранением порядка элементов.

Тогда

.

Так как определитель вырожденной матрицы равен нулю, то вычислим:

ЗАДАНИЕ N 30 сообщить об ошибке

Тема: Обратная матрица

Для матрицы существует обратная, если она равна …

Решение:

Всякая невырожденная квадратная матрица имеет обратную матрицу, то есть матрица имеет обратную, если определитель матрицы не равен нулю, тогда

ЗАДАНИЕ N 31 сообщить об ошибке

Тема: Системы линейных уравнений

Система не имеет решений, если равно …

– 2 2 1 0

Решение:

Система не имеет решений, если определитель системы равен нулю и хотя бы один из вспомогательных определителей не равен нулю.

Тогда А, например,

ЗАДАНИЕ N 32 сообщить об ошибке

Тема: Ранг матрицы

Ранг матрицы равен …

3

1

2

4

Решение:

Рангом матрицы называется наибольший из порядков ее миноров, не равных нулю. Так как существуют ненулевые миноры третьего порядка, например:

, то ранг матрицы равен трем.

Преподаватель: Базайкина О.Л.

Специальность: 080104.65 - Экономика труда

Группа: ЭЭТ-091 Дисциплина: Математика

Идентификатор студента: Сапегина К.

Логин: 05ps36355

Начало тестирования: 2012-03-11 10:48:39 Завершение тестирования: 2012-03-11 11:46:55 Продолжительность тестирования: 58 мин. Заданий в тесте: 32 Кол-во правильно выполненных заданий: 21

Процент правильно выполненных заданий: 65 %

ЗАДАНИЕ N 1 сообщить об ошибке

Тема: Линейные операции над матрицами

Дана матрица . Если , где – единичная матрица того же размера, что и матрица 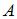, то матрица равна …

Решение:

Матрица находится следующим образом:

.

ЗАДАНИЕ N 2 сообщить об ошибке

Тема: Определение линейного пространства

Среди представленных множеств линейное пространство образует …

множество всех комплексных чисел множество всех натуральных чисел

множество всех положительных иррациональных чисел множество всех отрицательных рациональных чисел

Решение:

Множество образует линейное пространство, если для любых 2-х его

элементов определены операции сложения и умножения на действительное число ; со свойствами:

1.

2.

3.

4.

5.

6.

При проверке аксиом получим: для множества натуральных чисел, множества всех положительных иррациональных чисел и множества всех отрицательных рациональных чисел не выполняется шестая аксиома.

ЗАДАНИЕ N 3 сообщить об ошибке

Тема: Системы линейных уравнений

Единственное решение имеет однородная система линейных уравнений …