3

ЗАДАНИЕ N 13 сообщить об ошибке

Тема: Свойства определенного интеграла

Для определенного интеграла справедливо неравенство …

Решение:

Если функци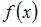и и интегрируемы на , и , то

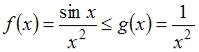. В нашем случае . Тогда

.

ЗАДАНИЕ N 14 сообщить об ошибке

Тема: Область определения функции

Область определения функции имеет вид …

ЗАДАНИЕ N 15 сообщить об ошибке

Тема: Производные первого порядка

Функция задана в параметрическом виде Тогда производная первого порядка функции по переменной имеет вид …

Решение:

.

ЗАДАНИЕ N 16 сообщить об ошибке

Тема: Основные методы интегрирования

Множество первообразных функции имеет вид …

ЗАДАНИЕ N 17 сообщить об ошибке

Тема: Приложения дифференциального исчисления ФОП

К графику функции в его точке с абсциссой проведена касательная. Тогда площадь треугольника, образованного касательной и отрезками, отсекаемыми ею на осях координат, равна …

Решение:

Уравнение касательной к графику функции в его точке с абсциссой имеет вид . Вычислим последовательно

, и .

Тогда уравнение касательной примет вид

.

Эта прямая пересекает оси координат в точках и , то есть отсекает на

Решение:

Статическая линейная модель межотраслевого баланса Леонтьева в матричной

форме моделируется системой , где – единичная матрица. Тогда матрица коэффициентов прямых затрат будет равна:

.

ЗАДАНИЕ N 20 сообщить об ошибке

Тема: Функции полезности

Функция полезности потребителя имеет вид , а бюджетное ограничение . Оптимальный набор благ потребителя: и

, , . Тогда при увеличении дохода на одну единицу оптимальное значение функции полезности …

увеличится примерно на 0,5 ед. уменьшится примерно на 0,5 ед.

увеличится примерно в 2 раза уменьшится примерно в 2 раза

Решение:

Множитель Лагранжа показывает, насколько примерно увеличится значение

функции полезности при увеличении дохода на 1 единицу. Следовательно,

значение соответствует увеличению функции примерно на единиц.

ЗАДАНИЕ N 21 сообщить об ошибке

Тема: Функции спроса и предложения

Даны функции спроса и предложения , где p – цена товара. Если равновесный объем спроса-предложения равен , то значение параметра равно …

ЗАДАНИЕ N 22 сообщить об ошибке

Тема: Производственные функции

Производственная функция с постоянной эластичностью замены (CES) может иметь вид …

ЗАДАНИЕ N 23 сообщить об ошибке

Тема: Сетевое планирование и управление

Для сетевого графика, изображенного на рисунке,

критический путь имеет вид …

ЗАДАНИЕ N 24 сообщить об ошибке

Тема: Теория игр: игры с природой

Матрица рисков в игре с природой имеет вид:

Тогда оптимальной по критерию Байеса относительно рисков будет стратегия

…

Решение:

Вычислим средние риски игрока: , ,

,

оптимальное распределение поставок …

имеет задача B имеет задача A

имеет и задача A и задача B не имеет ни одна из задач

Решение:

В оптимальном распределении сумма потенциалов для свободных клеток должна быть меньше или равна тарифу: 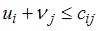. Для задачи A, например,

. То есть, решение неоптимальное. Для задачи B:

.

.

.

. То есть, решение оптимальное. Следовательно, оптимальное распределение имеет задача В.

ЗАДАНИЕ N 27 сообщить об ошибке

Тема: Статистическое распределение выборки

Статистическое распределение выборки имеет вид

Тогда объем выборки равен …

67

40

5

107

ЗАДАНИЕ N 28 сообщить об ошибке

Тема: Проверка статистических гипотез

Для проверки нулевой гипотезы при заданном уровне

значимости выдвинута конкурирующая гипотеза . Тогда область принятия гипотезы может иметь вид …

ЗАДАНИЕ N 29 сообщить об ошибке

Тема: Точечные оценки параметров распределения

Проведено четыре измерения (без систематических ошибок) некоторой

случайной величины (в мм): 8, 9, , 12. Если несмещенная оценка математического ожидания равна 10, то выборочная дисперсия будет равна …

2,5

2,0

0

1,5

Решение:

Вычислим предварительно значение . Так как несмещенная оценка

математического ожидания вычисляется по формуле: , то

. Следовательно, .

Для вычисления выборочной дисперсии применим формулу .

Тогда .