
3
.pdf
 ЗАДАНИЕ N 27 сообщить об ошибке
ЗАДАНИЕ N 27 сообщить об ошибке
Тема: Вычисление определителей
Определитель  равен …
равен …


 ЗАДАНИЕ N 28 сообщить об ошибке
ЗАДАНИЕ N 28 сообщить об ошибке
Тема: Ранг матрицы
Ранг матрицы  равен двум, если значение
равен двум, если значение  не равно …
не равно …
– 1
0
– 2
1
Решение:
Рангом матрицы называется наибольший из порядков ее миноров, не равных нулю. Следовательно, если минор второго порядка не равен нулю, то ранг будет
равен двум. Вычислим  . То есть
. То есть  .
.

 ЗАДАНИЕ N 29 сообщить об ошибке
ЗАДАНИЕ N 29 сообщить об ошибке
Тема: Системы линейных уравнений


для любого  может существовать несколько противоположных элементов
может существовать несколько противоположных элементов 
 для любого
для любого 
 для любого
для любого 
нейтральный элемент  является единственным
является единственным
Решение:
Линейное пространство обладает свойствами:
1. Нейтральный элемент  является единственным.
является единственным.
2.  для любого
для любого  .
.
3. Для любого  противоположный элемент
противоположный элемент  является единственным. 4.
является единственным. 4. 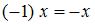 для любого
для любого  .
.
5.  для любых
для любых  и
и  .
.
 ЗАДАНИЕ N 31 сообщить об ошибке
ЗАДАНИЕ N 31 сообщить об ошибке
Тема: Обратная матрица
Для матрицы  существует обратная, если она равна …
существует обратная, если она равна …

 ЗАДАНИЕ N 32 сообщить об ошибке
ЗАДАНИЕ N 32 сообщить об ошибке
Тема: Линейные операции над матрицами
Даны матрицы  ,
,  . Тогда матрица
. Тогда матрица  равна …
равна …

Преподаватель: Базайкина О.Л.
Специальность: 080104.65 - Экономика труда
Группа: ЭЭТ-091 Дисциплина: Математика
Идентификатор студента: Кремнева Е.
Логин: 05ps36350
Начало тестирования: 2012-03-11 10:48:16 Завершение тестирования: 2012-03-11 11:35:21 Продолжительность тестирования: 47 мин. Заданий в тесте: 32 Кол-во правильно выполненных заданий: 16
Процент правильно выполненных заданий: 50 %

 ЗАДАНИЕ N 1 сообщить об ошибке
ЗАДАНИЕ N 1 сообщить об ошибке
Тема: Теоремы сложения и умножения вероятностей
Наладчик обслуживает три станка. Вероятность того, что в течение часа потребует его вмешательства первый станок, равна  ; второй –
; второй –  ; третий
; третий
–  . Тогда вероятность того, что в течение часа потребует вмешательства наладчика хотя бы один станок, равна …
. Тогда вероятность того, что в течение часа потребует вмешательства наладчика хотя бы один станок, равна …
0,49
0,51
0,6
0,25
Решение:
Введем обозначения событий: (вмешательства наладчика потребует
(вмешательства наладчика потребует  – ый
– ый
станок),  (вмешательства наладчика потребует хотя бы один станок). Тогда
(вмешательства наладчика потребует хотя бы один станок). Тогда
.

 ЗАДАНИЕ N 2 сообщить об ошибке
ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Числовые характеристики случайных величин
Дискретная случайная величина X задана законом распределения вероятностей:
Тогда ее дисперсия равна …
7,56
3,2
3,36



 ЗАДАНИЕ N 6 сообщить об ошибке
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Системы линейных уравнений
Фундаментальное решение может быть вычислено для системы вида …
Решение:
Фундаментальное решение может быть вычислено для однородной системы линейных алгебраических уравнений. Однородной системой линейных алгебраических уравнений называется система, все свободные члены которой
равны нулю, например, система 

 ЗАДАНИЕ N 7 сообщить об ошибке
ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Обратная матрица
Для матрицы  существует обратная, если ее определитель …
существует обратная, если ее определитель …
=0

 ЗАДАНИЕ N 8 сообщить об ошибке
ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Определение линейного пространства
Аксиомой линейного пространства  является …
является …
 ,
, 
 ;
; 
 ,
, 
 ;
; 

 ЗАДАНИЕ N 9 сообщить об ошибке
ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Ранг матрицы
Ранг матрицы  равен двум, если значение
равен двум, если значение  не равно …
не равно …
– 1 0
– 2 1
Решение:
Рангом матрицы называется наибольший из порядков ее миноров, не равных нулю. Следовательно, если минор второго порядка не равен нулю, то ранг будет
равен двум. Вычислим  . То есть
. То есть  .
.
 ЗАДАНИЕ N 10 сообщить об ошибке
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Линейные операции над матрицами
Даны матрицы  ,
,  . Тогда матрица
. Тогда матрица  равна …
равна …


 ЗАДАНИЕ N 11 сообщить об ошибке
ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Асимптоты графика функции
Горизонтальная асимптота графика функции  задается уравнением вида …
задается уравнением вида …
Решение:
Прямая  является горизонтальной асимптотой графика функции
является горизонтальной асимптотой графика функции 
при  (
( ) если существует
) если существует  (
( ). Вычислив предел
). Вычислив предел
 ,
,
получаем уравнение горизонтальной асимптоты  .
.
 ЗАДАНИЕ N 12 сообщить об ошибке
ЗАДАНИЕ N 12 сообщить об ошибке
Тема: Дифференциальное исчисление ФНП
Частная производная  функции
функции  имеет вид …
имеет вид …

 будет …
будет …

 . Значит, ранг расширенной матрицы равен рангу основной матрицы и система будет совместной. Так как количество переменных больше ранга матрицы, система имеет бесконечное число решений, а значит, является неопределенной.
. Значит, ранг расширенной матрицы равен рангу основной матрицы и система будет совместной. Так как количество переменных больше ранга матрицы, система имеет бесконечное число решений, а значит, является неопределенной.


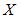 можно вычислить по формуле
можно вычислить по формуле . Тогда
. Тогда

 задана законом распределения вероятностей:
задана законом распределения вероятностей:



 равен …
равен …