
3
.pdf
 .
.
Следовательно, прямая  будет вертикальной асимптотой.
будет вертикальной асимптотой.

 ЗАДАНИЕ N 3 сообщить об ошибке
ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Приложения дифференциального исчисления ФОП
Промежуток убывания функции  имеет вид …
имеет вид …

 ЗАДАНИЕ N 4 сообщить об ошибке
ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Предел функции
Предел  равен …
равен …

1
Решение:
Разложим числитель и знаменатель на линейные множители как  и
и  .
.
.

 ЗАДАНИЕ N 5 сообщить об ошибке
ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Основные методы интегрирования
Множество первообразных функции  имеет вид …
имеет вид …

Решение:
Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции. Тогда
Произведем замену  ,
,  ,
,  :
:
.

 ЗАДАНИЕ N 6 сообщить об ошибке
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Область определения функции
Область определения функции  имеет вид …
имеет вид …

Решение:
Область определения данной логарифмической функции определяется как решение системы неравенств:
то есть |
. |

 ЗАДАНИЕ N 7 сообщить об ошибке
ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Производные первого порядка
Производная функции 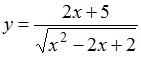 равна …
равна …
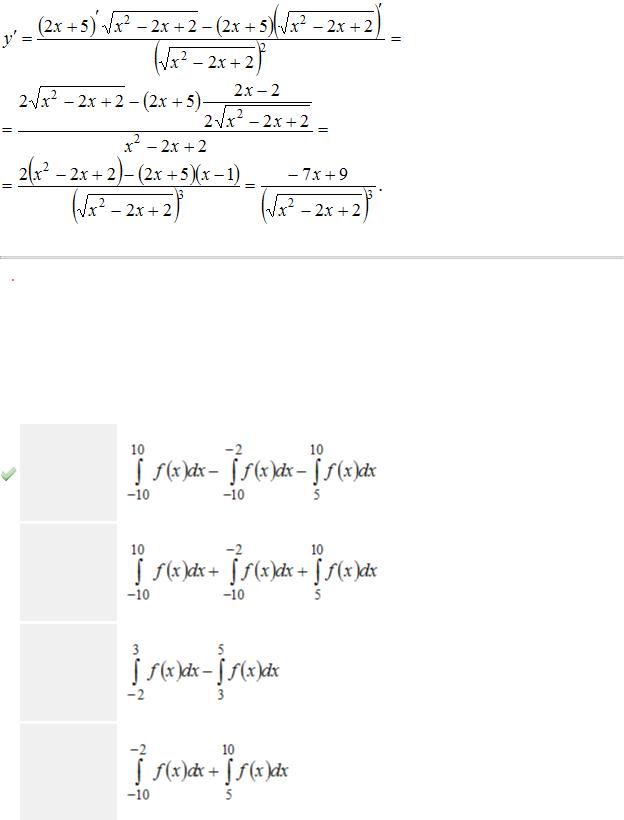
Решение:

 ЗАДАНИЕ N 8 сообщить об ошибке
ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Свойства определенного интеграла
Если функция  непрерывна на отрезке
непрерывна на отрезке  , то интеграл
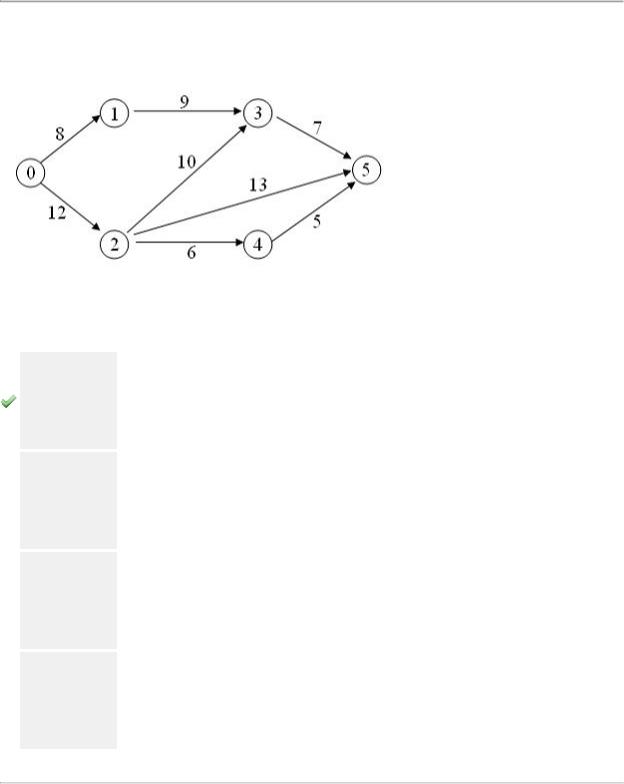
, то интеграл  можно представить в виде …
можно представить в виде …
Решение:
Если функция  непрерывна на отрезке
непрерывна на отрезке  и
и  , то справедливо следующее свойство определенного интеграла:
, то справедливо следующее свойство определенного интеграла:
 .
.
Тогда  .
.
 ЗАДАНИЕ N 9 сообщить об ошибке
ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Сетевое планирование и управление
Сетевой график изображен на рисунке
Тогда, для изменения критического пути, продолжительность работы  можно увеличить на …
можно увеличить на …
7 дней
5 дней
3 дня
1 день
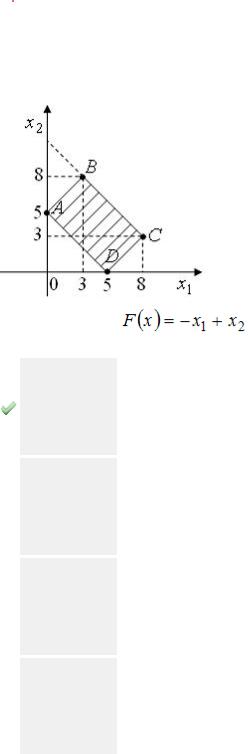

 ЗАДАНИЕ N 10 сообщить об ошибке
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Линейное программирование: графическое задание области допустимых решений
Область допустимых решений ABCD задачи линейного программирования имеет вид:
Тогда функция |
достигает минимального значения … |
на отрезке CD
на отрезке AB
только в точке D
в точке B
Решение:
Построим линию уровня  и градиент целевой функции
и градиент целевой функции
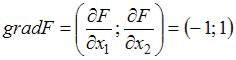 . Тогда целевая функция будет принимать наименьшее значение в точках «входа» линии уровня в область допустимых решений в направлении градиента.
. Тогда целевая функция будет принимать наименьшее значение в точках «входа» линии уровня в область допустимых решений в направлении градиента.
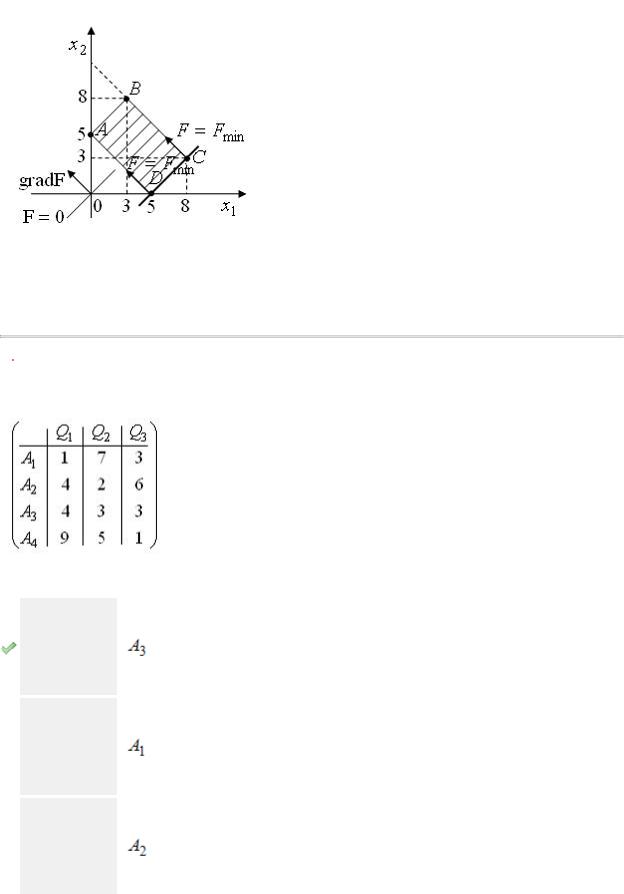
Из рисунка видно, что точки минимума будут лежать на отрезке  как на
как на
точках «входа» линии уровня 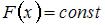 в область допустимых решений в направлении градиента.
в область допустимых решений в направлении градиента.

 ЗАДАНИЕ N 11 сообщить об ошибке
ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Теория игр: игры с природой
Матрица выигрышей в игре с природой имеет вид:
Тогда оптимальной по критерию Вальда будет стратегия …
Решение:
По критерию Вальда оптимальной является стратегия, которой соответствует максимальный из минимальных выигрышей, то есть
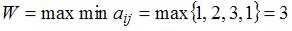 . Следовательно, оптимальной по критерию Вальда будет стратегия
. Следовательно, оптимальной по критерию Вальда будет стратегия  .
.

 ЗАДАНИЕ N 12 сообщить об ошибке
ЗАДАНИЕ N 12 сообщить об ошибке
Тема: Транспортная задача
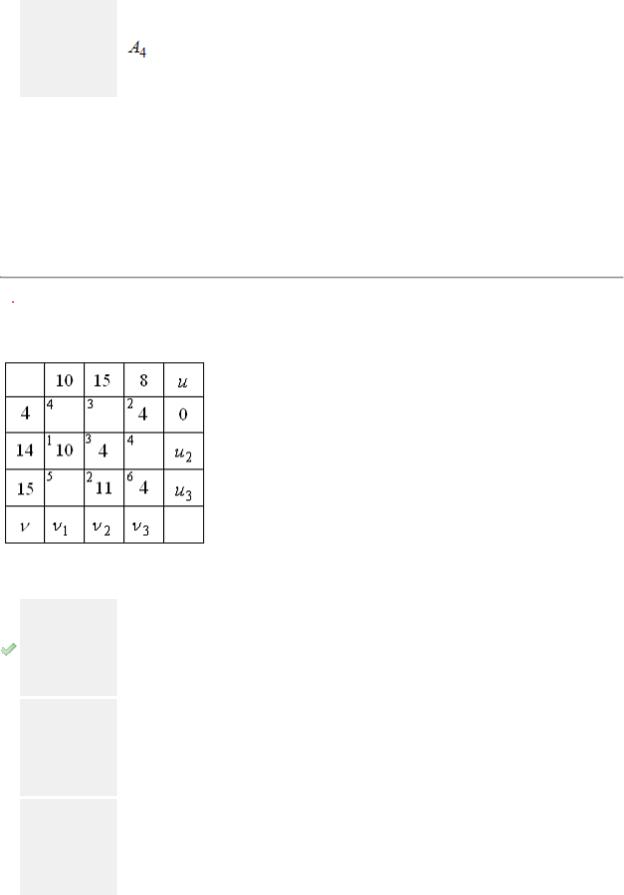
В транспортной задаче распределение поставок задано таблицей:
Тогда значение потенциала  будет равно …
будет равно …
– 2
0
2

4
Решение:
Сумма потенциалов для занятых клеток должна быть равна тарифу. Следовательно,  , то есть
, то есть  .
.  , то есть
, то есть  .
.
 , то есть
, то есть  .
.

 ЗАДАНИЕ N 13 сообщить об ошибке
ЗАДАНИЕ N 13 сообщить об ошибке
Тема: Производственные функции
Задана производственная функция  . Тогда предельный продукт капитала при
. Тогда предельный продукт капитала при 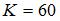 ,
,  равен …
равен …
Решение:
Предельный продукт капитала вычисляется по формуле 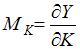 . Тогда
. Тогда
