Функция полезности не обладает свойством  , так как при очень большом объеме блага его дальнейшее увеличение не приводит к увеличению полезности, то есть
, так как при очень большом объеме блага его дальнейшее увеличение не приводит к увеличению полезности, то есть
.
А так как с ростом объема потребления блага скорость роста полезности замедляется, то функция полезности обладает свойством  .
.
 ЗАДАНИЕ N 15 сообщить об ошибке
ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Предел функции
Предел  равен :
равен :
3
1
0
Решение:
Данный предел можно вычислить с использованием первого замечательного предела и его следствий вида  и
и  , а именно:
, а именно:
 ЗАДАНИЕ N 16 сообщить об ошибке
ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Основные методы интегрирования
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511532[11.05.2012 0:00:44]
Множество первообразных функции 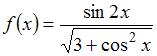 имеет вид :
имеет вид :
 ЗАДАНИЕ N 17 сообщить об ошибке
ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Область определения функции
Область определения функции  имеет вид :
имеет вид :
Решение:
Данная функция определена, если подкоренное выражение в числителе неотрицательно, а знаменатель не равен нулю. Тогда
Следовательно, получаем, что  .
.
ЗАДАНИЕ N 18 сообщить об ошибке |
|
Тема: Приложения дифференциального исчисления ФОП |
|
Уравнение касательной к графику функции |
в его точке с абсциссой |
имеет вид : |
|
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511532[11.05.2012 0:00:44]
ЗАДАНИЕ N 19 сообщить об ошибке |
|
Тема: Производные первого порядка |
|
Функция |
задана в параметрическом виде |
Тогда производная первого |
порядка функции |
по переменной имеет вид : |
|
Решение:
.
ЗАДАНИЕ N 20 сообщить об ошибке |
|
|
Тема: Дифференциальное исчисление ФНП |
|
|
Приближенное значение функции |
в точке |
, |
вычисленное с помощью полного дифференциала, равно : |
|
|
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511532[11.05.2012 0:00:44]
Решение:
Воспользуемся формулой |
|
, |
где |
, |
, |
, |
. |
Вычислим последовательно |
; |
|
|
|
|
|
|
|
|
, |
; |
|
|
|
, |
. |
Тогда |
|
|
|
. |
|
|
|
|
 ЗАДАНИЕ N 21 сообщить об ошибке
ЗАДАНИЕ N 21 сообщить об ошибке
Тема: Асимптоты графика функции
Наклонная асимптота графика функции  задается уравнением вида :
задается уравнением вида :
Решение:
Прямая |
является наклонной асимптотой графика функции |
при |
( |
|
), если существуют конечные пределы: |
|
|
,  , или соответственно
, или соответственно
,  .
.
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511532[11.05.2012 0:00:44]
|
|
. |
Следовательно, прямая |
|
является наклонной асимптотой графика данной |
функции как при |
, так и при |
. |
 ЗАДАНИЕ N 22 сообщить об ошибке
ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Свойства определенного интеграла
Значение определенного интеграла |
принадлежит промежутку : |
 ЗАДАНИЕ N 23 сообщить об ошибке
ЗАДАНИЕ N 23 сообщить об ошибке
Тема: Точечные оценки параметров распределения
Проведено пять измерений (без систематических ошибок) некоторой случайной величины (в мм): 4,5; 5,2; 6,1; 7,8, 8,3. Тогда несмещенная оценка математического ожидания равна :
6,38
6,42
6,1
6,4
 ЗАДАНИЕ N 24 сообщить об ошибке
ЗАДАНИЕ N 24 сообщить об ошибке
Тема: Характеристики вариационного ряда
Медиана вариационного ряда 5, 7, 9, 12, 12, 15, 16, 17, 18, 19, 21 равна :
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511532[11.05.2012 0:00:44]
15
12
16
13
 ЗАДАНИЕ N 25 сообщить об ошибке
ЗАДАНИЕ N 25 сообщить об ошибке
Тема: Интервальные оценки параметров распределения
Точечная оценка вероятности биномиально распределенного количественного признака равна 0,38. Тогда его интервальная оценка может иметь вид :
Решение:
Интервальная оценка |
вероятности биномиально распределенного количественного |
признака симметрична относительно его точечной оценки, и |
. Таким свойствам |
удовлетворяет интервал |
. |
|
 ЗАДАНИЕ N 26 сообщить об ошибке
ЗАДАНИЕ N 26 сообщить об ошибке
Тема: Проверка статистических гипотез
Соотношением вида  можно определить :
можно определить :

 двустороннюю критическую область
двустороннюю критическую область
 правостороннюю критическую область
правостороннюю критическую область
 левостороннюю критическую область
левостороннюю критическую область  область принятия гипотезы
область принятия гипотезы
ЗАДАНИЕ N 27 сообщить об ошибке |
|
|
Тема: Элементы корреляционного анализа |
|
|
Выборочное уравнение прямой линии регрессии |
на имеет вид |
. |
Тогда выборочное среднее признака равно : |
|
|
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511532[11.05.2012 0:00:44]
ЗАДАНИЕ N 28 сообщить об ошибке |
|
Тема: Статистическое распределение выборки |
|
Из генеральной совокупности извлечена выборка объема |
, полигон частот которой имеет |
вид: |
|
Тогда относительная частота варианты  в выборке равна :
в выборке равна :
0,05
0,06
0,25
0,20
Решение:
Относительная частота 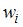 вычисляется по формуле
вычисляется по формуле  , где
, где  - частота варианты
- частота варианты  , а
, а  - объем выборки. Вычислим предварительно частоту варианты
- объем выборки. Вычислим предварительно частоту варианты  как
как
 . Тогда
. Тогда  .
.
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511532[11.05.2012 0:00:44]
 ЗАДАНИЕ N 29 сообщить об ошибке
ЗАДАНИЕ N 29 сообщить об ошибке
Тема: Линейное программирование: графическое задание области допустимых решений
Область допустимых решений OABC задачи линейного программирования имеет вид:
Тогда максимальное значение функции  достигается в точке :
достигается в точке :
B
D
A
C
 ЗАДАНИЕ N 30 сообщить об ошибке
ЗАДАНИЕ N 30 сообщить об ошибке
Тема: Сетевое планирование и управление
Сетевой график изображен на рисунке
Тогда полный резерв времени работы  равен :
равен :
0
4
34
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511532[11.05.2012 0:00:44]
20
 ЗАДАНИЕ N 31 сообщить об ошибке
ЗАДАНИЕ N 31 сообщить об ошибке
Тема: Транспортная задача
В транспортной задаче первоначальное распределение поставок имеет вид:
Тогда на следующем шаге необходимо осуществить поставку в клетку с номером :
 решение оптимальное, перераспределение поставок осуществлять не надо
решение оптимальное, перераспределение поставок осуществлять не надо
Решение:
При перераспределении поставок поставка осуществляется в свободную клетку, для которой
сумма потенциалов будет больше соответствующего тарифа, то есть |
. |
Следовательно, поставку осуществляем в клетку с номером |
, так как для нее |
|
. |
|
|
 ЗАДАНИЕ N 32 сообщить об ошибке
ЗАДАНИЕ N 32 сообщить об ошибке
Тема: Теория игр: игры с природой
Матрица выигрышей в игре с природой имеет вид:
Тогда оптимальной по критерию Вальда будет стратегия :
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511532[11.05.2012 0:00:44]
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511532[11.05.2012 0:00:44]








 в выборке равна :
в выборке равна :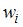 вычисляется по формуле
вычисляется по формуле  , где
, где  - частота варианты
- частота варианты  , а
, а  - объем выборки. Вычислим предварительно частоту варианты
- объем выборки. Вычислим предварительно частоту варианты  как
как . Тогда
. Тогда  .
.



 , так как при очень большом объеме блага его дальнейшее увеличение не приводит к увеличению полезности, то есть
, так как при очень большом объеме блага его дальнейшее увеличение не приводит к увеличению полезности, то есть .
.
 равен :
равен : и
и 

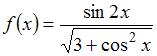 имеет вид :
имеет вид :
 имеет вид :
имеет вид : .
.
 задается уравнением вида :
задается уравнением вида : , или соответственно
, или соответственно .
.




 можно определить :
можно определить :
 двустороннюю критическую область
двустороннюю критическую область правостороннюю критическую область
правостороннюю критическую область левостороннюю критическую область
левостороннюю критическую область  область принятия гипотезы
область принятия гипотезы
 достигается в точке :
достигается в точке :
 равен :
равен :
 решение оптимальное, перераспределение поставок осуществлять не надо
решение оптимальное, перераспределение поставок осуществлять не надо