 ЗАДАНИЕ N 9 сообщить об ошибке
ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Производные первого порядка
Неявная функция  определяется как решение уравнения
определяется как решение уравнения  . Тогда производная первого порядка
. Тогда производная первого порядка  при
при  равна :
равна :
0
1
Решение:
Продифференцируем по обе части уравнения |
. |
Тогда |
|
.
Решим последнее уравнение относительно  , получаем
, получаем
.
Подставив значение 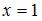 в уравнение
в уравнение  , получаем
, получаем  , то есть
, то есть  . Тогда
. Тогда  .
.
 ЗАДАНИЕ N 10 сообщить об ошибке
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Асимптоты графика функции
Вертикальная асимптота графика функции  задается уравнением вида :
задается уравнением вида :
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511531[10.05.2012 23:59:22]
 ЗАДАНИЕ N 11 сообщить об ошибке
ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Предел функции
Предел  равен :
равен :
0
1
 ЗАДАНИЕ N 12 сообщить об ошибке
ЗАДАНИЕ N 12 сообщить об ошибке
Тема: Приложения дифференциального исчисления ФОП
Наименьшее значение функции на отрезке
на отрезке  равно :
равно :
Решение:
Вычислим производную первого порядка |
и решим уравнение |
, а |
именно |
. Тогда |
, |
. Так как |
, |
то вычислим |
|
|
|
|
, |
|
, |
. |
|
Тогда наименьшее значение данной функции равно  .
.
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511531[10.05.2012 23:59:22]
 ЗАДАНИЕ N 13 сообщить об ошибке
ЗАДАНИЕ N 13 сообщить об ошибке
Тема: Свойства определенного интеграла
Функция задана и непрерывна на всей числовой прямой, и  - действительные числа. Тогда верно утверждение :
- действительные числа. Тогда верно утверждение :
Решение:
Если функция задана и непрерывна на всей числовой прямой, и ,  , - действительные числа, то справедливо следующее свойство определенного интеграла:
, - действительные числа, то справедливо следующее свойство определенного интеграла:
|
, |
или |
. Тогда, например, при |
|
. |
 ЗАДАНИЕ N 14 сообщить об ошибке
ЗАДАНИЕ N 14 сообщить об ошибке
Тема: Дифференциальное исчисление ФНП
Полный дифференциал функции  имеет вид :
имеет вид :
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511531[10.05.2012 23:59:22]
Решение:
Полный дифференциал функции нескольких переменных равен сумме произведений частных производных этой функции на дифференциалы соответствующих независимых переменных, то есть
.
Тогда
 ЗАДАНИЕ N 15 сообщить об ошибке
ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Основные методы интегрирования
Множество первообразных функции  имеет вид :
имеет вид :
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511531[10.05.2012 23:59:22]
ЗАДАНИЕ N 16 сообщить об ошибке |
|
|
Тема: Область определения функции |
|
|
Область определения функции |
содержит интервал |
. Тогда значение |
параметра может быть равно : |
|
|
0,5
2
1
0
 ЗАДАНИЕ N 17 сообщить об ошибке
ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Проверка статистических гипотез
Основная гипотеза имеет вид  . Тогда конкурирующей может являться гипотеза :
. Тогда конкурирующей может являться гипотеза :
 ЗАДАНИЕ N 18 сообщить об ошибке
ЗАДАНИЕ N 18 сообщить об ошибке
Тема: Статистическое распределение выборки
Из генеральной совокупности извлечена выборка объема  :
:
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511531[10.05.2012 23:59:22]
Тогда частота варианты  в выборке равна :
в выборке равна :
28
63
42
35
 ЗАДАНИЕ N 19 сообщить об ошибке
ЗАДАНИЕ N 19 сообщить об ошибке
Тема: Точечные оценки параметров распределения
В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 15; 18; 21; 24. Тогда выборочная дисперсия равна :
11,25
19,5
15
21,25
 ЗАДАНИЕ N 20 сообщить об ошибке
ЗАДАНИЕ N 20 сообщить об ошибке
Тема: Интервальные оценки параметров распределения
Точечная оценка среднего квадратического отклонения нормально распределенного количественного признака равна 3,5. Тогда его интервальная оценка может иметь вид :
Решение:
Интервальной оценкой среднего квадратического отклонения нормально распределенного количественного признака служит доверительный интервал
|
при |
|
или |
при |
, где q находят по соответствующей таблице приложений. |
Этому определению удовлетворяет интервал  .
.
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511531[10.05.2012 23:59:22]
 ЗАДАНИЕ N 21 сообщить об ошибке
ЗАДАНИЕ N 21 сообщить об ошибке
Тема: Характеристики вариационного ряда
Медиана вариационного ряда 5, 7, 9, 12, 12, 15, 16, 17, 18, 19, 21 равна :
15
12
16
13
ЗАДАНИЕ N 22 сообщить об ошибке |
|
|
Тема: Элементы корреляционного анализа |
|
|
Выборочное уравнение прямой линии регрессии |
на имеет вид |
. |
Тогда выборочное среднее признака равно : |
|
|
Решение:
Выборочное уравнение прямой линии регрессии |
на имеет вид |
. Тогда |
выборочное среднее признака равно |
. |
|
|
 ЗАДАНИЕ N 23 сообщить об ошибке
ЗАДАНИЕ N 23 сообщить об ошибке
Тема: Обратная матрица
Для матрицы |
не существует обратной, если значение равно : |
2 - 2 1 - 1
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511531[10.05.2012 23:59:22]
 ЗАДАНИЕ N 24 сообщить об ошибке
ЗАДАНИЕ N 24 сообщить об ошибке
Тема: Определение линейного пространства
Аксиомой линейного пространства  не является :
не является :
 ,
, 
 ,
, 
 ,
, 
 ,
, 
 ЗАДАНИЕ N 25 сообщить об ошибке
ЗАДАНИЕ N 25 сообщить об ошибке
Тема: Вычисление определителей
Разложение определителя |
по строке может иметь вид : |
 ЗАДАНИЕ N 26 сообщить об ошибке
ЗАДАНИЕ N 26 сообщить об ошибке
Тема: Системы линейных уравнений
Базисное решение системы  может иметь вид :
может иметь вид :
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511531[10.05.2012 23:59:22]
 ЗАДАНИЕ N 27 сообщить об ошибке
ЗАДАНИЕ N 27 сообщить об ошибке
Тема: Линейные операции над матрицами |
|
Даны матрицы |
и |
. Тогда решением уравнения |
является матрица |
, равная : |
|
 ЗАДАНИЕ N 28 сообщить об ошибке
ЗАДАНИЕ N 28 сообщить об ошибке
Тема: Ранг матрицы
Ранг матрицы  равен :
равен :
2
1
3
4
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511531[10.05.2012 23:59:22]
Решение:
Рангом матрицы называется наибольший из порядков ее миноров, не равных нулю. Так как существуют ненулевые миноры второго порядка, например
, то ранг матрицы равен двум.
 ЗАДАНИЕ N 29 сообщить об ошибке
ЗАДАНИЕ N 29 сообщить об ошибке
Тема: Определение вероятности
Из урны, в которой находятся 6 черных шаров и 4 белых шара, вынимают одновременно 3 шара. Тогда вероятность того, что среди отобранных два шара будут черными, равна :
 ЗАДАНИЕ N 30 сообщить об ошибке
ЗАДАНИЕ N 30 сообщить об ошибке
Тема: Законы распределения вероятностей дискретных случайных величин
Дискретная случайная величина |
задана законом распределения вероятностей: |
Тогда ее функция распределения вероятностей имеет вид :
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps511531[10.05.2012 23:59:22]





 ЗАДАНИЕ N 15 сообщить об ошибке
ЗАДАНИЕ N 15 сообщить об ошибке имеет вид :
имеет вид :
 ЗАДАНИЕ N 17 сообщить об ошибке
ЗАДАНИЕ N 17 сообщить об ошибке . Тогда конкурирующей может являться гипотеза :
. Тогда конкурирующей может являться гипотеза : ЗАДАНИЕ N 18 сообщить об ошибке
ЗАДАНИЕ N 18 сообщить об ошибке :
:



 ЗАДАНИЕ N 27 сообщить об ошибке
ЗАДАНИЕ N 27 сообщить об ошибке ЗАДАНИЕ N 28 сообщить об ошибке
ЗАДАНИЕ N 28 сообщить об ошибке равен :
равен :


 определяется как решение уравнения
определяется как решение уравнения  . Тогда производная первого порядка
. Тогда производная первого порядка  при
при  равна :
равна : , получаем
, получаем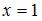 в уравнение
в уравнение  , получаем
, получаем  , то есть
, то есть  . Тогда
. Тогда  .
.
 задается уравнением вида :
задается уравнением вида :
 равен :
равен :
 на отрезке
на отрезке  равно :
равно : .
.
 - действительные числа. Тогда верно утверждение :
- действительные числа. Тогда верно утверждение : , - действительные числа, то справедливо следующее свойство определенного интеграла:
, - действительные числа, то справедливо следующее свойство определенного интеграла:
 имеет вид :
имеет вид : в выборке равна :
в выборке равна :

 .
.



 ,
, 
 ,
, 
 ,
, 
 ,
, 


 может иметь вид :
может иметь вид :
